Dynamique des systèmes - Système premier ordre

[invite20e071f3]

Bonjour à tous,

Je suis entrain de résoudre un exercice et j'aimerais avoir un avis sur la réponse que j'obtiens car je ne suis pas certain de mon raisonement.

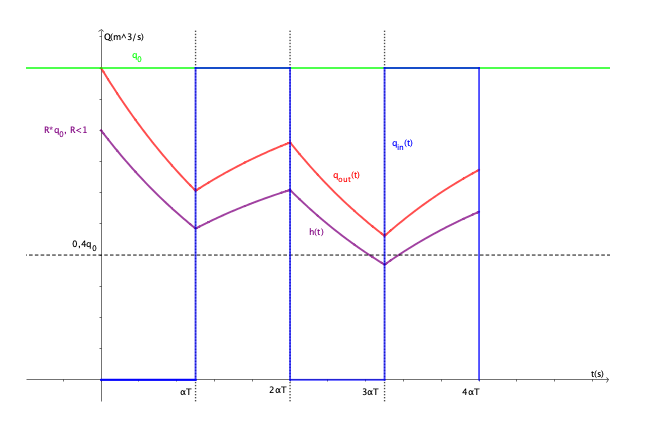
Il s'agit d'un reservoir ayant un débit sortant et un débit entrant. Le débit entrant est nul entre 0<t<T puis vaut q0 entre T<t<2T puis nul entre 2T<t<3T, .... Le but de l'exercice est de trouver l'expression du débit sortant et de tracer le graph.

Ce système est représenter par l'equation suivante : où tho = AR et K =R

Et le débit sortant vaut .

Si il n'y a pas de débit entrant, la solution de l'equation est
Si le débit entrant vaut q0, la solution est

avec comme condition initiale : h(0) = q0*R

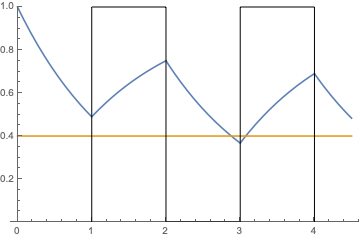
Pour résoudre cet exercice, j'ai résolu l'équation différentielle par intervalle en utilisant les conditions finales de l'intervalle 0<t<T comme conditions initiales de l'intervalle suivant, et ainsi de suite. J'obtiens alors une evolution de ce type :



Je pense que mon raisonnement tient la route. En revanche, je me demande si il n'y a pas un moyen plus rapide pour trouver la réponse.
Si vous avez une meilleure idée, je serais intéressé de la connaitre.

Bonne journée à tous,
Merci d'avance pour votre aide.
-----

[stefjm]

Salut,
Ca se fait en 4 lignes de calcul par transformée de Laplace.


Premier ordre entre débit entrant et h.
Constante entre h et débit sortant.

Il suffit d'utiliser l'échelon de Heaviside (et ses retardés), de transformer en Laplace, de multiplier par les fonction de transfert et de revenir à l'original temporel.

1)


2) TL en utilisant le th du retard. https://fr.wikipedia.org/wiki/Transf...ion_de_Laplace

3)
Multiplication de q par mla fonction de transfert

4) retour à l'original

On peut même faire plus joli en utilisant la TL de fonction périodique.

[invite20e071f3]

Bonjour,

Merci pour votre réponse.

Donc à l'étape 2, j'aurais :

A l'étape 3 :

Et il me reste à revenir en temporel avec la transformée inverse ?

[invite20e071f3]

A l'étape 4 :



Je dois avoir une erreur parce que si t<T, mon débit sera nul si je comprends bien mon expression. Je ne trouve pas mon erreur

[A voir en vidéo sur Futura]

[stefjm]

Il n'y a pas d'erreur (ou du moins pas d'évidentes)!

Les fonction de transfert en Laplace ne permet pas de gerer la condition initiale non nulle ou les composantes continues.
Il faut le faire après coup.

[invite20e071f3]

On fait comment pour obtenir les conditions initiales ? Puisque je n'ai plus les constantes d'intégration provenant de l'équation différentielle.
En fait je voulais une autre méthode afin de pouvoir vérifier mes résultats et mon évolution tempo de q_out car je ne suis pas sûr de mes calculs.

[gts2]

Pourquoi des conditions initiales, il n'y en a qu'une : h=h0.

Il faut juste traiter la première demi période à part : qui donne soit

Et cela donne bien les courbes que vous avez donné.

[gts2]

On peut d'ailleurs tout regrouper ...

[stefjm]

Oui, et pour le faire élégamment avec la TL, il suffit voir que la condition initiale non nulle du premier ordre correspond à la réponse à une impulsion de Dirac en t=0.

[invite20e071f3]

Merci à tous

[invite20e071f3]

Excusez moi pour cette question mais

Avec la condition initiale, j'obtiens

Ensuite vous me dites que je peux tout regrouper ensemble, mais je ne vois pas comment faire

[gts2]

Soir en Laplace : qui donne soit

Soit en s'inspirant de Laplace pour résoudre en temporel : vous avez une suite d'échelons +q₀ à (2n-1)T (n=1..) et -q₀ à 2nT de solution kq₀(1-exp(..)) et kq₀(-1+exp(...))
Il suffit d'ajouter toutes ces solutions (linéarité), avec le décalage temporel adéquat à h₀ exp(...) pour avoir la solution.

[invite20e071f3]

Comme ceci ?

[gts2]

Oui, c'est bien cela et cela donne graphiquement :

[gts2]

En Laplace : qui donne soit

Ou pour reprendre la suggestion de @stejm qui conduit (heureusement !) à la même chose

D'où détection d'une faute de parenthèses dans mon expression initiale ! soit

[invite20e071f3]

Super merci beaucoup

[stefjm]

<HS>
3 forumeurs qui font de la transformée de Laplace sur le même fil de FSG, c'est du jamais vu!