Je ne comprends pas la phrase. Notamment en gras...Oui, et si tu changes de métrique comme expliqué plus haut, la mesure des longueurs se fait sur les mêmes évènements, ça devient juste une question de perception des longueurs par la perspective, et c'est géométriquement représentable.
De plus, il est aussi toujours question de perception, perceptive et c'est géométriquement représentable.
Sinon on obtient quoi comme longueur en procédant ainsi ?
-----




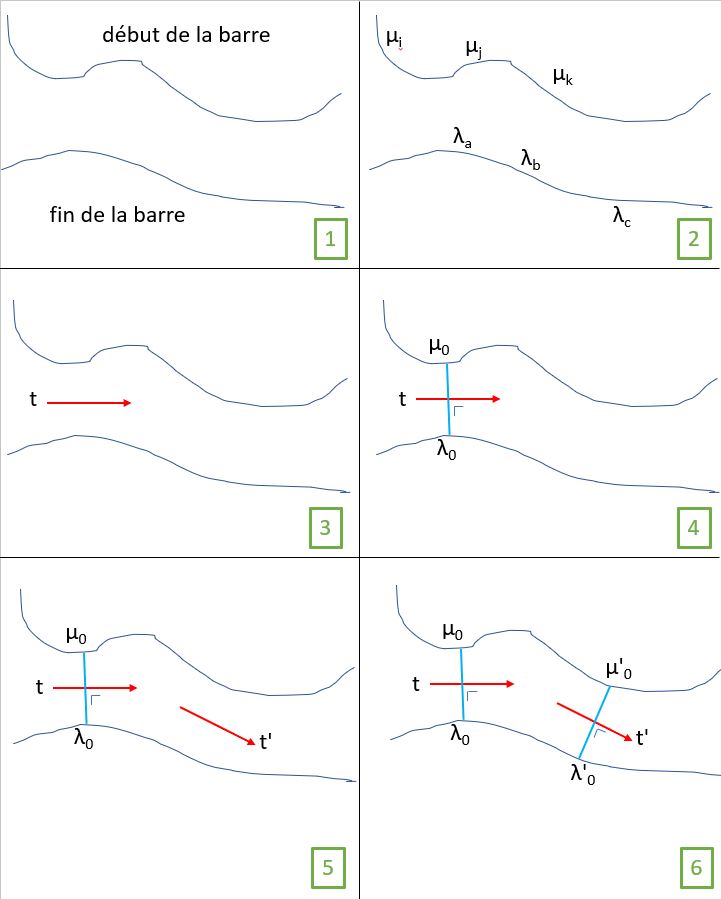
 ,
, 
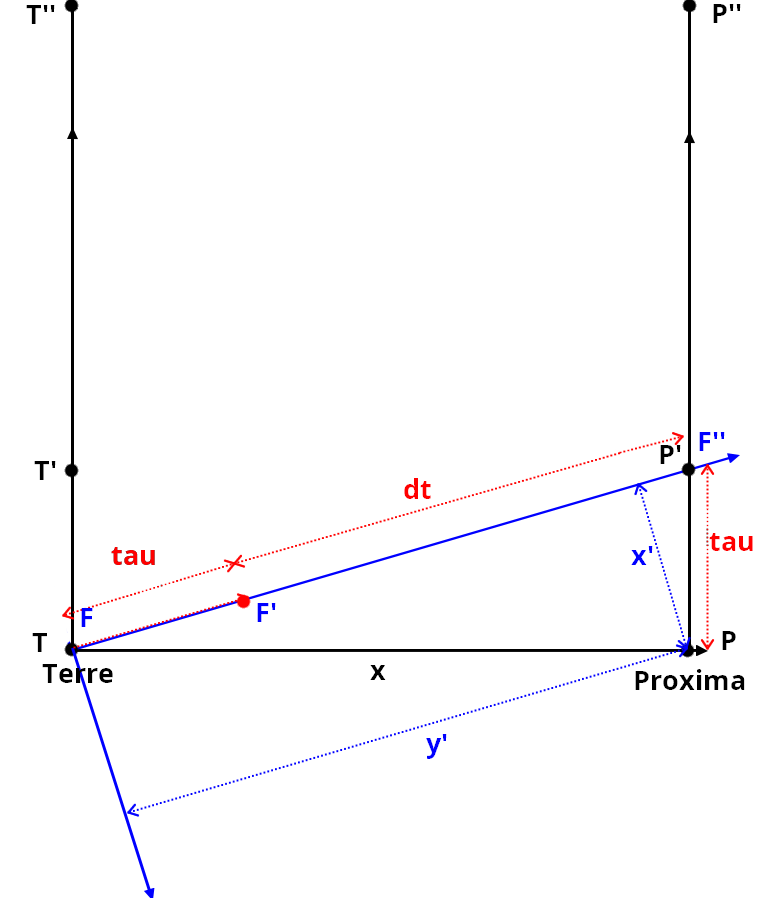
 T'es sympa toi, tu me rend responsable de tes c.. ! Mais allons y, ça ne va pas te plaire, je ne peux défendre que ce qui est défendable.
T'es sympa toi, tu me rend responsable de tes c.. ! Mais allons y, ça ne va pas te plaire, je ne peux défendre que ce qui est défendable.