Bonjour.
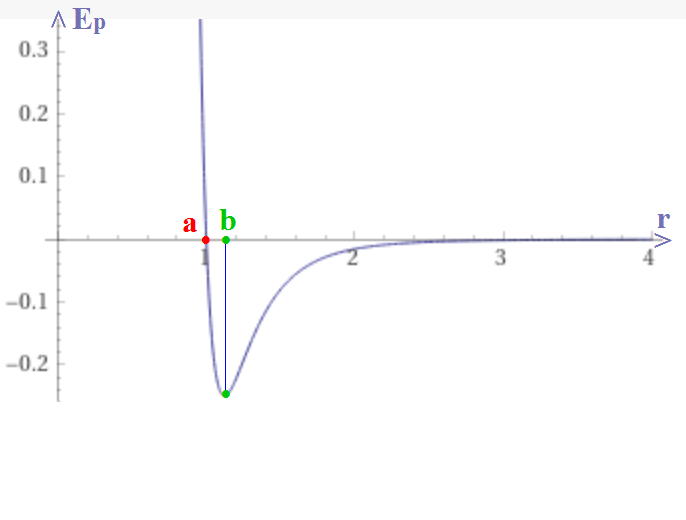
Voila j'éssaye de visualiser les interractions entre les molécule d'un liquide mais je n'arrive pas à comprendre comment il peut être déformable et incompressible à la fois.
S'il est incompressible, c'est à dire qu'il résiste à la compression et à la décompréssion. C'est comme si les particule étaient attachée entre elles par des petites barres solide de sorte qu'elles soient forcé de rester à la meme distance les unes des autres.
Dans la vraie vie une structure faite de barres reliée entre elles est très solide et indéformable comme par exemple la mat d'une grue.
Si quelqu'un arrivait a me donner un exemple visuel pour m'expliquer comment on peut obtenir une structure résistance à la pression et molle en meme temps... ?
-----