Question sur une représentation en relativité restreinte.

[jlthirot]

Donc, est-ce possible de faire le raisonnement suivant ?

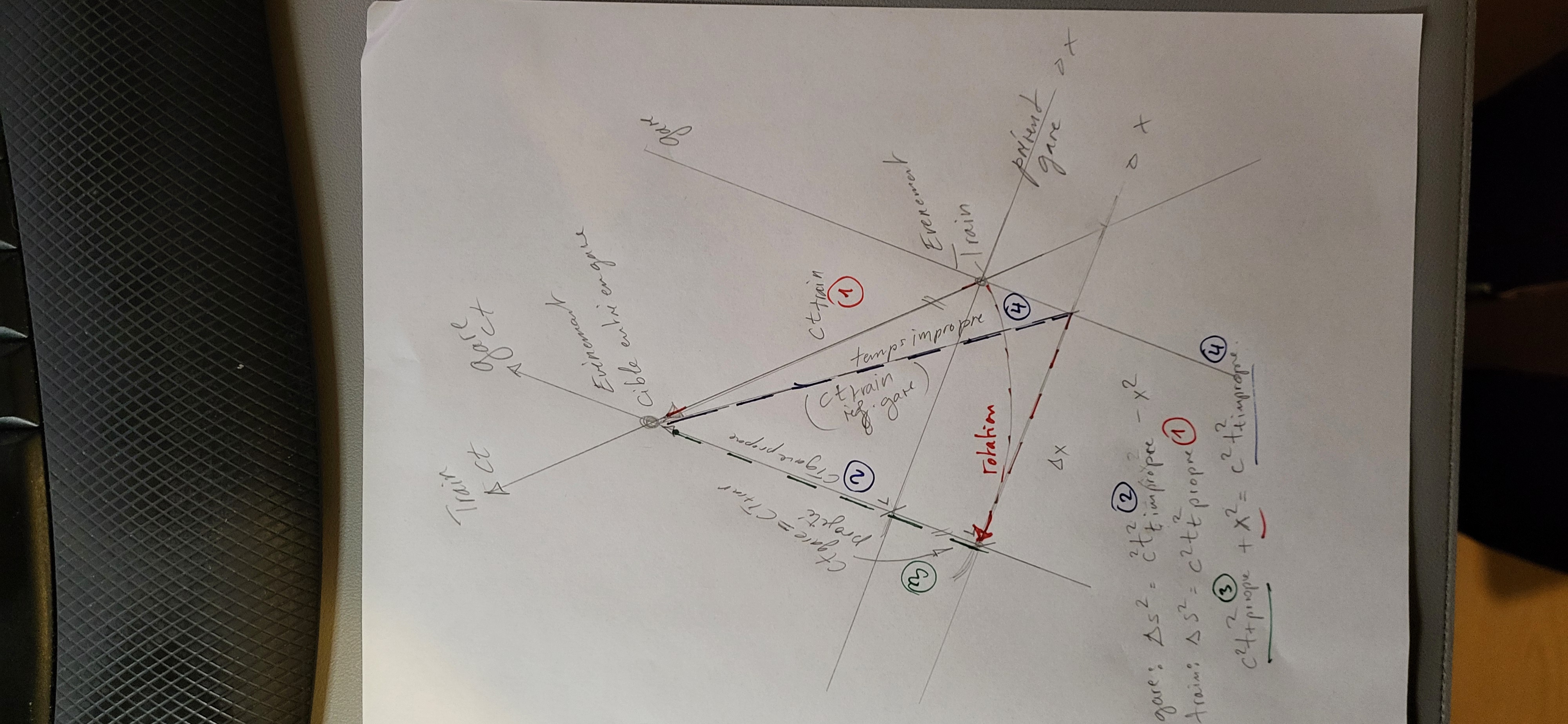
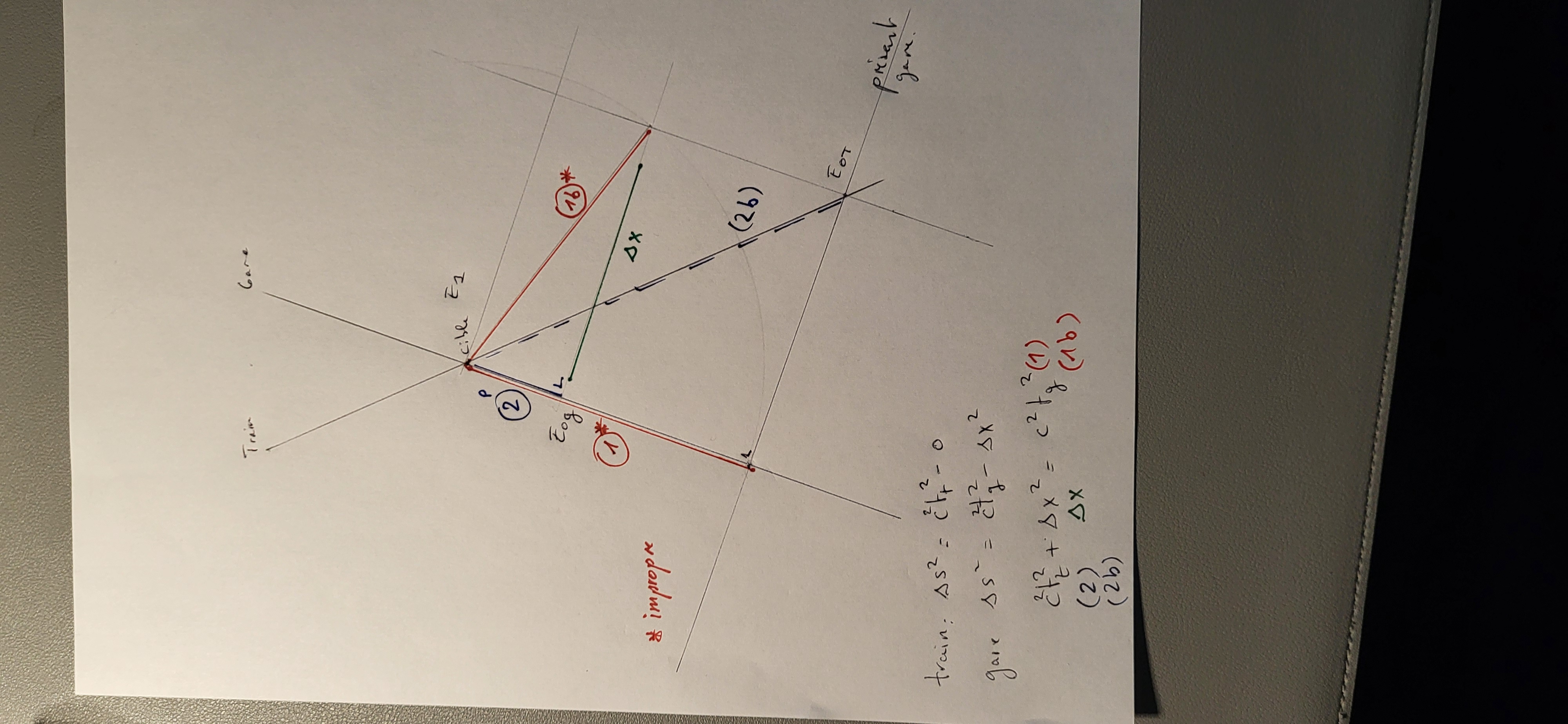
On prend le cas le plus simple possible d'un train qui entre en gare
On sait que l'intervalle espace temps au carré est conservé : s2 = c2* t2 -x2
On a 1 événement cible "entrée en gare"
On a 2 événements (train départ et gare départ) qui ont une distance identique c*tg (temps propre gare) = c*tt (temps propre train) par rapport à l'événement entrée en gare : ?
Et x la distance entre la gare et le train dans le référentiel de la gare pour l'événement train départ.

Si on projette le temps propre du train (train->entrée gare) sur l'axe des événements gare -> entrée en gare. On a sur l'axe de la gare, la distance temps propre du train.
Si on applique Pythagore avec le temps propre du train (qui est aussi quelque part celui de la gare à un autre moment de départ ?) dans le référentiel de la gare, on trouve c2 * t(propre-projete)2 + x2 = c2 (le temps IMpropre du train dans le référentiel de la gare) 2
Donc si on observe "son" temps propre en mouvement aussi dans l'espace et pas uniquement dans le temps, alors le temps observé ou IMpropre est plus grand. Ce qui semble très "normal".
-----

[mach3]

Est-il possible d’avoir une description plus claire et plus précise ? En l’état je ne parviens pas à comprendre la situation.

(Par ailleurs un petit bonjour et merci ne seraient pas de trop)

m@ch3

[jlthirot]

Bonsoir,

Merci pour avoir pris le temps de lire mon message.20241206_004825.jpg

[jlthirot]

Avec une autre image

[A voir en vidéo sur Futura]

[lafysikCmoi]

je lis plusieurs temps, tpropre, timpropre, tgare, tgarepropre, ttrain, ttrainrefgare, t. Sur quelles horloges sont lues ces horaires?

[jlthirot]

je lis plusieurs temps, tpropre, timpropre, tgare, tgarepropre, ttrain, ttrainrefgare, t. Sur quelles horloges sont lues ces horaires?

Bonjour,
J'ai interprété ainsi:
tpropre = est le temps mesuré dans le référentiel qui n'est pas en mouvement dans l'espace par rapport aux événements
timpropre = le temps mesuré d'un phénomène en mouvement dans l'espace par rapport au référentiel de mesure

Je pourrais ajouter une information pour préciser l'horloge de ref. Mais ici toutes les mesures sont faites depuis le référentiel gare sauf pour le temps propre No 1 entre le départ du train et son arrivée, le temps propre du train. Son temps impropre est le No 4, donc le temps mesuré dans le ref Gare.

[lafysikCmoi]

et les autres?

[jlthirot]

et les autres?

Le No 2 est un temps impropre des évènements train, car mesuré dans le ref gare
Le No 3 est le temps propre des événements gare-entrée gare mesurés dans le ref gare. Ce temps est choisi comme étant égale au temps propre du train-entre en gare.

L'idée est que la cible entrée du train en gare est entourée de distances temps ct propres identiques pour la direction train ou gare.
Est-ce que cette supposition est légitime et est-ce que la rotation est légitime ?

[jlthirot]

Correction Le No 3 est le temps propre des événements gare-entrée gare
Je pense que le No 3 n'est PAS mesurable.

[Amanuensis]

Base fondamentale : une durée propre est la durée mesurée par une horloge entre deux événements la concernant. La valeur dépend du chemin suivie par l'horloge entre ces événements.

La seule différence avec la mécanique usuelle est la dépendance au chemin: en classique, la durée mesurée ne dépend que des événements, pas du chemin suivie par l'horloge.

Le temps propre d'une horloge est ce qu'elle indique.

C'est aussi simple que ça, et tant qu'on a pas parfaitement "absorber" cette idée, pas de salut.

Toute mention de "temps propre" autrement que le long d'un chemin rend le texte sans sens, et ne mérite pas de réponse.

(Et une durée "impropre" est une différence de coordonnées temporelles.)

[jlthirot]

l'operation de rotation ne me semble pas juste. Une grande vitesse ou angle devant amener à des temps impropres qui peuvent tendre vers l'infini.

Est-ce vraiment illégitime de basculer le temps propre du train vers la gare ?
Pourquoi, on ne peut pas le faire ?
Est-ce que l'entrée en gare de la gare est si différent de l'entrée en gare du train, modulo l'espace x ?

[Amanuensis]

Est-ce vraiment illégitime de basculer le temps propre du train vers la gare ?

Qu'entendez-vous par "basculer" ? Une horloge immobile relativement au train indique le temps propre du chemin qu'elle suit, une autre horloge, immobile relativement à la gare indique le temps propre du chemin qu'elle suit.

Pourquoi, on ne peut pas le faire ?

Faire quoi? On peut prendre des photos successives montrant ce que les horloges indiquent à différents "moments" (différents événements).

Est-ce que l'entrée en gare de la gare est si différent de l'entrée en gare du train, modulo l'espace x ?

Pas clair, à ré-exprimer? L'entrée du train dans la gare est un événement unique, indépendamment de qui le regarde ou le photographie.

[jlthirot]

Schéma moins faux

Le temps propre étant toujours plus petit que le temps impropre.

[jlthirot]

Qu'entendez-vous par "basculer" ?

C'est passer de 2b à 2

Faire quoi?

Peut-être que les natures du temps et de l'espace out toute autre raison empêche de faire cette opération qui n'aurait aucun sens physique

Pas clair, à ré-exprimer? L'entrée du train dans la gare est un événement unique, indépendamment de qui le regarde ou le photographie.

Une gare qui rentre en gare est, la gare au temps x puis la gare au temps x+deltax. Dans le dernier schéma ce sont les événements Eog et E1.

[jlthirot]

Je vu qu'il existe des abaques en papier pour manipuler la RR. On peut aussi poser ce cas dans le Diagramme de Minkowski.
Mais n'étant plus à l'école, j'ai le droit de faire toutes les erreurs nécessaires.

[jlthirot]

Une gare qui rentre en gare est, la gare au temps x puis la gare au temps x+deltax. Dans le dernier schéma ce sont les événements Eog et E1.

Evidemment c'est t et non x !!

[Amanuensis]

Je vu qu'il existe des abaques en papier pour manipuler la RR. On peut aussi poser ce cas dans le Diagramme de Minkowski.

Note de détail (mais qui a son importance) : ce n'est pas "manipuler la RR", mais manipuler l'espace-temps de Minkowski.

Ce n'est pas avec ces abaques en papier que vous pourrez maîtriser le sujet de la RR, comme par exemple les calculs sur les accélérations (e.g., coordonnées de Rindler).

[ordage]

Bonjour
Dans les ouvrages modernes sur la relativité, le chapitre "relativité restreinte" (RR) ne s'intéresse pas du tout à la simultanéité. Ils décrivent l'espace-temps de la RR avec ses propriétés "géométriques".

Au début de la RR, ce problème qui stigmatisait les différences entre la mécanique classique et la relativité a été souvent développé (Par Einstein entre autres).

Pédagogiquement c'était sans doute louable, parce que, en définissant un "référentiel balisé et synchronisé" on se raccrochait aux concepts classiques de temps et d'espace newtoniens, qu'on connaissait bien et comme , avec ces concepts, cela ne marchait pas entre différents référentiels, cela illustrait bien la différence des théories. Mais à part cela, la simultanéité en RR n'a pas d'intérêt physique (voir post Amenuensis).

Dans l'interprétation, quand on lit des vocables comme "temps propre", "longueur propre" il faut bien comprendre à quoi cela correspond. Ce sont des "intervalles d'espace-temps", de type temps, pour le temps propre (caractérisés par le signe "moins" du ds² dans la convention (-,+,+,+), ou s² quand c'est intégré et de type espace (signe + du ds² et s²) pour la longueur propre. Etant des intervalles d'espace temps le s² qui mesure cet espace-temps est invariant, dans tous les référentiels et système de coordonnées.

Quant au temps impropre, espace impropre (vocables non normalisés) je suppose qu'ils se réfèrent à des coordonnées, qui sont arbitraires et non invariantes. Comme guide de lecture, il faut bien garder à l'esprit ces fondamentaux pour interpréter correctement une situation et déterminer ce qui est physique et ce qui ne l'est pas.
Par exemple quand on mesure sur le ballast la longueur d'un train à vitesse constante, ce qui est physique c'est le train (longueur propre mesurée dans le train dont le s² vaut par exemple s0² dont la composante temporelle est nulle (le train est supposé balisé et synchronisé) , ce qu'on mesure sur le talus (balisé et synchronisé), c'est une mesure qui correspond à la composante spatiale l de ce s0² dont la composante temporelle t n'est pas nulle ce qui fait que le s²= -t²+x² = s0². On constate l'invariance de l'intervalle d'espace-temps de longueur du train.

Cordialement

[f6bes]

Je visualise mal " ..une gare qui entre gare .." ? Cela ecrit par deux fois.
Les ttrains n'ont qu'à bien se tenir...c'est les gares qui se déplacent !!
A+

[Amanuensis]

Même en relativité galiléenne, les gares se déplacent. La surface de la Terre aussi. La Terre aussi. Le Système solaire aussi...

[jlthirot]

J'ai des réponses
Oui on peut représenter ces distance sous la forme d'un triangle rectangle
Extraits de la page wiki https://fr.wikipedia.org/wiki/Ligne_d%27univers, chapitre "Illustration simple

Oui ce type de diagramme existe il a pour nom "diagramme de Loedel"
https://owl-ge.ch/IMG/pdf/Relativite...pace-temps.pdf

L'interprétation que le phénomène des événements train > entrée en gare à son équivalent gare > entrée en gare me semble valide. (C'est probablement une évidence)

[Amanuensis]

L'interprétation que le phénomène des événements train > entrée en gare à son équivalent gare > entrée en gare me semble valide. (C'est probablement une évidence)

Ne serait-ce pas plutôt gare > entrée en train ?

À part ça, oui, d'une certaine manière c'est une évidence, ou plus exactement une application triviale de la "loi" disant qu'un mouvement est toujours relatif.

[jlthirot]

Ne serait-ce pas plutôt gare > entrée en train ?

À part ça, oui, d'une certaine manière c'est une évidence, ou plus exactement une application triviale de la "loi" disant qu'un mouvement est toujours relatif.

Non c'est bien gare > entrée en gare et si je voulais être précis et plus exhaustif, plutôt que de faire un jeu de mot, c'est.

L'idée était de se placer à la place de la Gare (Future) et d'observer depuis cet endroit la gare* et le train* qui arrivent.
*est un rappel que la Gare et la gare* ne sont pas le même événement et que la gare* est probablement une succession d'événements gare

Gare (Future) < arrivée de la gare* et Gare (Future) < arrivée du train*
et respectivement pour le train
Train (Future) < arrivée du train* et Train (Future) < arrivée de la gare*