Bonjour
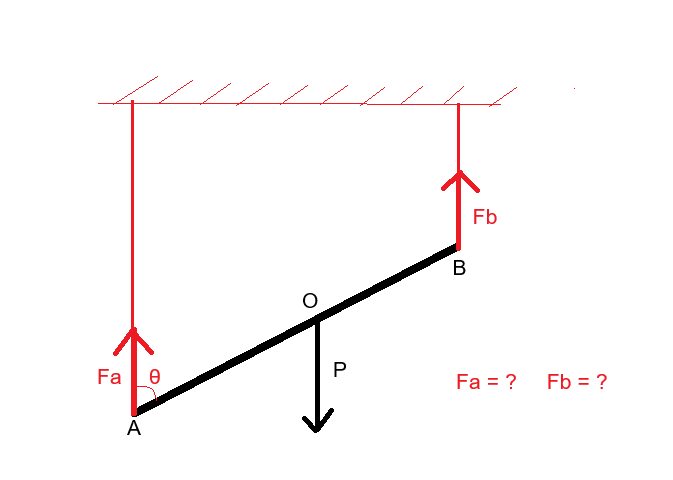
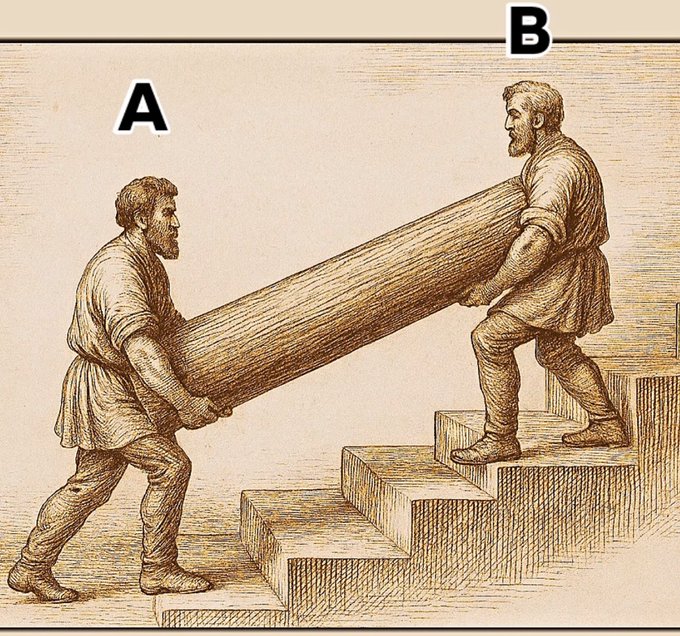
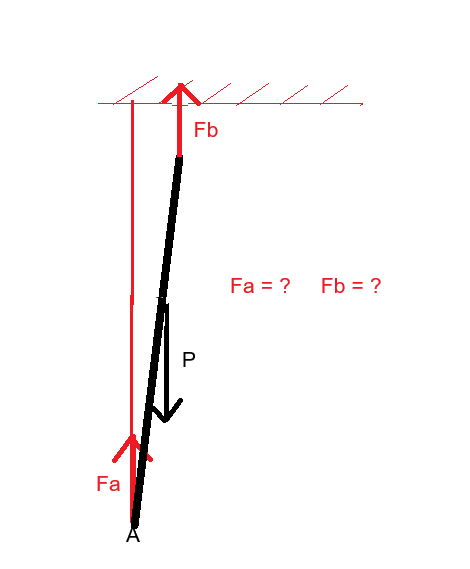
Soit une barre de poids P maintenue par 2 fils aux points A et B comme indiqué sur le schéma joint.
Comment déterminer les forces Fa et Fb appliquées aux points A et B ?
La barre est en équilibre, donc Fa + Fb + P = 0 (vecteurs)
Les moments de Fa et Fb par rapport à 0 sont également nuls. OA ^Fa + OB ^Fb = 0 (vecteurs)
Si les 2 fils sont verticaux alors on montre facilement que Fa = Fb = P / 2
Mais sont-ils verticaux ?
Plus on incline la barre en diminuant θ, plus on a le sentiment que Fa > Fb
Qu'en pensez-vous svp ?
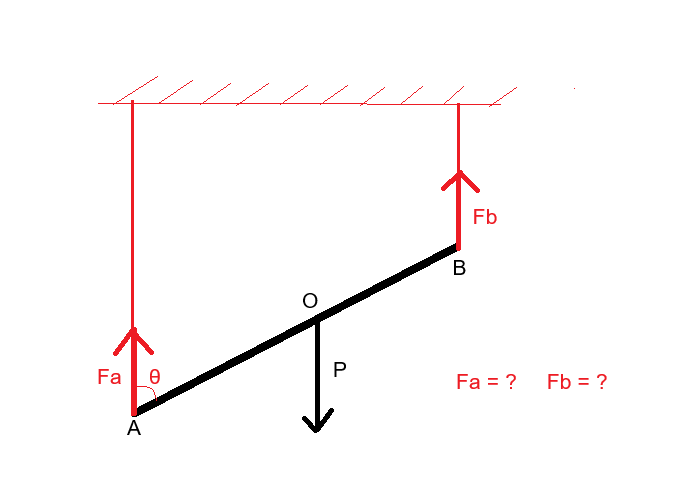
-----



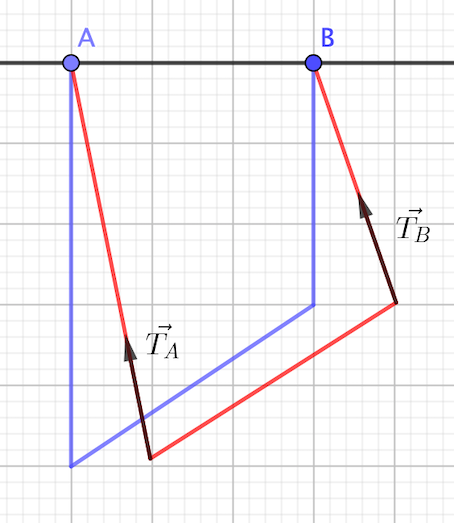


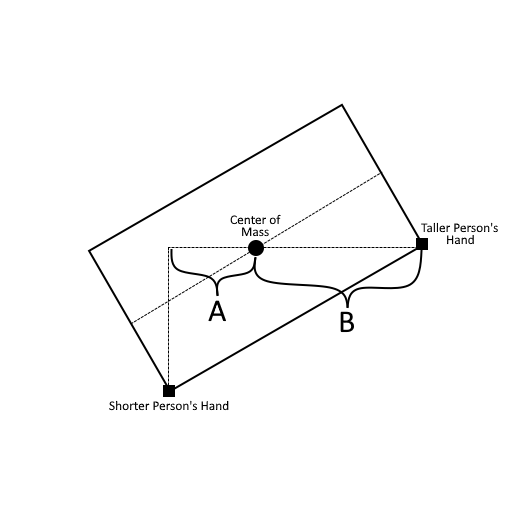
 avec L longueur de la barre, lA et lB longueurs des fils et d distance entre les points d'accroche.
avec L longueur de la barre, lA et lB longueurs des fils et d distance entre les points d'accroche.