Paradoxe des jumeaux

[bobdémaths]

Re,

J'aimerais montrer que la méthode que j'ai décrite ci-dessus, qui se base uniquement sur les quelques principes résumés dans ce que j'ai cité d'Amanuensis, permet de résoudre facilement tous ces problèmes.

Attaquons-nous donc à celui-ci :

Soit cinq balises fixes B1 B2 B3 B4 B5 les une par rapport aux autres et deux jumeaux J1 J2.
Les jumeaux accélèrent uniformément de B1 en même temps et arrivent avec la même vitesse Vmax au niveau de B2 en même temps.

En arrivant à B2, J1 cesse d'accélérer et se dirige à vitesse constante Vmax vers B3 ; J2 freine avec la même amplitude que durant la phase d'accélération et arrive en B3 avec une vitesse nulle.

J2 accélère en direction de B2 qu'il atteint avec une vitesse = Vmax.
J2 décellère en direction de B1 qu'il atteint avec une vitesse nulle.

J1 atteint B4 avec une vitesse = Vmax et commence à décéllerer vers B5.
J1 atteint B5 avec une vitesse nulle.

J1 repart vers B4 qu'il atteint avec une vitesse = Vmax.
J1 atteint B2 avec une vitesse = Vmax et décellère vers B1
J1 atteint B1 avec une vitesse nulle.

Vu que les accélérétations sont identiques entre B1-B2 ; B2-B3 ; B4-B5 je pense que dans le référentiel inertiel des balises, les distance entre les balises précitées sont égales.

chacun des deux jumeaux ayant connu les même phase d'accélérétion et decélération. si J1 revient plus jeune que J2, pourquoi le référentiel de J1 garde t'il "en mémoire" que c'est lui qui reviendra plus jeune que J2 et non l'inverse pendant le temps où il évoluera à V=Vmax par rapport aux balises?

Le problème semble compliqué au premier abord. Et pourtant, voyons ce que nous dit la méthode :

- Il existe une classe de référentiels privilégiés, appelés référentiels inertiels. Dans un de ces référentiels, comme l'a dit Amanuensis, le chemin le plus long entre deux événements de même position spatiale est l'immobilité dans ce référentiel. Tous les autres chemins sont plus courts (c'est l'inverse de la géométrie euclidienne, où la ligne droite est le plus court chemin, ici c'est le plus long, à cause du signe - dans la métrique).
- Deuxième ingrédient : la "longueur" d'un chemin correspond au vieillissement (c'est le temps propre, intégré sur le chemin).
- Troisième ingrédient : le référentiel de la Terre est un référentiel inertiel.
- Conclusion : dans le référentiel de la Terre, pour aller d'un événement A à un événement B qui ont la même position spatiale, un voyageur qui reste immobile vieillit plus tout autre voyageur qui bouge.

Pour enfoncer le clou, on peut prendre une analogie dans l'espace euclidien (donc avec une signature + + +, et sans le temps). Il faut faire les substitutions suivantes :
Le vieillissement -> la distance parcourue pendant le voyage.
Rester immobile -> voyager en ligne droite.
Alors le paradoxe des jumeaux devient le suivant.
Le jumeau A voyage de la Terre vers la Lune en ligne droite. Le jumeau B voyage de la Terre vers la Lune en faisant une escale sur Mars. J'affirme alors : la distance parcourue par le jumeau A est inférieure à celle parcourue par le jumeau B.
Cela te semble-t-il paradoxal ? Bien sûr que non.
Bien sûr, on peut faire un changement de coordonnées tel que le jumeau B voyage en ligne droite dans ce système de coordonnées. Mais on ne peut évidemment pas appliquer le raisonnement dans ce nouveau référentiel, car la métrique n'est plus euclidienne !


Comme vous le voyez:
1) Il est complètement inutile de préciser la nature du mouvement du jumeau voyageur. Le simple fait qu'il soit en mouvement suffit.
2) En particulier, toutes les histoires d'accélération, de demi-tour, et autres fioritures, ne servent qu'à illustrer, mais ne sont absolument pas nécessaires.
3) Le problème est purement géométrique (dans un espace doté d'une métrique bien précise). Ce n'est donc pas un problème de physique, et faire intervenir la gravitation est hors de propos.

Après ces rappels, appliquons la méthode.
- Un référentiel inertiel est le référentiel géocentrique (que j'appelle "de la Terre"). On appelle x et t les coordonnées d'espace et de temps dans ce référentiel, et pour simplifier on ne prend qu'une dimension d'espace.
- On dessine un diagramme avec x en abscisse et t en ordonnée. Puis on trace les trajectoires des deux jumeaux.
- Le vieillissement correspond à la "longueur de la trajectoire dans l'espace-temps", et cette longueur est d'autant plus courte que la longueur de la trajectoire dessinée sur le diagramme est longue.
- Conclusion : Le jumeau qui a la trajectoire sur le diagramme la plus longue sera le plus jeune à l'arrivée.

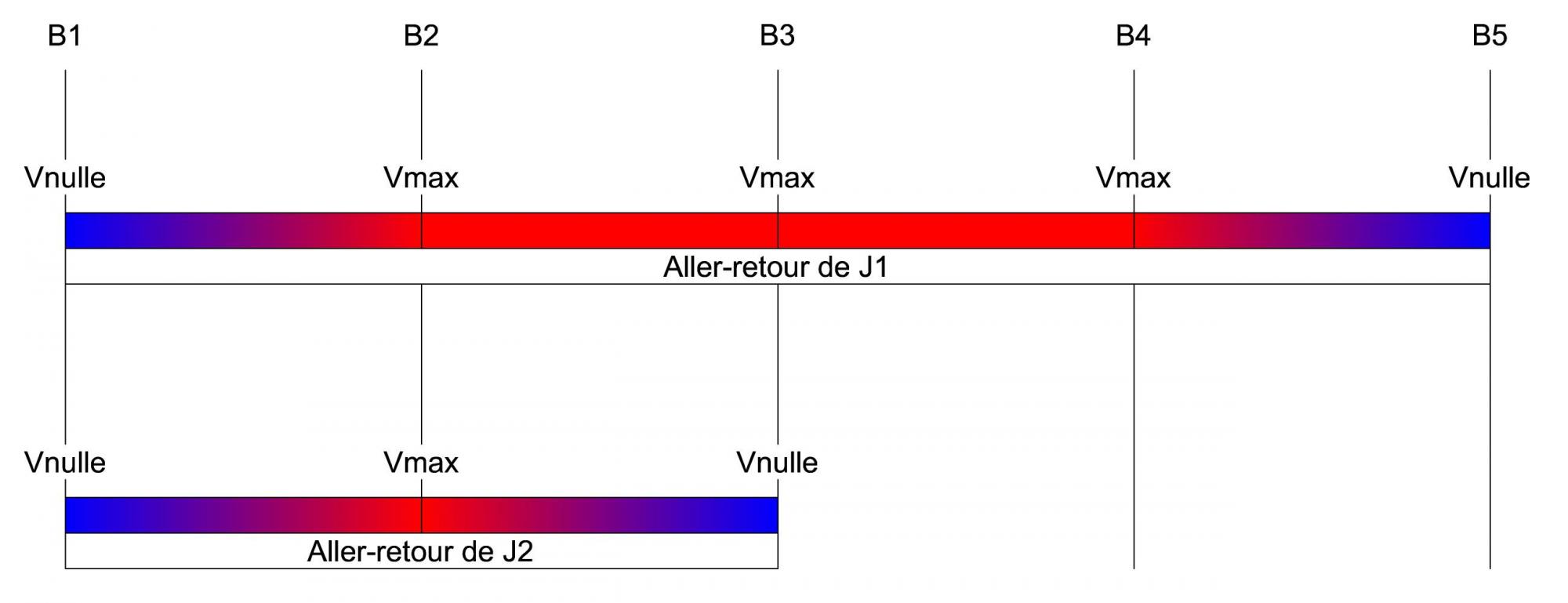
Remarques : on se fiche éperdument des détails de la trajectoire, il suffit de regarder laquelle est la plus longue. Dans ton exemple précis, la trajectoire sera formée de morceaux de droites et de morceaux de paraboles (les phases d'accélération), donc il n'est pas tout à fait trivial de calculer la longueur, mais ça se fait (et ça se voit à l’œil pour comparer). Si tu négliges les phases d'accélération, tu n'auras que des morceaux de droites, et la distance est plus facile à évaluer.

Donc maintenant tu as la méthode pour résoudre tous les cas possibles de jumeaux avec des trajectoires quelconques !
-----

[Amanuensis]

- Le vieillissement correspond à la "longueur de la trajectoire dans l'espace-temps", et cette longueur est d'autant plus courte que la longueur de la trajectoire dessinée sur le diagramme est longue.

Malheureusement, non. La métrique étant dt²-dx², on ne peut pas mesurer les durées propres sur la feuille (on mesure dt²+dx²).

On est en pratique obligé de passer par les calculs analytiques. Ceci dit, la figure est un moyen pour bien présenter les trajectoires...

[rik 2]

bon! une dernière fois!Soit deux référentiels R et R', munis des distances d, d' et des mesures de temps n, n' respectivement, en mru l'un par rapport à l'autre.

1. Invariance des mesures propres.
1a. Invariance des longueurs propres: d'(A', B') = d'(f(A), f(B)) = d(A, B) = L°
1b. Invariance des temps propres: n'(t'°) = n'(g(t°)) = n(t°) = t°

2. Variation des mesures propres d'un des référentiels.
2a. Contraction des longueurs propres: d'(A', B') = L' = k d(A,B) = k L°
2b. Dilatation des temps propres: n'(t'°) = n(t°)/k = t°/k

3. Variation des mesures apparentes.
3a. Contraction des longueurs apparentes: d(A', B') = L = k d'(A', B') = d'(A,B) = L' = k L°
3b. Dilatation des temps apparents: n(t') = n'(t'°)/k = n'(t) = n(t°)/k = t°/k

La proposition 2a est l'hypothèse de Lorentz. Amha, 2a et 2b sont indissociables.

1 et 3 sont compatibles; mais ces deux ne résultent-ils pas de la relativité einsteinienne?

[Mailou75]

Soit cinq balises fixes B1 B2 B3 B4 B5 les une par rapport aux autres et deux jumeaux J1 J2.
Les jumeaux accélèrent uniformément de B1 en même temps et arrivent avec la même vitesse Vmax au niveau de B2 en même temps.
En arrivant à B2, J1 cesse d'accélérer et se dirige à vitesse constante Vmax vers B3 ; J2 freine avec la même amplitude que durant la phase d'accélération et arrive en B3 avec une vitesse nulle.
J2 accélère en direction de B2 qu'il atteint avec une vitesse = Vmax.
J2 décellère en direction de B1 qu'il atteint avec une vitesse nulle.
J1 atteint B4 avec une vitesse = Vmax et commence à décéllerer vers B5.
J1 atteint B5 avec une vitesse nulle.
J1 repart vers B4 qu'il atteint avec une vitesse = Vmax.
J1 atteint B2 avec une vitesse = Vmax et décellère vers B1
J1 atteint B1 avec une vitesse nulle.

Une illustration possible pour ton problème (somme de portions de droites)
J2 en rouge, J1 en violet et un observateur fixe en B1 bleu

[Mailou75]

Oups.. j'me suis trompé en comptant

(merci aux modos d'éffacer le dessin précédent il est faux, celui ci le remplace, merci )

[bobdémaths]

Malheureusement, non. La métrique étant dt²-dx², on ne peut pas mesurer les durées propres sur la feuille (on mesure dt²+dx²).

On est en pratique obligé de passer par les calculs analytiques. Ceci dit, la figure est un moyen pour bien présenter les trajectoires...

En effet je me suis surement un peu emballé. Voyons exactement où. On se place dans le référentiel de la Terre, coordonnées x et t. Prenons deux jumeaux, avec des trajectoires paramétrées par t variant entre 0 et T : et . On suppose (les deux événements de départ et d'arrivée sont à la même coordonnée spatiale, prise à 0).
Je pose et . Les longueurs des trajectoires mesurées sur le diagramme sont
et .
Les longueurs dans l'espace-temps (temps propre intégré) sont
et .

Ce que j'ai affirmé, c'est l'implication suivante :

.

Je ne vois pas pourquoi elle serait vraie, même si je n'ai pas de contre-exemple sous la main.

Cependant est clairement vraie dans les cas particuliers suivants :
1) Y=0 (paradoxe des jumeaux classique, ce que j'expliquais dans le message #17)
2) sur toute la trajectoire (l'un des jumeaux va toujours plus vite que l'autre, à tout instant ; c'est le cas dans l'histoire qui nous occupait dans mon message #31)

Il serait intéressant de déterminer des conditions nécessaires et suffisantes (ou simplement suffisantes) pour que l'implication soit vraie. En faisant le développement des racines, j'obtiens une condition sur les "moments" de X et Y, mais ce n'est pas très élégant. Je vais voir si je trouve mieux. Peut-être est-il plus efficace de commencer par trouver plusieurs contre-exemples.

[astrocurieux]

Le problème du référentiel inertiel est central ici.
Tu seras d'accord bob qu'avant de faire des calculs il faut choisir nos repères, et là nous avons un problème.

Qu'est-ce qu'un référentiel inertiel ?

Que dit wiki : http://fr.wikipedia.org/wiki/R%C3%A9...ntiel_inertiel

j2 peut-il être un référentiel inertiel ?
Deux choses agissent sur j2 : le milieu dans lequel il se trouve et son mouvement par rapport à ce milieu.
j2 ne sera plus un référentiel inertiel si l'un de ces facteurs change au fil du temps, c'est-à-dire si la densité d'énergie du milieu évolue ou s'il accélère (à moins peut-être que les deux se compensent).
j2 sera un référentiel inertiel s'il a un mouvement rectiligne uniforme dans un milieu homogène et constant.

[astrocurieux]

j2 sera un référentiel inertiel s'il a un mouvement rectiligne uniforme dans un milieu homogène et constant.

Mais même comme cela, ça ne marche pas, il n'y a pas réciprocité, on ne peut pas considérer j2 comme fixe et j1 en mouvement, cela ne marcherait pas.

[Amanuensis]

Il serait intéressant de déterminer des conditions nécessaires et suffisantes (ou simplement suffisantes) pour que l'implication soit vraie.

Si on prend seulement l'ordre, alors c'est bon pour les trajectoires temporelles. Quand je disais qu'on ne pouvais pas mesurer, je parlais de la valeur précise. Mais maintenant je réalise que votre assertion portait juste sur l'ordre, désolé.

Si on prend un segment de longueur 1 sur la feuille, il a pour coordonnées (cos alpha, sin alpha), et la "durée" est cos² alpha -sin² alpha = cos 2alpha [pour temps en abscisse et espace en ordonnée]. La fonction est décroissante (ce qu'on veut) sur ]0, pi/2[, qui est l'intervalle qui nous intéresse (vitesses de genre temps, les directions d'angle +/- pi/2 étant les directions nulles).

L'ordre est bien conservé, et l'erreur de mesure est d'autant plus grande qu'on s'approche des diagonales (normal, la durée propre tend vers 0, ce qui n'est pas le cas sur la feuille...).

[Amanuensis]

Après réflexion, mon message précédent ne paraît pas pertinent, et même erroné dans sa conclusion... Réflexion supplémentaire nécessaire!

[invite6754323456711]

Oups.. j'me suis trompé en comptant

Une représentation avec trois arcs d'hyperbole pour le voyageur.

Patrick

[PPathfindeRR]

à Zefram Cochrane

Si j'ai bien compris ton expérience :

Même accélération et décélération (en violet), et même vitesse (en rouge).



Alors pour moi, J1 et J2 gardent le même age une fois réunis...
En bleu et en rouge pour un repère inertiel et en violet pour un repère non inertiel.
Par exemple, quand J1 accélère ou décélère, son horloge tourne plus lentement, et quand il atteint une vitesse constante ou qu'il est au repos, son horloge tourne plus vite.

Le principe dont Amanuensis et bobdémaths ne partage pas; qui selon eux, si j'ai bien compris leurs explications (que je n'arrive toujours pas à me représenter), que dans deux référentiels inertiels le temps peut s'écouler différemment.

pour moi, un référentiel dit inertiel, est un référentiel dont une personne ou un objet de subit pas de force extérieure (comme l'impesanteur, une vitesse constante, etc...);
Et non inertiel comme lorsque qu'on subit une accélération ou décélération (un changement de vitesse), ou encore la Terre dont on subit la force de gravité.

en faite je me pose des questions sur l’énergie qui fait tourner l'horloge (l'énergie du ressort) et l'énergie nécessaire pour changer la vitesse constante de celle-ci, soit une accélération et les forces d'inertie qui s'exercent sur l'horloge... je me demande s'il n'y aurai pas un transfère d'énergie qui cause le ralentissement de l'horloge, à aiguille ou atomique.. ou même les atomes qui compose le jumeaux et son vieillissement lors d'une accélération ou décélération.

En tous cas, j'ai du mal à voir claire dans tous ceci !

[Amanuensis]

Le principe dont Amanuensis et bobdémaths ne partage pas; qui selon eux

Ce n'est pas "selon nous", ce n'est pas matière à opinion. Ce qui est fait dans ce fil comme dans bien d'autres, ce sont des maths, l'examen du modèle bien précis et parfaitement défini qu'est l'espace-temps de Minkowski.

Merci de ne pas faire penser que ceux qui se contentent d'exposer les maths telles qu'elles sont (plutôt que faire du bla-bla littéraire développant une vague philosophie de l'espace et du temps) débattraient de quoi que ce soit.

Soit les maths, formule, calculs, sont corrects, soit ils ne le sont pas. Ce n'est pas une questions d'opinion.

[Exemple: non, J1 et J2 n'ont pas le même âge aux retrouvailles. Ce sont les maths qui le disent, ce n'est pas un sujet à débat.]

pour moi, un référentiel dit inertiel, est un référentiel dont une personne ou un objet de subit pas de force extérieure (comme l'impesanteur, une vitesse constante, etc...);
Et non inertiel comme lorsque qu'on subit une accélération ou décélération (un changement de vitesse), ou encore la Terre dont on subit la force de gravité.

Vous sortez du cadre de la RR.

[PPathfindeRR]

à Amanuensis,

Ne le prend pas mal, je me suis mal exprimé.
je ne parlais pas de VOTRE opinion, votre compréhension de la relativité est surement meilleure que la mienne.

Non, ce que j'ai du mal comprendre, c'est que ce ne soit pas l'accélération ou autre forme causant la pesanteur qui est responsable du ralentissement de l'écoulement du temps comme je croyais comprendre (ce transfert d'énergie que je cite plus haut)... mais que le temps peut s'écouler différemment dans deux référentiels inertiels comme vous me le faite savoir.

et justement, en RR on ne parle que de référentiels inertiels, s'il y a accélération, gravité, pesanteur... on ne parle plus de référentiel inertiel donc c'est le cadre de la RG ?

[invite6754323456711]

Merci de ne pas faire penser que ceux qui se contentent d'exposer les maths telles qu'elles sont (plutôt que faire du bla-bla littéraire développant une vague philosophie de l'espace et du temps) débattraient de quoi que ce soit.

Soit les maths, formule, calculs, sont corrects, soit ils ne le sont pas. Ce n'est pas une questions d'opinion.

C'est l'ubuesque de la situation, bien souvent répété sur FS ou on cherche d'abord à se construire une opinion fortement corrélé avec nos perceptions immédiates de environnement avant même de lire et chercher à comprendre le cadre mathématique tel que le tenseur métrique pour ensuite mieux comprendre l'interprétation physique du tenseur métrique, opérateur donnant le temps le long la trajectoire d'un point matériel à savoir la ligne d'univers.

Patrick

[Zefram Cochrane]

à Zefram Cochrane

Si j'ai bien compris ton expérience :

Même accélération et décélération (en violet), et même vitesse (en rouge).

Pièce jointe 219358

Alors pour moi, J1 et J2 gardent le même age une fois réunis...
En bleu et en rouge pour un repère inertiel et en violet pour un repère non inertiel.
Par exemple, quand J1 accélère ou décélère, son horloge tourne plus lentement, et quand il atteint une vitesse constante ou qu'il est au repos, son horloge tourne plus vite.

Le principe dont Amanuensis et bobdémaths ne partage pas; qui selon eux, si j'ai bien compris leurs explications (que je n'arrive toujours pas à me représenter), que dans deux référentiels inertiels le temps peut s'écouler différemment.

pour moi, un référentiel dit inertiel, est un référentiel dont une personne ou un objet de subit pas de force extérieure (comme l'impesanteur, une vitesse constante, etc...);
Et non inertiel comme lorsque qu'on subit une accélération ou décélération (un changement de vitesse), ou encore la Terre dont on subit la force de gravité.

en faite je me pose des questions sur l’énergie qui fait tourner l'horloge (l'énergie du ressort) et l'énergie nécessaire pour changer la vitesse constante de celle-ci, soit une accélération et les forces d'inertie qui s'exercent sur l'horloge... je me demande s'il n'y aurai pas un transfère d'énergie qui cause le ralentissement de l'horloge, à aiguille ou atomique.. ou même les atomes qui compose le jumeaux et son vieillissement lors d'une accélération ou décélération.

En tous cas, j'ai du mal à voir claire dans tous ceci !

Bonsoir,

Pour moi et ce que montre aussi le schéma de Mailou que je remercie au passage, c'est que pour appliquer la méthode que propose Boblesmath et Amanuensis, il faut en préalable définir quel est le référentiel inertiel stationnaire ici les balises ce qui est une démarche très relativiste je trouve , pour savoir lequeldes jumeaux J1 et J2 vieilliera plus que l'autre. Je serai curieux de voir ce que donnerai le schéma en considérant J1 fixe dans son référentiel et ensuite J2.
Si tu soustrait sur le schéma de Mailou la surface correspondant à la courbe de J2 à celle de J1 tu obtiendra un rectangle.qui correspond au portions de la trajectoire dont la vitesse realtive entre J1 et J2 est constante. ce que l'on voit aussi également sur ton schéma.

Pour moi, d'après le principe d'équivalence, la vitesse de la lumière dans les référentiels de J1 et J2 a diminué lors de la phase d'accélérération, et cette diminution est fonction de ce qu'on appelle en RG la vitesse de libération.

Pour J2 c'est facile : au fur et à mesure qu'il accélère la vitesse de la lumière diminue, après avoir atteint une vitesse max, il décélère, la vitesse de la lumière augmente. il accélère de nouveau, la vitesse de la lumière baisse, il décélère, la vitesse de la lumière augmente.
C'est comme s'il sautait d'une plateforme en B1 sur un trempoline en B2 puis rebondissait sur une plateforme en B3 situé à la même hauteur que B1 puis ressautait sur le trempoline en B2 pour revenir à B1.

Pour J1 on imagine mal la vitesse de la lumière diminuer pour atteindre une valeur min en B2, puis revenir à la valeur max (celle du référentiel des balises) parce que la vitesse de la lumire est une constante, revenir instantanément à sa valeur min en B4 parce qu'elle doit de nouveau augmenter pour atteindre sa valeur max en B5.

La vitesse de la lumière est le paramètre variable qui détermine pour lequel des jumeaux J1 et J2 le temps propre s'écoule le moins rapidement lors de leur voyage.

Cordialement,
Zefram

[Amanuensis]

Je serai curieux de voir ce que donnerai le schéma en considérant J1 fixe dans son référentiel et ensuite J2.

Pour une n-ième fois, il n'y a pas en RR de référentiel canonique dans laquelle une trajectoire accélérée serait immobile (c'est le cas en mécanique classique pour un solide indéformable, mais PAS en RR). On ne peut donc pas parler de "son" référentiel ; si on veut vraiment (ce n'est pas une bonne idée en général) travailler avec un référentiel (partiel) relativement auquel J1 est fixe, il faut le décrire.

---

Le reste est nawak

[PPathfindeRR]

oups, pardon tout le monde !
ça à répondu tellement vite que j'ai carrément zappé la page 3 !
Bon je lire tout ça.

[Zefram Cochrane]

Pour une n-ième fois, il n'y a pas en RR de référentiel canonique dans laquelle une trajectoire accélérée serait immobile (c'est le cas en mécanique classique pour un solide indéformable, mais PAS en RR). On ne peut donc pas parler de "son" référentiel ; si on veut vraiment (ce n'est pas une bonne idée en général) travailler avec un référentiel (partiel) relativement auquel J1 est fixe, il faut le décrire.

Ca doit pouvoir se faire.

Le reste est nawak

Nous n'avons pas la même compréhension du principe d'équivalence.

Cordialement,
Zefram

[Amanuensis]

Nous n'avons pas la même compréhension du principe d'équivalence.

Disons que la compréhension de l'un ne peut pas se comparer avec l'incompréhension de l'autre.

[Zefram Cochrane]

Tout à fait parfois on a tendance à mal interpréter ce que Relativité générale veut dire.

Si j'ai bien compris la notion de base du principe d'équivalence,
c'est que pour un champ de gravitation à symétrie sphérique,
la chute libre d'un cosmonaute depuis l'infini dans un champ de gravitation engendré par une boule à la surface duquel se trouve un astronaute est équivalente à l'accélération d'un astronaute dans un espace-temps libre de tout champ de gravitation vers un cosmonaute stationnaire en apesanteur.
n'est ce pas?

[Nicophil]

Bonjour,

Non, ce que j'ai du mal comprendre, ... mais que le temps peut s'écouler différemment dans deux référentiels inertiels comme vous me le faite savoir.

http://classiques.uqac.ca/classiques...tm#Anchor-3800

En conséquence, les observateurs qui se déplacent avec la tige en mouvement n'affirmeront pas que les horloges sont synchronisées, même si les observateurs dans le système stationnaire témoigneront que les horloges sont synchronisées.

Nous en concluons que nous ne pouvons pas attacher une signification absolue au concept de simultanéité. Dès lors, deux évènements qui sont simultanés lorsque observés d'un système ne seront pas simultanés lorsque observés d'un système en mouvement relativement au premier.

[PPathfindeRR]

à ù100fil,

Tu proposes un lien (représentation), et encore une fois de plus (comme sur wikipédia), je retombe sur une histoire d'accélération !
je cite le passage :

p.47
Afin de rendre l’effet plus frappant, Paul Langevin à mis en scène en 1911 un voyageur qui quitte la Terre à bord d’ « un projectile », voyage vers une étoile à une vitesse voisine de celle de la lumière et revient sur Terre au bout de deux ans, alors qui s’est écoulé 200 ans sur notre planète.
Remarquons que dans le texte de 1911, Langevin ne parle pas explicitement de deux « jumeaux », mais d’un « voyageur » et de « la Terre ».
Par ailleurs, il donne clairement l’explication de la dissymétrie entre les deux en mentionnant l’accélération subie par le voyageur.

à Nicophil,

Dans ton lien on parle d'une tige rigide avec deux horloges synchronisée fixées à ses extrémités qui est en mouvement à vitesse constante par rapport à un observateur.
L'observateur voit que les horloges ne sont pas synchronisées.

Bah oui, c'est normale.
C'est comme l'histoire du train :
Sur le quai, un train passe devant nous à grande vitesse (constante).
Quand le train s'approche, il nous parait plus long qu'il ne l'est.
Quand le train s'éloigne, il nous parait plus court qu'il ne l'est.

Avec des horloge à chaque bout du train, on à le même effet.
Quand le train s'approche, on observe l'arrière du train plus éloigné de l'avant (plus long), une distance plus importante qu'elle ne l'est qui nous fait observer l'horloge plus retardé que celle à l'avant car vue plus loin dans le passé, soit une désynchronisation observé des horloges.
Alors que ces deux horloges sont dans le même référentiel inertiel !

Si le train s'arrête et qu'on va voir ces deux horloges, on constatera qu'elle sont toujours bien synchronisées.

Mais là on parle d'observation, de contraction/dilatation des durée et longueur, et non pas de courbure d'espace-temps lui-même.

je remet un dessin sur le principe du train :

[Nicophil]

Par ailleurs, il donne clairement l’explication de la dissymétrie entre les deux en mentionnant l’accélération subie par le voyageur.

Au niveau des calculs, on peut totalement faire abstraction des accélérations : c'est le changement de référentiel inertiel du jumeau aventureux qui explique la dissymétrie : http://fr.wikipedia.org/wiki/Dilatat..._sym.C3.A9trie

Supposons qu'un observateur n°1 voit, depuis son référentiel inertiel muni d'une horloge (dite n°1) qui y est immobile, une horloge (dite n°2) en mouvement à vitesse constante comme fonctionnant au ralenti.
Alors, par symétrie, un observateur n°2 immobile par rapport à l'horloge n°2 voit l'horloge n°1 comme étant en mouvement à vitesse constante par rapport à son référentiel (dit n°2) et donc comme fonctionnant au ralenti.
Ainsi chacun voit l'horloge de l'autre comme fonctionnant au ralenti. La contradiction semble flagrante si on imagine qu'ils se croisent deux fois : la première fois ils initialisent leurs deux horloges à 0, mais, la seconde fois, quelle horloge sera en retard par rapport à l'autre ?

Le paradoxe n'est qu'apparent car pour qu'il y ait deux rencontres, une des deux horloges a dû changer de référentiel inertiel : la relativité restreinte s'y applique différemment et les calculs montrent que c'est cette horloge qui, à la seconde rencontre, retarde sur l'autre.

Mais là on parle d'observation, de contraction/dilatation des durées et longueurs, et non pas de courbure d'espace-temps lui-même.

Intéressant comme distinction.

[invite6754323456711]

Tu proposes un lien (représentation), et encore une fois de plus (comme sur wikipédia), je retombe sur une histoire d'accélération !

Il est aussi écrit (mes les pages n'apparaissent pas sous les extraits donnés) il ne faudrait pas déduire pour autant que le paradoxe des jumeaux est un phénomène intrinsèquement lié à l'accélération. c'est avant tout le reflet de la dissymétrie des lignes d'univers entre les deux évènement de rencontre. si on donne à l'espace-temp une autre topologie que celle d'un espace affine, alors il est possible d'avoir une différence de durée propre avec les deux ligne d'univers toutes deux à 4-accélération identiquement nulle. Il faut pour cela que l'espace-temps ait une topologie multiplement connexe (tore par exemple ou plus généralement, d'un domaine compact aux conditions au contour périodique). voir article JP Uzan, JP Luminet, R Lehoucq et P. Peter The twin paradox and space topology.

Patrick

[Mailou75]

ce que montre aussi le schéma de Mailou que je remercie au passage

Nop

Je serais curieux de voir ce que donnerait le schéma en considérant J1 fixe dans son référentiel et ensuite J2.

On pourrait... mais ça serait vraiment n'importe quoi (je ne le ferai pas désolé...)

La vitesse de la lumière est le paramètre variable qui détermine pour lequel des jumeaux J1 et J2 le temps propre s'écoule le moins rapidement lors de leur voyage.

"D'une tête dure la nature t'a doté..."

[Zefram Cochrane]

Bonsoir,
Einstein n'est pas super convaincant au sujet de la constance de la vitesse de la lumière.
Cela dit, il n'a pas formulé la nuance entre vitesse locale et vitesse coordonnée la lumière

Cordialement,
Zefram

[PPathfindeRR]

... c'est le changement de référentiel inertiel du jumeau aventureux qui explique la dissymétrie ...

Bah justement c'est ça mon soucis !
Quand on change de référentiel inertiel, on doit forcément se trouver dans un référentiel non inertiel... donc subir une accélération, soit passer d'une vitesse constante à une autre... d'un état à un autre ?!!
et je ne comprend pas pourquoi ça concerne seulement le cadre de la RR et non la RG s'il y a accélération !

mais je crois maintenant savoir ou se trouve mon incompréhension après toute cette discutions !
Ne rigolez pas ! mais qu'est ce que c'est que cette 4-accélération ? est-ce ça cette notion d'accélération caché qu'on m'a répondu sur un autre sujet ?
je ne trouve pas de définition et explication (le principe) en français sur le net.
en tous cas ça reste bizarre pour moi, une accélération c'est une accélération et ça garde la même définition pour moi ! à moins que vous savez m'expliquer ces différents aspects.

[PPathfindeRR]

à Nicophil,

et ma deuxième question :
comment peut-il y avoir accélération sans subir une force de pesanteur ?
pour ne pas subir une force de pesanteur (être en impesanteur), il faut alors forcément que l'espace-temps soit courbé ! comme au voisinage de la Terre et lors d'une chute libre.

[Mailou75]

je ne comprend pas pourquoi ça concerne seulement le cadre de la RR et non la RG s'il y a accélération !

1 - C'est tout l’intérêt de l'exemple de Zef : J1 et J2 subissent les mêmes accélérations/décélérations c'est bien la vitesse constante (RR) qui fait la différence
2- On peut parler d'accélération sans parler le RG pour autant (enfin je crois...)
3 - Tu as raison quand tu dis que c'est celui qui est accéléré qui est le plus jeune, que ce n'est pas qu'une question de mouvement relatif,
c'est lié au choix de l'inertiel (fixe). Celui qui fait demi tour (accélération) est le plus jeune, en effet.