Energie de Planck et cosmos, rien de va plus (pour moi)

[Gilgamesh]

Je confirme bien sûr l'explication #20 de Lansberg

Mais c'est vrai que ce terme de comobile a qqchose de piégeux.


Dans mon explication sur les 4 notions de distance, j'aurais peut-être du rajouter la notion de distance-coordonnée, qui pour moi devrait porter le nom de distance comobile. Une distance qui ne se mesure pas en mètre mais en nombre de graduations. C'est ce qu'on note souvent χ (Chi) dans les bouquins de cosmo.

Prenons deux point, A et B, on dit qu'ils sont comobile si χ = cte, ce qui est l'approximation usuelle.

Par exemple ici χ = 5

A . . . . B

5 quoi ? On s'en fiche, le choix est arbitraire.

Et à ce moment là, la distance propre (souvent appellée comobile d'une façon que je trouve piégeuse) c'est :

D(t) = a(t)χ

a(t), le facteur d'échelle, se mesure alors en mètre/graduation, et c'est lui qui permet de relier le choix arbitraire du système de coordonnée à la réalité physique. Ce facteur d'échelle est une fonction du temps : l'univers est en expansion. Et cette dépendance contient toute la cosmologie : les développement à partir de l'équation d'Einstein permet de relier (le carré de) la dérivée logarithmique de a, c-à-d H² = (da/dt)/a, au contenu énergétique de l'univers (densité d'énergie et pression) à travers les 2 équation de Friedmann.

Bon, un dernier truc : très souvent on utilise a sous forme d'un ratio. Dans les bouquin de cours on utilise par exemple â

â = a/a₀

où a₀ représente le facteur d'échelle aujourd'hui. Et c'est le plus souvent ce ratio qui est utilisé pour exprimer le facteur d'échelle. Faut juste comprendre que le facteur d'échelle ça se joue en deux temps : dimensionné en mètre / graduation, puis rapport adimensionné.
-----

[Gilgamesh]

S'il est bien connu que l'inflation résout le problème de la platitude et de l'homogénéité, c'est la première fois que je lis qu'il explique aussi l’absence de monopole magnétique... ( c'est pas vraiment important (pour moi ) mais si quelqu'un veut expliquer un peu je suis preneur.

Les monopôles magnétiques sont des objets théoriques, jamais observés, assimilables à des particules (sans dimension) qui agissent comme les pôles nord ou sud isolés d'un aimant. Tu sais sans doute qu'il est impossible d'isoler les pôle N et S d'un aimant : si on casse un aimant en deux il se forme deux couples de pôles N et S.

Eh bien il se trouve que l'existence de particules porteuses d'une unique charge magnétique est néanmoins requise par la théorie quantique des champs. Et ça ne s'arrête pas là. La théorie prédit qu'à très haute énergie, en partant d'un niveau grand unifié, comme l'univers refroidit, il devrait s'en former en nombre (abondance initiale ~ 10⁸²/m³).

Les monopôles sont des particules stables. Et ce sont des particules massives, avec une énergie de masse de l'ordre de l'énergie de grand unification. Ils devraient complètement dominer la masse de l'univers actuel. Or, on n'observe pas plus de monopôles magnétiques que de beurre fondu au pôle Nord.

Une des motivation première de l'inflation est de trouver un moyen de diluer complètement ces monopôles après qu'ils se soient formé de sorte de réduire leur démographie à des taux compatibles avec l'observation.

Un note de cours mentionnant le problème des monopôles.
Lecture notes 20: Inflation

[Lansberg]

Mais c'est vrai que ce terme de comobile a qqchose de piégeux.

Dans mon explication sur les 4 notions de distance, j'aurais peut-être du rajouter la notion de distance-coordonnée, qui pour moi devrait porter le nom de distance comobile. Une distance qui ne se mesure pas en mètre mais en nombre de graduations. C'est ce qu'on note souvent χ (Chi) dans les bouquins de cosmo.

Oui, c'est trop souvent confus dans ce qu'on peut lire sur le net ou dans certains bouquins. Je pense aussi que la notion de distance-coordonnée est la notion essentielle à bien comprendre et lui donner une bonne fois pour toutes le nom de distance comobile simplifierait les choses et permettrait effectivement une distinction avec la distance propre.

[pachacamac]

merci.

Pour l'explication sur la distance comobile, je comprend que si on étire une règle le nombre de graduation va rester constant le reste est un peu compliqué pour moi va falloir que j'y réfléchisse...

un truc m'étonne : "dans les bouquins de cours ils utilisent



mais sauf erreur de ma part le facteur d’échelle maintenant a(zéro) est posé égal à 1
donc cela reviendrait à ecrire â = a

Merci aussi pour l'histoire des monopôles, c'est très intéressant et j'ignorais tout de cette histoire sauf que c'est encore Dirac qui a démonter qu'ils devaient exister.

[Gilgamesh]

et une qui me trotte dans la tête depuis un certain temps concernant le reheating

Pièce jointe 468304

Lors de la "désintégration" du champs de l'inflaton qui permet l'expansion puis qui converti son énergie en la création de particules pendant la phase du reheating , je ne comprend pas pourquoi cette dernière phase ( celle du réchauffement ) doit nécessairement se présenter sous forme oscillatoire pour que puisse se créer des particules.

tout éclairage serait bienvenue...

Je ne trouve pas de moyen pédagogiquement parlant, le reheating, c'est ardu

Il faut déjà commencer par comprendre pourquoi on a besoin de l'équation d'un oscillateur amorti pour décrire l'inflation.

Le maître pour ça, c'est Susskind.
Cosmology Lecture 9 (c'est en anglais, forcément.)

Et je laisse quand même ce cours complet écrit (remarquablement complet, il balaye toute la cosmologie moderne), rechercher le chapitre 12 REHEATING AFTER INFLATION

[Gilgamesh]

merci.

donc cela reviendrait à ecrire â = a

Oui, c'est bien ça. Faut pas se formaliser, c'est juste de la notation.

[yves95210]

un truc m'étonne : "dans les bouquins de cours ils utilisent

Pièce jointe 468314

mais sauf erreur de ma part le facteur d’échelle maintenant a(zéro) est posé égal à 1
donc cela reviendrait à ecrire â = a

Sauf que c'est quelque-chose qui est dépendant du modèle : en espace "plat" le choix du facteur d'échelle est libre et le plus simple est de poser a₀=0, mais en toute généralité ce n'est pas le cas. En présence d'une courbure spatiale positive ou négative, a est le rayon de courbure (à un facteur constant près) et ne peut donc pas être choisi arbitrairement, à cause du terme k.c²/a² qui intervient dans l'équation de Friedmann.

[pachacamac]

@Gilgamesh,

Merci pour ces deux très bons liens.

Dans une première lecture rapide du documents cité j'y ai trouvé une réponse qui me satisfait au pourquoi les oscillations du reheating sont nécessaires.

s4.jpg
s3.jpg

effectivement le reheating c'est ardu ( comme le reste de la cosmologie quand c'est vu avec les formules)

Lenny ( Leonard Susskind ), bien que grand pédagogue avait aussi des limites pour la vulgarisation. il écrit par exemple dans son livre " Le paysage cosmique", qui traite de la théorie des (super)cordes, qu'il est incapable d'expliquer avec des mots pourquoi ces théories nécessitent des dimensions supplémentaires. ( Pierre Binétruy avait écrit la même chose dans son livre " A la poursuite des ondes gravitationelles".

Aussi à propos de cet excellent document, l'auteur est très modeste puisqu'il ne donne même pas son nom...

Sinon bien que je ne comprend pas vraiment d'où sortent la plupart des formules et que je suis bien évidemment incapable de les développer ou de résoudre les équations, j'ai au moins la satisfaction de connaitre tous les symboles utilisés à l’exception de deux d'entre eux

s.jpg s2.jpg

Aussi dans le chapitre sur le reheating , il se pose une question un peu similaire à celle qui est à l'origine de ce fils de discussion.

s1.jpg

en tout cas avec ce document j'ai de la lecture pour les longues soirée d'hivers et je vais dés aujourd’hui visionner la lecture 9 du cours de Sussking

Bonne journée.
@++

[pachacamac]

Je ne sais pas pourquoi les images n'apparaissent pas dans le texte, j'ai pourtant fais comme d'habitude..

[pachacamac]

Bonjour yves95210,

Ta remarque explique bien l’intérêt de ce formalisme avec â, mais pour la valeur arbitraire du facteur d’échelle au présent en espace plat, la valeur choisie ne serait t'elle pas 1 plutôt que 0 ?

Parce que d'une part c'est ce qu'on trouve dans de bons livres de vulgarisation, mais surtout dans l'expression de â vu plus haut, on aurait un zéro au dénominateur donc c'est pas cool pour les calculs

[yves95210]

Ta remarque explique bien l’intérêt de ce formalisme avec â, mais pour la valeur arbitraire du facteur d’échelle au présent en espace plat, la valeur choisie ne serait t'elle pas 1 plutôt que 0 ?

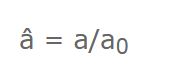
Oups, c'est évidemment une coquille de ma part.

[Gilgamesh]

Note : la remarque de yves est très importante dans le cas de l'inflation. Pour tout applanir de manière à satisfaire la contrainte de courbure nulle - ou quasi - de l'univers dès le Big Bang, idée est bien que le facteur d'échelle (et donc le rayon de courbure) était déjà vertigineusement grand au moment où on fait commencer l'histoire de notre poche d'univers.

[physeb2]

Note : la remarque de yves est très importante dans le cas de l'inflation. Pour tout applanir de manière à satisfaire la contrainte de courbure nulle - ou quasi - de l'univers dès le Big Bang, idée est bien que le facteur d'échelle (et donc le rayon de courbure) était déjà vertigineusement grand au moment où on fait commencer l'histoire de notre poche d'univers.

Il faut faire attention, c'est assez subtile a apréhender. Par exemple l'inflation pourrait être infinie dans les passé, il y a une limite basse mais pas nécessairement de limite haute car on est dans un cas de densité constante du champs d'inflaton.
La limite inférieure dans le modèle standard avec les données actuelles est un expansion du facteur d'échelle d'un facteur 10²⁶ , ce qui est gigantesque. Mais dans les valeurs du facteur deechelle cela fait une transition du type (schematiquement ce ne sont pas les bons chiffres):
a = 0.0000000000000000000000000000 0000001 = 10^-35 à une valeur de a = 0.000000001 = 10^-9
la variation est titanesque mais la valeur du facteur d'échelle à la fin de l'inflation reste quelque chose de petit, qui est définit par ce dont nous avons besoins pour expliquer l'évolution de l'Univers depuis le réheating.

Donc oui l'expansion fut énorme (voir infini) mais ça donnera une valeur de facteur d'échelle a la fin de l'inflation qui est petit. Je comprends ce que tu veux dire Gilgamesh, mais pour ceux qui connaissent pas tès bien, il ne faut pas s'attendre a un facteur d'échelle grand dans l'absolue a la fin de l'inflation

[pachacamac]

@Gilgameh,

Salut,

le facteur d'échelle (et donc le rayon de courbure) était déjà vertigineusement grand

Désolé, je comprend pas ce que tu dis parce que :
1) je n'ais, dans ma petite collection d’équations sur la cosmologie, aucune relation entre le rayon de courbure et le facteur d'échelle.

2) intuitivement, je me dis que si le rayon de courbure était plus petit, ça aurait été encore plus facile à aplanir. Peut être même avec un nombre de e-folding inférieur à


aussi pour

au moment où on fait commencer l'histoire de notre poche d'univers.

Je suis par sur de quel moment tu parles : au début de l'inflation (au début de la phase de slow-roll ou à la fin de l'inflation.

N.B. j'ai visionné la vidéo de Susskink : I got it all il emploie que des équations simples ( niveau terminale) pour expliquer l'inflation.J'y ai aussi compris pourquoi le réchauffement s'appelle ainsi (parce qu'à la fin de l'inflation avant le reheating l'univers était vide et froid ) et pour justifier la nécessité de l'inflation il commence et insiste sur l'histoire de l'abscence des monopôles magnétiques que je connaissais déjà grâce à ton post

[pachacamac]

@physeb2,

merci pour ces précisions.

il ne faut pas s'attendre a un facteur d'échelle grand dans l'absolue

Et on a pas une estimation, même à la louche, de la valeur du facteur d’échelle à la fin de l'inflation ?

[physeb2]

1) je n'ais, dans ma petite collection d’équations sur la cosmologie, aucune relation entre le rayon de courbure et le facteur d'échelle

en fait si tu as ça. La courbure décroit avec le carré du facteur d'échelle dans les équations de Friedmann que tu avais mis en image dans un de tes premiers messages.

2) intuitivement, je me dis que si le rayon de courbure était plus petit, ça aurait été encore plus facile à aplanir. Peut être même avec un nombre de e-folding inférieur à

Non, plus le rayon de courbure est petit et plus la courbure est grande. Une petite sphere (rayon petit) a une courbure plus grande que une grande sphere (rayon plus grand).

Je suis par sur de quel moment tu parles : au début de l'inflation (au début de la phase de slow-roll ou à la fin de l'inflation.

Je pense qu'il se réfère a la fin de l'inflation (fin de reheating)

[physeb2]

Et on a pas une estimation, même à la louche, de la valeur du facteur d’échelle à la fin de l'inflation ?

Si, complètement. Mais il faut que je cherche pour donner la valeur correcte

[yves95210]

1) je n'ais, dans ma petite collection d’équations sur la cosmologie, aucune relation entre le rayon de courbure et le facteur d'échelle.

Si, bien sûr, c'est l'équation de Friedmann avec son terme k/a², k=-1, 0 ou 1 suivant le signe de la courbure.

Cf. par exemple le cours d'introduction à la RG de Gourgoulhon (en accès libre) :


PS : désolé, je n'avais pas vu que physeb avait déjà répondu.

[physeb2]

Dans l'équation de Friedmann, le k ne vaut pas -1,0 ou 1. C'est une valeur non discrète. A ne pas confondre avec le kappa normalisé qui apparait dans la métrique.

[yves95210]

Dans l'équation de Friedmann, le k ne vaut pas -1,0 ou 1. C'est une valeur non discrète. A ne pas confondre avec le kappa normalisé qui apparait dans la métrique.

Toujours selon la même référence (et bien d'autres), la métrique s'écrit effectivement
image_2022-10-17_203526131.png

et l'équation de Friedmann qui en découle,
image_2022-10-17_203641747.png

PS : désolé mais je ne sais toujours pas inclure deux images pour qu'elles s'affichent directement dans le même message...

[physeb2]

Oui c'est un gros problème qui m'a joué bien des tours durant mon doctorat. Le terme dans l'équation de Friedmann:


n'est pas normalisée, cette valeur correspond a la densité d'énergie de courbure et dépend de la densité totale dans la région considérée. Si tu considère 2 sphères de 20 Mpc de rayon centrée sur deux positions différentes dans l'Univers, tu mesure la densité d'énergie a l'intérieur, elles seront normalement différentre (distribution gaussienne pour cette échelle). Donc la densité de courbure va être différente dans les deux cas. Et c'est une variation continue.

Ce qui se passe, est que quand tu change de signe de courbure, la forme de la métrique change. La forme est la même pour toutes les valeurs positives, puis pour toutes les valeurs négatives. Donc on renormalise pour donner la forme, et dans ce cas on a les fameuses valeurs k/|k| = -1, 0, +1, avec le 0 poser à la main quand k=0. Mais k en général est une valeur continue.

[pachacamac]

Heuu.. dans la formule ci-dessous, il y a un k et un kappa normalisé ? je dois être bigleux mais je vois même en regardant bien avec mes lunettes deux fois le même symbole



N.B. après avoir zoommé plusieurs fois peut être different t'il par la largeur de la "boucle" du bas

PS : désolé mais je ne sais toujours pas inclure deux images pour qu'elles s'affichent directement dans le même message...

Oui, il y a un truc bizarre, j'ai deja inclu plusieurs fois des images sans soucis et sur le post #38 de cette discussion en faisant la même chose ( icône image puis parcourir puis ajouter un fichier ) les images ne se sont pas affichées

[yves95210]

Oui c'est un gros problème qui m'a joué bien des tours durant mon doctorat. Le terme dans l'équation de Friedmann:


n'est pas normalisée, cette valeur correspond a la densité d'énergie de courbure et dépend de la densité totale dans la région considérée. Si tu considère 2 sphères de 20 Mpc de rayon centrée sur deux positions différentes dans l'Univers, tu mesure la densité d'énergie a l'intérieur, elles seront normalement différentre (distribution gaussienne pour cette échelle). Donc la densité de courbure va être différente dans les deux cas. Et c'est une variation continue.

Ce qui se passe, est que quand tu change de signe de courbure, la forme de la métrique change. La forme est la même pour toutes les valeurs positives, puis pour toutes les valeurs négatives. Donc on renormalise pour donner la forme, et dans ce cas on a les fameuses valeurs k/|k| = -1, 0, +1, avec le 0 poser à la main quand k=0. Mais k en général est une valeur continue.

Mais quand tu introduis une densité d'énergie et une courbure spatiale variables, tu ne parles plus vraiment du modèle (idéalisé) d'espace-temps spatialement homogène et isotrope (à toute échelle) décrit par la métrique FLRW...

Je suis bien d'accord sur le fait que des sphères distinctes de 20 Mpc de rayon n'ont aucune raison d'avoir des densité d'énergie identiques et que FLRW est une approximation qui ne marche bien qu'à grande échelle (disons à partir de 150 Mpc); ou qu'on peut approximer la géométrie de chacune de ces sphères à l'aide d'une métrique FLRW avec des paramètres locaux (densité d'énergie et de courbure) distincts.
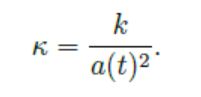
Mais faire varier ces paramètres de manière continue sur tout l'espace, je n'ai jamais vu ça (mais je n'ai pas fait de doctorat ), à part avec la métrique de Lemaître-Tolman (dont FLRW n'est qu'un cas particulier).

Est-ce que tu me donner la référence d'un cours (de préférence accessible en ligne) ou d'une publication (lisible par quelqu'un qui n'a comme bagage que le cours d'intro à la RG de Gourgoulhon, par exemple) où la solution de Friedmann-Lemaître est présentée comme tu le fais ?

[JPL]

Il me semble qu’on a largement dépassé le cadre des questions de base. On a donc le choix de transférer dans Astrophysiciens, physiciens et étudiants avancés ou dans Discussions libres.

[physeb2]

Mais quand tu introduis une densité d'énergie et une courbure spatiale variables, tu ne parles plus vraiment du modèle (idéalisé) d'espace-temps spatialement homogène et isotrope (à toute échelle) décrit par la métrique FLRW...

Pas vraiment, la métrique FLRW assume que a l'intérieur de la sphere a laquelle tu applique. Elle n'assume pas l'homogeneite a toutes les échelles, heureusement, sinon on ne pourrait pas l'utiliser en cosmologie.
Quand tu appliques les équations de Friedmann aux spheres que j'ai mentionné, tu assumes qu'a l'interieur c'est homogene et isotrope et donc que la valeur moyenne de densité est suffisante pour décrire le système. Quand tu l'applique a l'Univers observable tu fais la même hypothese mais a très grande échelle. Lorsque tu pense que cette approximation est inapropriée tu as en effet la metrique de Tolman-Bondi (j'imagine que tu te réfère a cette métrique quand tu dis Lemaitre-Tolman).

En fait ce que je deecris est à la base de la thérorie de la formation des structures en cosmologie. Ça commence avec les travaux de modèle d'éfondrement sphérique de Gunn & Gott 1972, puis la combinaison avec un champs gaussien aléatoire pour donner la fonction de masse des halos par Press & Schechter 1974. Ensuite il y a toute la théorie du biais des halos qui suit cette même approche: "Excursion set" (travaux en particulier de KBond 1991) ou "Peak Baground Split" (Mo & White 1996, Sheth & Tormen 1999, 2001) puis plein de travaux jusqu'a aujourd'hui.

Je te mets une note de Scott Dodelson (l'auteur du livre de cosmologie Modern Cosmology 2003, avec une nouvelle version depuis l'annee derniere avec l'apport de Fabian Schmidt).Les pages 32 a 37 sont les utiles ici, surtout page 36.
Dans cette note tu peux voir nottamment l'equatio 2.46 où apparait explicitement Omega_k dans la forme du calcul des distances. La forme en sinh ou sin resultent de la métrique avec coubure negative et positive (et est la fonction identité en cas de courbure nulle) qui sont exemplifiée avec k=-1, 0, +1. Mais comme tu le vois, la densité intervient de manière directe et cette densité qui est
est une valeur continue et non discrète.



Je te mets quelques pages de thèse en français su la formation de structure basée sur les réfeerences citées avant. Surtout, tu va pouvoir voir comment est noté la densitee de courbure en fonction de la densité moyenne a l'inteerieur de d'une sphère donnée (equations II.30 et II.31):

[physeb2]

Il me semble qu’on a largement dépassé le cadre des questions de base. On a donc le choix de transférer dans Astrophysiciens, physiciens et étudiants avancés ou dans Discussions libres.

Je suis d'accord. Les deux me parraissent bien

[JPL]

Déplacement effectué.

[yves95210]

Pas vraiment, la métrique FLRW assume que a l'intérieur de la sphere a laquelle tu applique. Elle n'assume pas l'homogeneite a toutes les échelles, heureusement, sinon on ne pourrait pas l'utiliser en cosmologie.

On le fait quand-même, dans le modèle LambdaCDM (et dans ses prédécesseurs)...

Et pour l'appliquer à l'intérieur d'une sphère sans se soucier de ce qui se passe à l'extérieur il faut quand-même faire des hypothèses simplificatrices (en gros, supposer que la symétrie sphérique se prolonge suffisamment loin au-delà de la sphère concernée). Par exemple l'approximation par FLRW marche bien pour la partie centrale des vides cosmiques. Pour les grandes zones de sur-densité (dont certaines parties ont commencé à se contracter, ou ont même fini de le faire, produisant les amas de galaxies) on ne peut utiliser FLRW que pour décrire leur géométrie moyenne, comme tu le dis ensuite; mais effectivement, ça peut suffire en cosmologie (même si il y a encore des débats ouverts sur le sujet).

Mais ce n'est pas parce que la métrique a la même expression générale (FLRW) dans tous les domaines sphériques où elle est ainsi utilisée qu'il s'agit de la même métrique FLRW (avec k=-1, 0 ou 1), solution unique de l'équation d'Einstein pour un espace-temps spatialement homogène et isotrope, puisque les valeurs des paramètres a et k sont spécifiques à chacun des domaines sphériques concernés (et dépendent de leurs densités d'énergie, supposées différentes). Il ne s'agit donc pas d'un modèle de Friedmann-Lemaître (avec sa densité de matière uniforme) appliqué à tout l'univers, mais d'un assemblage de modèles de FL distincts, de courbure spatiale positive ou négative, plongés dans un univers moyen décrit par un modèle FL de courbure spatiale (a priori) nulle. Et dans chacun de ces modèles la valeur de k est bien -1, 0 ou 1.

Quand tu appliques les équations de Friedmann aux spheres que j'ai mentionné, tu assumes qu'a l'interieur c'est homogene et isotrope et donc que la valeur moyenne de densité est suffisante pour décrire le système.

Oui, bien sûr.

Quand tu l'applique a l'Univers observable tu fais la même hypothese mais a très grande échelle. Lorsque tu pense que cette approximation est inapropriée tu as en effet la metrique de Tolman-Bondi (j'imagine que tu te réfère a cette métrique quand tu dis Lemaitre-Tolman).

on ne va pas refaire l'histoire, mais Lemaître avait décrit cette solution indépendamment de Tolman (et les deux bien avant que Bondi revisite leurs travaux). Et la métrique est d'ailleurs plutôt connue sous le nom LTB, du moins c'est sous ce nom que je l'ai rencontrée le plus souvent.

Je te mets une note de Scott Dodelson (l'auteur du livre de cosmologie Modern Cosmology 2003, avec une nouvelle version depuis l'annee derniere avec l'apport de Fabian Schmidt).Les pages 32 a 37 sont les utiles ici, surtout page 36.
Dans cette note tu peux voir nottamment l'equatio 2.46 où apparait explicitement Omega_k dans la forme du calcul des distances. La forme en sinh ou sin resultent de la métrique avec coubure negative et positive (et est la fonction identité en cas de courbure nulle) qui sont exemplifiée avec k=-1, 0, +1. Mais comme tu le vois, la densité intervient de manière directe et cette densité qui est
est une valeur continue et non discrète.

Bien sûr que Omega_k n'est pas une valeur discrète, même si k l'est, puisque Omega_k = kc²/(a²H²) et que a varie continument.

Je te mets quelques pages de thèse en français su la formation de structure basée sur les réfeerences citées avant. Surtout, tu va pouvoir voir comment est noté la densitee de courbure en fonction de la densité moyenne a l'inteerieur de d'une sphère donnée (equations II.30 et II.31):

Tu as dû faire une coquille, puisque (en considérant que est la densité d'énergie totale)



Si c'est bien ça que tu veux dire, il n'y a pas de problème.

[yves95210]

Déplacement effectué.

Il faudrait d'ailleurs pouvoir renommer la discussion (par exemple FLRW, rien ne va plus...)

[yves95210]

PS : j'ai voulu faire un petit ajout au message précédent, mais trop tard pour le modifier...

Mais ce n'est pas parce que la métrique a la même expression générale (FLRW) dans tous les domaines sphériques où elle est ainsi utilisée qu'il s'agit de la même métrique FLRW (avec k=-1, 0 ou 1), solution unique de l'équation d'Einstein pour un espace-temps spatialement homogène et isotrope, puisque les valeurs des paramètres a et k sont spécifiques à chacun des domaines sphériques concernés (et dépendent de leurs densités d'énergie, supposées différentes). Il ne s'agit donc pas d'un modèle de Friedmann-Lemaître (avec sa densité de matière uniforme) appliqué à tout l'univers, mais d'un assemblage de modèles de FL distincts, de courbure spatiale positive ou négative, plongés dans un univers moyen décrit par un modèle FL de courbure spatiale (a priori) nulle. Et dans chacun de ces modèles la valeur de k est bien -1, 0 ou 1.

On peut peut-être décrire cet assemblage par une équation "à la FLRW" avec une valeur variable (et non discrète) de k dépendant des coordonnées spatiales, mais ce n'est plus l'équation d'une métrique.