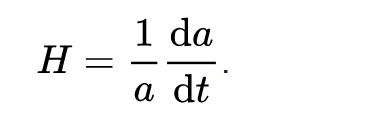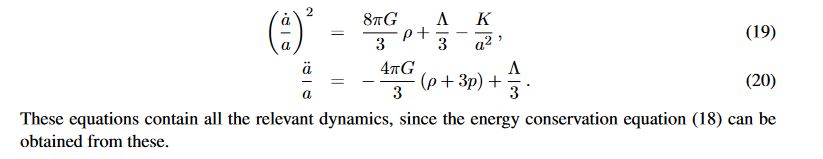Comme déjà dit juché sur vos épaules de savant j'avance à pas de géant.
Donc pourquoi ne pas essayer de comprendre vraiment l'équation de Friedmann Lemaître Walker
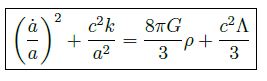
le membre de droite de l'équation ne me semble pas poser de problème.
A gauche, je reconnais maintenant le terme lié à la courbure par contre (la dérivée de a) /a me pose problème.
Je crois savoir que le facteur d'échelle et la densité sont des fonctions du temps.
a =f(t)
rho = f'(t)
donc faut t'il comprendre les "a " de l'équation comme des valeurs à l'instant t ?
Merci
note 1 : c'est pas trop une question d’étudiant avancé en astrophysique mais j'avoue que j'ai encore quelques grosses lacunes en ce domaine...
note 2 : à propos de l'extrait de thèse proposé par physeb2, ça me fait plaisir de voir que c'est celle de Sébastien Fromentaux. Celui -ci fût en 2015 l'un des formateurs le plus prolixe dans le FLOT/MOOC : Gravité! du Big-Bang aux trous noirs organisé par l'APC
-----





 représente la moyenne de la variable
représente la moyenne de la variable 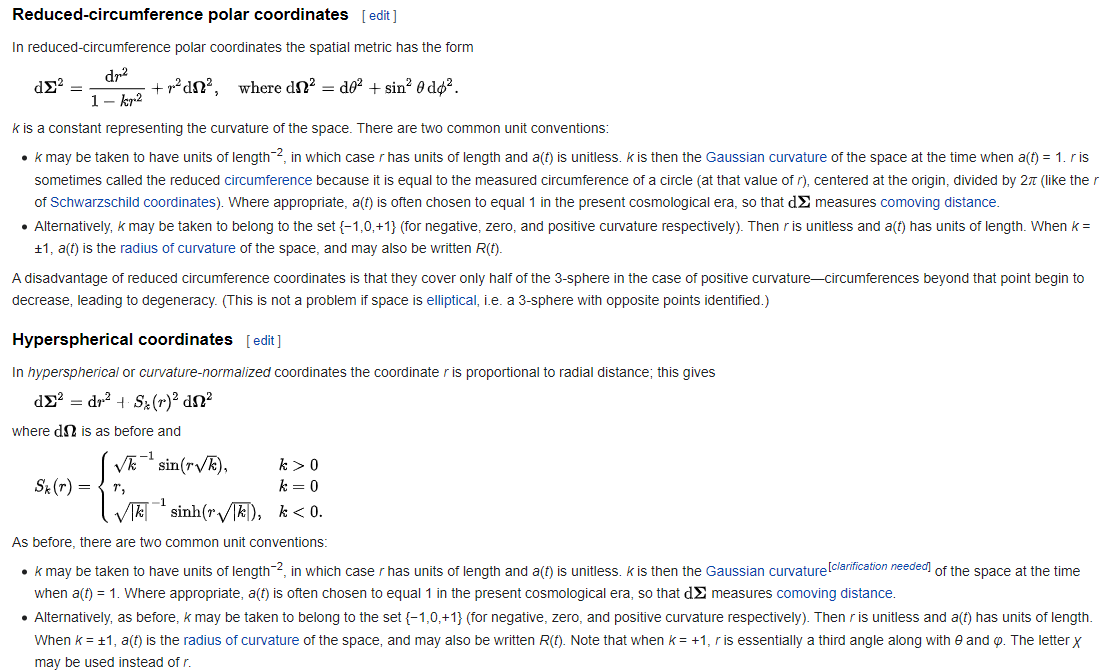
 (désolé la modération....)
(désolé la modération....)