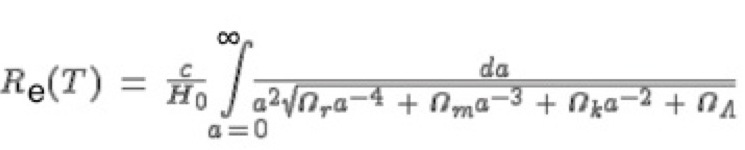Redshift - dualité variable temporelle et spatiale - Calcul des BAO

[Lansberg]

Bonjour,

il ne s'agit pas exclusivement d'observations proches (c'est d'ailleurs plus compliqué par le brassage matière baryonique-matière noire) mais dans l'absolu de mesures qui concernent l'univers depuis le CMB. L'expérience CHIME s'intéresse aux BAO jusqu'à z~2,5.
La formule ("racine cubique...") permet de calculer la position du pic d'une BAO quand il n'y a pas suffisamment de données pour réaliser des analyses séparées le long et transversalement à la ligne de visée (dz et d-théta de la figure 1.6 du message initial de Fabio).
-----

[Mailou75]

Salut,

Je croyais que les BAO étaient des ondes physiques, visibles dans les irrégularités du CMB. Qu’on pouvait voir ces ondes fossilisées correspondant à une date (380.000ans) uniquement car le plasma pouvait transporter des ondes physiques. Dès lors que les éléments s’éloignent, créant du vide entre eux, il ne peut plus y avoir de transport d’ondes, sinon électromagnétiques. Donc à des z inférieurs à 1100 je me demande bien ce qu’on observe...

Bref, ce que je connais du sujet ce limite à peu près à ça, alors si ce peu est faux j’y comprends plus rien

[yves95210]

Salut,

Je croyais que les BAO étaient des ondes physiques, visibles dans les irrégularités du CMB. Qu’on pouvait voir ces ondes fossilisées correspondant à une date (380.000ans) uniquement car le plasma pouvait transporter des ondes physiques. Dès lors que les éléments s’éloignent, créant du vide entre eux, il ne peut plus y avoir de transport d’ondes, sinon électromagnétiques. Donc à des z inférieurs à 1100 je me demande bien ce qu’on observe...

On observe les traces qu'ont laissé ces ondes, figées lors de la recombinaison, dans la distribution de matière de l'univers observable. Les pics de densité de matière présents à cette époque (celle du CMB) ont permis la création des structures qu'on connaît dans l'univers récent, galaxies, amas, etc.
Lorsqu'on mesure les distances entre chaque paire de galaxies sur un grand nombre d'entre elles, et qu'on trace une courbe représentant la probabilité que deux galaxies soient séparées par une distance comobile D, on constate sur cette courbe une bosse correspondant au "sound horizon" des BAO (cf. https://en.wikipedia.org/wiki/Baryon...tal_Sky_Survey, et pour plus de détails sur la fonction de corrélation, https://en.wikipedia.org/wiki/Correl...on_(astronomy)).

(source)

[Lansberg]

Et pour le graphique présenté ci-dessus, les différentes couleurs correspondent à des z différents.
Les BAO constituent ainsi un étalon de distance. Leur dimension est connue (~150 Mpc) ce qui permet de tester l'expansion de l'univers. Grâce à leur géométrie "sphérique" on sait qu'elles ont la même dimension transversalement et radialement. D'où les mesures de ∆théta pour calculer la Da et ∆z pour calculer H(z).
Le test statistique d' Alcock-Paczynski associé à la 2pCF (two-point autocorrelation function = mesures de distance entre paires de galaxies) permet de contraindre les paramètres cosmologiques (H(z) ; Ωm...). Si les paramètres cosmologiques sont faux alors la symétrie sphérique des BAO n'est plus respectée. Il y a des déformations radiale ou transversale. Il faut donc ajuster ces paramètres pour avoir la bonne géométrie, ce qui permet de comparer ces paramètres avec ceux issus de l'étude du CMB.
Il faut aussi tenir compte des déformations engendrées par les vitesses particulières des galaxies (à cause de la gravitation) qui se répercutent sur les ∆z mesurés (RSD = redshift space distorsion).

[fabio123]

Il suffit de raisonner en distances radiales (et transverses) comobiles, non ?
Dans ce cas la différence entre les distances de tes 2 extrémités est la distance que tu mesurerais à l'époque actuelle, i.e. sur l'hypersurface spatiale à t₀=aujourd'hui, si c'était physiquement possible d'effectuer une telle mesure. Et cela vaut aussi bien pour la distance transverse que pour la distance radiale.

Si tu ne l'as pas déjà fait, jette un coup d’œil à ce papier, dont j'extrais la citation ci-dessous :

Désolé de ne reprendre ce post que maintenant, j'ai débranché pendant les vacances.

Salut Yves95210,

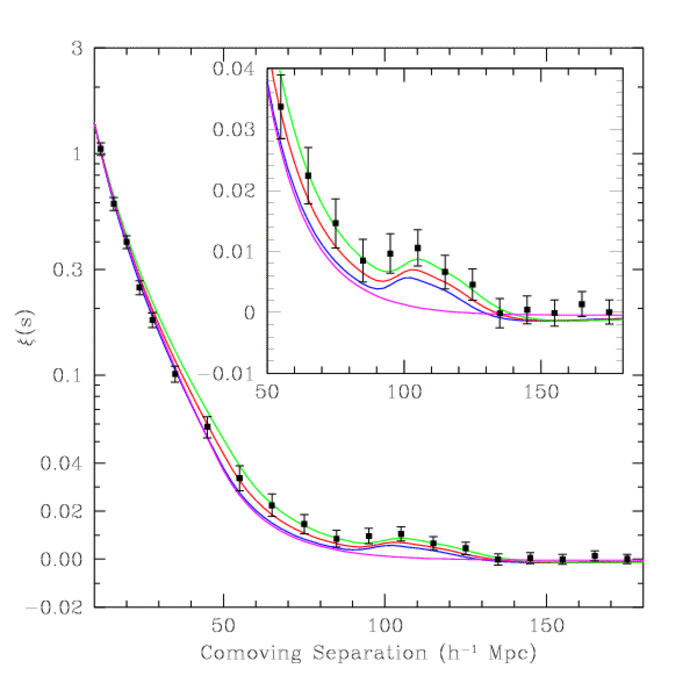
je pense que ton approche/raisonnement est le plus simple pour comprendre ma difficulté à me représenter concrètement le calcul de la taille des BAO avec un en profondeur, c'est-à-dire entre le z le plus proche et le z le plus éloigné.

En effet, quand je raisonne avec des distances comobiles, on tient compte d'un seul moment : le temps d'aujourd'hui (z=0) et il est ainsi plus facile de se dire :

1) "actuellement, les BAO sont supposées avoir une symétrie sphérique (depuis même le découplage ou alors peut-être que cette symétrie a été déformée par l'expansion et la formation des structures ?)"

2) "on sait qu'il y a un bump dans la fonction de corrélation à 2 points entre 100 et 150 h^-1 Mpc" (ceci a été calculé d'après différents survey comme SDSS ou autres)

3) Cette distance comobile entre galaxies privilégiée étant assez bien connue, on peut calculer cette distance à l'époque du découplage (on appelle ça une distance propre à z = 1100 ?) qui donne normalement : 150/1100 ~ 0.15 h^-1 Mpc. Si j'emploie le bon vocabulaire, on peut dire que la distance privilégiée entre les différentes fluctuation du plasma baryon-photon à z > 1100 (ou alors la taille de la fluctuation elle-même, je ne sais pas bien encore faire la différence entre les 2) et figée au moment du découplage, est égale à 0.15 h^-1 Mpc : ce calcul est-il correct ?

Par ailleurs, j'aimerais avoir un petit rappel sur certaines définitions pour ne pas louper d'épisode dans vos explications :

1) Ce que l'on appelle le "sound horizon", est-ce tout simplement la taille comobile des BAO (150 h^-1 Mpc) ?

2) La distance diamètre angulaire D_a est-elle la distance, pour un redshift donné, à l'époque où a été émise la lumière que nous recevons maintenant (lumière émise par l'objet qui a ce redshift donné) ?

3) L'horizon cosmologique, c'est-à-dire le point le plus éloigné depuis lequel nous recevons de la lumière aujourd'hui correspond environ à 46 Giga a.l. La distance diamètre angulaire de cet horizon vaut donc : 46/1100 ~ 42 Millions a.l ~ 13 Mpc :

autrement dit, si nous avions existé à cette époque (tiré là aussi par les cheveux), nous aurions été à 13 Mpc d'un objet émettant de la lumière juste après le découplage (encore tiré par les cheveux, désolé, c'est juste pour la compréhension) : est-ce correct ?

4) Et de manière générale, la relation entre la distance comobile (distance actuelle, c'est-à-dire pour le même "temps cosmique") et distance diamètre angulaire est bien : D_a = D_c/(1+z) ?

5) Quelle était le rayon de l'Univers au moment du découplage : naïvement, on pourrait dire : Rayon = c/H0 ~ 3000 h^-1 Mpc ? (c'est pour ça peut-être qu'on emploie les termes sub/super Hubble dans le domaine du CMB ?)

Merci à tous pour vos réponses, je dois encore étudier la question avec tous les liens qui m'ont été donnés et je reviendrai sur ce post si besoin est.

[Mailou75]

Réponses en bleu

2) La distance diamètre angulaire D_a est-elle la distance, pour un redshift donné, à l'époque où a été émise la lumière que nous recevons maintenant (lumière émise par l'objet qui a ce redshift donné) ?

Oui, une image figée à la date et lieu d'émission nous parvient telle quelle aujourd'hui.

3) L'horizon cosmologique, c'est-à-dire le point le plus éloigné depuis lequel nous recevons de la lumière aujourd'hui correspond environ à 46 Giga a.l. La distance diamètre angulaire de cet horizon vaut donc : 46/1100 ~ 42 Millions a.l ~ 13 Mpc :

Oui, c'est la distance à laquelle se trouvait, à 380.000 ans, la zone qui a émis le CMB qu'on voit aujourd'hui.

autrement dit, si nous avions existé à cette époque (tiré là aussi par les cheveux), nous aurions été à 13 Mpc d'un objet émettant de la lumière juste après le découplage (encore tiré par les cheveux, désolé, c'est juste pour la compréhension) : est-ce correct ?

Oui, ensuite le photon s'éloigne, emporté par l'espace en expansion, et se rapproche quand le taux d'expansion décroit.

4) Et de manière générale, la relation entre la distance comobile (distance actuelle, c'est-à-dire pour le même "temps cosmique") et distance diamètre angulaire est bien : D_a = D_c/(1+z) ?

Oui, et Dl=Da(z+1)^2 où Dl est la distance de luminosité.

5) Quelle était le rayon de l'Univers au moment du découplage : naïvement, on pourrait dire : Rayon = c/H0 ~ 3000 h^-1 Mpc ? (c'est pour ça peut-être qu'on emploie les termes sub/super Hubble dans le domaine du CMB ?)

La taille (comobile, Dc) de l'univers visible était de 42 millions d'Al à 380.000 ans.

[fabio123]

5) Quelle était le rayon de l'Univers au moment du découplage : naïvement, on pourrait dire : Rayon = c/H0 ~ 3000 h^-1 Mpc ? (c'est pour ça peut-être qu'on emploie les termes sub/super Hubble dans le domaine du CMB ?)

La taille (comobile, Dc) de l'univers visible était de 42 millions d'Al à 380.000 ans.

Tu veux sans doute dire 42 milliard d'Al à z = 1100 ? (si on intègre "c/H(z) dz" de z=0 jusqu'à z = 1100 ?)

[fabio123]

mea culpa sur mon post ci-dessus, (je suis allé un peu trop vite) : tu obtiens ce résultat en appliquant un facteur 1/1100 sur la Dc 44 G Al ?

[Mailou75]

mea culpa sur mon post ci-dessus, (je suis allé un peu trop vite) : tu obtiens ce résultat en appliquant un facteur 1/1100 sur la Dc 44 G Al ?

Oui c'est ça, tu as toi même déjà fait le calcul, pour le CMB :
Dc=46Gal, Da=42Mal et z+1=1100 avec le rapport Dc=Da(z+1)

[Lansberg]

Bonjour,

1) "actuellement, les BAO sont supposées avoir une symétrie sphérique (depuis même le découplage ou alors peut-être que cette symétrie a été déformée par l'expansion et la formation des structures ?)"

Les BAO sont sphériques.
Les déformations éventuelles sont liées d'une part aux paramètres cosmologiques du modèle en vigueur qui peuvent être erronées. L'intérêt de l'étude des BAO, via le test statistique d'Alcock Paczynski, est justement d'apporter les corrections sur H(z) (mesure de ∆z selon la ligne de visée) et Da(z) (mesure de l'angle ∆théta selon la direction transverse) pour que les BAO conservent cette sphéricité.
D'autre part les déformations sont liées aux vitesses particulières des galaxies de la BAO (Vpec) dues aux interactions gravitationnelles (effet RSD=redshift space distorsion).

2) "on sait qu'il y a un bump dans la fonction de corrélation à 2 points entre 100 et 150 h^-1 Mpc" (ceci a été calculé d'après différents survey comme SDSS ou autres)

Oui. A ce sujet cet article intéressant cité dans un autre fil de discussion concernant les derniers résultats du SDSS : https://www.techno-science.net/actua...rs-N19820.html

3) Cette distance comobile entre galaxies privilégiée étant assez bien connue, on peut calculer cette distance à l'époque du découplage (on appelle ça une distance propre à z = 1100 ?) qui donne normalement : 150/1100 ~ 0.15 h^-1 Mpc. Si j'emploie le bon vocabulaire, on peut dire que la distance privilégiée entre les différentes fluctuation du plasma baryon-photon à z > 1100 (ou alors la taille de la fluctuation elle-même, je ne sais pas bien encore faire la différence entre les 2) et figée au moment du découplage, est égale à 0.15 h^-1 Mpc : ce calcul est-il correct ?

Oui c'est l'ordre de grandeur des BAO au découplage (~ 0,15 Mpc ).

Par ailleurs, j'aimerais avoir un petit rappel sur certaines définitions pour ne pas louper d'épisode dans vos explications :

1) Ce que l'on appelle le "sound horizon", est-ce tout simplement la taille comobile des BAO (150 h^-1 Mpc) ?

Oui, la trace "fossilisée" en quelque sorte.

[fabio123]

Bonjour,

merci à tous pour vos explications.

Cependant, j'aimerais avoir encore quelques précisions.

On sait que l'angle sous lequel sont vues les BAO ne change pas entre aujourd'hui et au temps de la recombinaison.

Si j'admets aujourd'hui que la taille comobile des BAO est d'environ 150 h^-1 Mpc à z =0.

1) Comment prouver que leur taille à l'époque de la recombinaison valait : 150/1100 ~ 130 h^-1 kpc ?


2) Normalement, cette simple division par (1+z) apparaît dans la relation entre la distance comobile (distance d'un objet aujourd'hui) et la distance diamètre angulaire (distance lorsque la lumière a été émise
par un "objet") ? ; de cette manière, le rayon de l'univers observables au moment du découplage est égal à :

R(z=1100) = 44 G a.l / 1100 = 44 M a.l ~ 13.5 Mpc

3) L'angle theta sous lequel on voit les BAO est constant en faisant le ratio : tan(theta) ~ theta = Taille_BAO(z donné) / Distance_diamètre_angulaire(z) (d'ailleurs, ça serait intéressant de pouvoir le démontrer, on pourrait imaginer un angle qui varie durant l'histoire cosmique)

Comment en déduire la distance diamètre angulaire des BAO à z = 1100, c'est-à-dire à quelle distance un "observateur" (je sais, il n'y avait personne à cette époque, il est hypothétique) se trouverait
lorsqu'il observerait les BAO de taille 130 h^-1 kpc ?

Toutes remarques sont les bienvenues, j'ai encore quelques confusions.

[Gilgamesh]

On sait que l'angle sous lequel sont vues les BAO ne change pas entre aujourd'hui et au temps de la recombinaison.

Bah non, Θ_BAO est une fonction du redshift.

source : Measuring the transverse baryonic acoustic scale from the SDSS DR11 galaxies

[Lansberg]

1) Comment prouver que leur taille à l'époque de la recombinaison valait : 150/1100 ~ 130 h^-1 kpc ?

Ce sont les données du spectre de puissance du CMB qui apportent les informations avec les pics des différentes "oscillations".
La distribution des points chauds et des points froids du CMB se traduit dans le spectre de puissance par des pics (et des creux) acoustiques à cause de leur origine physique. La forme, la taille et la position de ces pics dépendent de nombreux paramètres cosmologiques (ce qui, inversement, permet de les évaluer à partir du spectre de puissance observé).
L'étude des BAO commence donc par l'étude des pics du CMB.
Et on déroule ensuite le cours de l'histoire en fonction du modèle d'univers choisi. Comme cela a déjà été précisé plus haut on peut contraindre le modèle en question (valeur de H(z) entre autres) avec les observations à des z différents.

[Lansberg]

Comment en déduire la distance diamètre angulaire des BAO à z = 1100, c'est-à-dire à quelle distance un "observateur" (je sais, il n'y avait personne à cette époque, il est hypothétique) se trouverait
lorsqu'il observerait les BAO de taille 130 h^-1 kpc ?

Petite rectification : Rs ~100 kpc/h soit 130 kpc.

La question n'a pas trop de sens il me semble. C'est comme si on demandait : à quelle distance se trouve-t-on "actuellement" des BAO de 150 Mpc ?

[fabio123]

Bonsoir,

Petite rectification : Rs ~100 kpc/h soit 130 kpc.

La question n'a pas trop de sens il me semble. C'est comme si on demandait : à quelle distance se trouve-t-on "actuellement" des BAO de 150 Mpc ?

1) Rs représente ce que l'on appelle "l'horizon sonore" ? , c'est-à-dire d'après ce que j'ai vu sur Wikipedia, "la distance maximale parcourue par une onde sonore entre le Big Bang et une époque donnée."

quand on parle de Rs ~ 100 kpc/h, on parle de quelle époque ? de celle de la recombinaison.

2) Je sais qu'il y a depuis pas mal de temps des tensions sur la valeur de H0 mais on peut quand même dire que ça tourne autour de H0 ~70 km/s/Mpc. Quelle est donc l'estimation la plus utilisée
aujourd'hui pour la taille comobile des BAO : 150 Mpc ?

3)

L'angle theta sous lequel on voit les BAO est constant en faisant le ratio : tan(theta) ~ theta = Taille_BAO(z donné) / Distance_diamètre_angulaire(z) (d'ailleurs, ça serait intéressant de pouvoir le démontrer, on pourrait imaginer un angle qui varie durant l'histoire cosmique)

Je pense que j'ai mal expliqué ici : l'angle sous lequel est vu un objet de taille "d" (de préférence fixe dans le temps, en tout cas pour que je comprenne mieux dans un premier temps, mais ce n'est pas forcément un bon cas car par exemple, la taille des BAO change au cours du temps) par rapport un observateur ayant une distance diamètre angulaire "Da(z)" est égale, une fois que cet observateur reçoit les photons émis par l'objet, à :

theta_objet = d / Distance_diamètre_angulaire(z)

Par distance diamètre angulaire, j'entends la distance à l'époque "z" entre l'observateur (en fait, nous mêmes en tant qu'observateurs comobiles) et l'objet observé (dont les photons seront reçu par l'observateur bien après) ?

4) Par exemple, quand on calcule l'horizon cosmologique, c'est-à-dire la taille de l'Univers observable, il a fallu 13.7 G a.l pour qu'un photon d'un objet située actuellement à environ 44 G a.l ait pu nous atteindre. On conclu alors que nous étions à une distance de 44 / 1100 G a.l de cet objet quand il a émis les premiers photons qui nous atteignent aujourd'hui : êtes-vous d'accord ?

On peut écrire : distance_diametre agulaire = R_1 r1 = R_1/R_0 * R_0 r1 = R0 r1 / (1+z) = distance_comobile_objet_observ é / (1+z) avec R_0 le facteur d'échelle d'aujourd'hui, R_1 le facteur à "z" donné et r1 la coordonnée comobile de l'objet calculé avec l'intégrale de

5) Ce que je croyais avoir compris n'est pas forcément bien acquis : le pic "Doppler" du CMB (le premier pic) a une taille environ de 1° (1 degré) ou à l = 200. est-ce que ça correspond au ratio entre la taille des BAO à cette époque (z=1100) et la taille de l'univers observable à cette même époque ?

Ou alors au ratio entre la taille des BAO à z=1100 et (R1 r1), c'est-à-dire : theta_pic_doppler = taille_BAO(z=1100)/ (44 G.al / 1100) ?

6) D'ailleurs, comment est calculé cette taille des BAO de 130 kpc au moment du découplage ?

Comme vous le voyez, c'est confus car il me semble avoir vu quelque part qu'un angle (de quel type d'objet ? je ne sais pas) est conservé entre l'époque de la recombinaison et aujourd'hui mais je ne me souviens plus exactement pourquoi cet angle est conservé. S'il est conservé, ça suppose que le numérateur et le dénominateur changent au cours du temps cosmique.

Désolé d'être un peu insistant mais je tiens à essayer de bien comprendre toutes ces notions.

Merci par avance.

[Lansberg]

Bonjour,

quand on parle de Rs ~ 100 kpc/h, on parle de quelle époque ? de celle de la recombinaison.

Oui.

2) Je sais qu'il y a depuis pas mal de temps des tensions sur la valeur de H0 mais on peut quand même dire que ça tourne autour de H0 ~70 km/s/Mpc. Quelle est donc l'estimation la plus utilisée
aujourd'hui pour la taille comobile des BAO : 150 Mpc ?

C'est l'ordre de grandeur.
La valeur la plus précise obtenue à partir des données de la mission Planck est : rs = (144,71 +/- 0:60) Mpc

3)

Je pense que j'ai mal expliqué ici : l'angle sous lequel est vu un objet de taille "d" (de préférence fixe dans le temps, en tout cas pour que je comprenne mieux dans un premier temps, mais ce n'est pas forcément un bon cas car par exemple, la taille des BAO change au cours du temps) par rapport un observateur ayant une distance diamètre angulaire "Da(z)" est égale, une fois que cet observateur reçoit les photons émis par l'objet, à :

theta_objet = d / Distance_diamètre_angulaire(z)

Par distance diamètre angulaire, j'entends la distance à l'époque "z" entre l'observateur (en fait, nous mêmes en tant qu'observateurs comobiles) et l'objet observé (dont les photons seront reçu par l'observateur bien après) ?

A toute époque Théta(s) = Rs / Da(z) (l'angle est conservé en espace plat).
On connaît Théta(s) avec une bonne précision à partir du CMB. C'est une des données cosmologiques directe.
Théta(s) = (1,04131 +/- 0,00062) x 10^-2 pour l = PI / théta(s) = 3,14 / 0,0104131 ~ 300

Pour z=0, la Da c'est aussi la distance propre en espace plat (bonne approximation de la courbure) soit ~ 45 Gal ~ 13800 mpc
On retrouve bien à la louche, Rs = théta(s) x Da(z) ~ 1,04131 x 13800 = 143,7 Mpc très proche de la valeur citée plus haut.

Bien sûr si on prends la Da pour z=1100 on trouve Rs à cette époque (~ 130 kpc).

[fabio123]

Bonjour,

@Lansberg, merci pour ta réponse.

1) Quand tu écris :

A toute époque Théta(s) = Rs / Da(z) (l'angle est conservé en espace plat).
On connaît Théta(s) avec une bonne précision à partir du CMB. C'est une des données cosmologiques directe.
Théta(s) = (1,04131 +/- 0,00062) x 10^-2 pour l = PI / théta(s) = 3,14 / 0,0104131 ~ 300

que représente la variable "s" dans "Théta(s)" : le "s" de "sound horizon" ?

2) D'autre part, tu dis que l'angle Théta est conservé en espace plat : ça veut dire qu'il y a simplement une relation de proportionnalité entre le sound horizon et la distance diamètre angulaire pour une courbure nulle ?

@Gilgamesh :

Bah non, ΘBAO est une fonction du redshift.

source : Measuring the transverse baryonic acoustic scale from the SDSS DR11 galaxies

Quelle est la courbure prise sur le graphique donné sur ton lien, sphérique, hyperbolique ? (en tout cas, pas plat car sinon, il est constant en espace plat d'après la remarque de @Lansberg ?)


3) Quand on parle d'un observateur dans le passé qui se trouvait à une distance diamètre angulaire donnée par rapport à un objet qui commence à émettre des photons, ceci veut-il dire que nous
ne recevons ces photons que maintenant, c'est-à-dire à z =0 OU ALORS est-ce que ces photons ont déjà été reçus par l'observateur à l'époque où il se situait à cette distance diamètre angulaire. J'ai du mal à conceptualiser un angle theta ~tan(theta) sous lequel serait vu un objet à une certaine époque, si ces photons n'ont pas encore été reçus par l'observateur à cette époque identifé par le redshift "z".

4) a) Dans ma question (où le sound horizon doit être pris comme égal à 100 h^-1 Mpc et non 150 h^-1 Mpc) :

Si j'admets aujourd'hui que la taille comobile des BAO est d'environ 150 h^-1 Mpc à z =0.

1) Comment prouver que leur taille à l'époque de la recombinaison valait : 150/1100 ~ 130 h^-1 kpc ?

Pour calculer la taille du "sound horizon" à l'époque de la recombinaison, je ne comprends le résultat (150/1100) que si je me sers du caractère sphérique des BAO. En effet, je comprends assez facilement que la taille transverse à z =1100 est égale à 100 h^-1 Mpc/1100 = tan(angle de la taille_BAO_a_la_recombinaison) * Distance_diamètre_angulaire(z= 1100).

Si l'angle est conservé, on aurait : tan(angle de la taille_BAO_a_la_recombinaison vu par un observateur situé à D_c/1100) = tan(angle_BAO_aujourdhui obervé par nous à z=0) ?

avec Distance_diamètre_angulaire(z= 1100) = D_c / 1100 ~ 42 M a.l ~ 13 Mpc

Donc pour finir, si je suppose la symétrie sphérique, je peux faire le calcul pour la taille radiale : taille_BAO_recombinaison = 100 h^-1 Mpc / 1100 ~ 0.1 h^-1 Mpc = 100 h^-1 kpc.

Est-ce que ce raisonnement est bon ? J'essaie de comprendre ça parce que le calcul direct 100 h^-1 Mpc / 1100 pour la taille radiale des BAO n'est pas une évidence pour moi, je comprends mieux
le calcul avec la taille transverse.

4) b) "taille_BAO_recombinaison" se nomme alors "sound horizon à z = 1100" ~ 100 h^-1 kpc ?

Mais comme vous l'avez mentionné, la symétrie sphérique peut être perturbée par les effets RSD (redshift space distortions) comme l'effet Kaiser (grandes échelles) ou Finger of God (petites échelles).

Désolé si c'est pas très clair, le sujet est assez difficile pour moi à appréhender, donc vos réponses ou remarques sont les bienvenues.

[Lansberg]

que représente la variable "s" dans "Théta(s)" : le "s" de "sound horizon" ?

Oui.

2) D'autre part, tu dis que l'angle Théta est conservé en espace plat : ça veut dire qu'il y a simplement une relation de proportionnalité entre le sound horizon et la distance diamètre angulaire pour une courbure nulle ?

Oui puisque Da(z) . théta(s) = Rs

4) a) Dans ma question (où le sound horizon doit être pris comme égal à 100 h^-1 Mpc et non 150 h^-1 Mpc) :

Oui

Pour calculer la taille du "sound horizon" à l'époque de la recombinaison, je ne comprends le résultat (150/1100) que si je me sers du caractère sphérique des BAO. En effet, je comprends assez facilement que la taille transverse à z =1100 est égale à 100 h^-1 Mpc/1100 = tan(angle de la taille_BAO_a_la_recombinaison) * Distance_diamètre_angulaire(z= 1100).

[B]Si l'angle est conservé, on aurait : tan(angle de la taille_BAO_a_la_recombinaison vu par un observateur situé à D_c/1100) = tan(angle_BAO_aujourdhui obervé par nous à z=0) ?[B]

L'angle est le même donc la tan aussi, forcément

avec Distance_diamètre_angulaire(z= 1100) = D_c / 1100 ~ 42 M a.l ~ 13 Mpc

42Mal c'est la Da des régions qu'on observe sous forme du CMB aujourd'hui. Ce ne sont pas les BAO.

Donc pour finir, si je suppose la symétrie sphérique, je peux faire le calcul pour la taille radiale : taille_BAO_recombinaison = 100 h^-1 Mpc / 1100 ~ 0.1 h^-1 Mpc = 100 h^-1 kpc.

Oui, ça correspond aux BAO à la recombinaison.

4) b) "taille_BAO_recombinaison" se nomme alors "sound horizon à z = 1100" ~ 100 h^-1 kpc ?

Oui.

[fabio123]

Bah non, Θ_BAO est une fonction du redshift.

source : Measuring the transverse baryonic acoustic scale from the SDSS DR11 galaxies

Salut Gilgamesh,

j'ai quelques soucis concernant ta figure.

1) D'après ce que j'ai cru comprendre, l'angle sous lequel on voit les BAO aujourd'hui n'est pas le même selon cette figure, par exemple entre le ratio (taille_BAO_recombinaison)/(distance_diametre_angulaire_r ecombinaison) et le ratio (taille_BAO_comobile)/(distance_comobile).

Je ne comprends pas pourquoi cet angle n'est pas conservé pour toute valeur du redshift z

Par exemple, on dit souvent que l'Univers avait une taille de 44 G a.l/1100 au moment de la recombinaison, ce qui fait à peu près 40 M a.l à l'époque.

2) Petite précision : l'horizon sonore comobile a une taille environ de 100 h^-1 Mpc : mais parle t-on de du rayon du BAO supposé idéalement sphérique ou alors de son diamètre ?

3) Question similaire pour le CMB : le pic doppler dand le spectre de puissance angulaire est à peu près situé au multipôle l ~200 , ce qui fait ~ 1 degré : Mais là aussi, est-ce cet angle correspond au ratio entre le diamètre (ou rayon là aussi c'est pas clair ?) de l'horizon sonore (pas besoin de préciser BAO ?) qui valait à l'époque 100 h^-1 kpc et le diamètre de l'Univers à z = 1100 (soit 40 M a.l) :

un calcul très simple donne : theta = (0.1*3.26)/ 40*180/pi ~ 0.46 degrès

Comme vous le voyez, il me manque un facteur 2 pour arriver à la valeur de 1° correspondant au pic doppler.

Si quelqu'un pouvait me dire ce qui ne va pas dans ce petit calcul

4) Gilgamesh : sur la figure que tu as mise, tu considère un univers non plat, non ? parce qu'en espace-plat, l'angle ne doit pas changer entre l'époque du CMB et aujourd'hui.

Si je prends theta(bao) = diametre_bao(z)/distance_diametre_angulaire(z) et que cet angle theta(bao) n'est pas constant, c'est que le diamètre (ou rayon ?) des BAO fonction de z n'est pas linéaire avec la distance_diametre_agulaire(z), même dans un espace euclidien ou quasi-euclidien ?

5) comme tu peux voir, je fais des confusions entre la constance (ou plutôt sa variation d'après ta figure) d'un angle sur un "grumeau" sur le CMB et la constance de l'angle du pic Doppler

Tes éclaircissements, si tu peux, m'aideront beaucoup dans ces confusions.

Merci

[Lansberg]

Bonjour,

Par exemple, on dit souvent que l'Univers avait une taille de 44 G a.l/1100 au moment de la recombinaison, ce qui fait à peu près 40 M a.l à l'époque.

Non. Cela correspond à la distance propre des régions de l'espace qui sont à l'origine du CMB observé aujourd'hui.

[yves95210]

4) Gilgamesh : sur la figure que tu as mise, tu considère un univers non plat, non ? parce qu'en espace-plat, l'angle ne doit pas changer entre l'époque du CMB et aujourd'hui.

A titre d'exemple (simplifiant le calcul), tu peux regarder ce qui se passe dans un espace-temps d'Einstein-de Sitter, avec Ω_m=1, Ω_k=0 et Ω_Λ=0.

La distance transverse comobile est alors simplement D_M=D_C (espace plat), et D_C se calcule analytiquement :

avec
donne simplement
et

Je ne colle pas la courbe ici, tu la trouveras dans la figure 2 de "Distance measures in cosmology" (ainsi que la courbe D_A(z) dans un espace plat avec Ω_Λ>0).

le diamètre (ou rayon ?) des BAO fonction de z n'est pas linéaire avec la distance_diametre_agulaire(z), même dans un espace euclidien ou quasi-euclidien ?

Si, puisque R_s(z)= θ_s D_A(z) avec θ_s constant.
Mais l'angle apparent (dans l'image d'un télescope) correspondant à ce diamètre varie en fonction de z.

[Lansberg]

3) Question similaire pour le CMB : le pic doppler dand le spectre de puissance angulaire est à peu près situé au multipôle l ~200 , ce qui fait ~ 1 degré : Mais là aussi, est-ce cet angle correspond au ratio entre le diamètre (ou rayon là aussi c'est pas clair ?) de l'horizon sonore (pas besoin de préciser BAO ?) qui valait à l'époque 100 h^-1 kpc et le diamètre de l'Univers à z = 1100 (soit 40 M a.l) :

un calcul très simple donne : theta = (0.1*3.26)/ 40*180/pi ~ 0.46 degrès

Comme vous le voyez, il me manque un facteur 2 pour arriver à la valeur de 1° correspondant au pic doppler.

Si quelqu'un pouvait me dire ce qui ne va pas dans ce petit calcul

Les baryons forment un pic de densité à 150 Mpc de la densité initiale de matière noire. C'est un rayon, r(s).

On a ∆théta(z) = r(s) / (1+z) Da(z)

Pour r(s) = 144,7 Mpc (mission Planck) et (1+z) Da(z) = 45,3 Gal ~13900 Mpc on a ∆théta(z) = 1,041^-2 soit ~0,6°
L'échelle angulaire du premier pic BAO est donc bien de l'ordre de 1°.

[fabio123]

Bonjour à tous, un remerciement d'abord pour toutes vos interventions, je vais y arriver, faut juste attendre que ça monte au cerveau comme dit l'autre ...

Non. Cela correspond à la distance propre des régions de l'espace qui sont à l'origine du CMB observé aujourd'hui.

Je ne comprends pas vraiment ce que tu veux dire par là :

1) tu fais référence à la taille des grumeaux du CMB qui, statistiquement, ont une taille privilégiée de 150 Mpc / 1100 ~150 kpc ? OU de 44 G a.l / 1100 = 44 M a.l (désolé je m'y paume un peu mais quel est alors la taille de l'Univers à l'époque z = 1100 ?)

OU

2) tu fais référence au rayon global qu'avait l'Univers à z = 1100, c'est-à-dire l'horizon cosmologique Dc (~44G a.l) divisé par (1+z), ce qui donne la distance diamètre angulaire à z = 1100 (pas la distance transverse mais la distance diamètre angulaire que l'on qualifie de radiale).

D'ailleurs, quelle représentation pourrait-on se faire de cette distance diamètre angulaire à z = 1100 ? peut-être que c'est la distance à laquelle se situerait à l'époque un observateur virtuel tel qu'il ne reçoit qu'aujourd'hui les photons émis à z = 1100, c'est-à dire que la lumière a mis ~ 13.7 M.a pour l'atteindre. Si c'est le cas, l'observateur se situait alors à l'époque de cette première émission à une distance de Dc/1100 ?

3) J'ai "entre parenthèse" une idée qui me vient : la distance diamètre angulaire est-elle systématiquement toujours égale à la distance transverse pour un redshift z donné. A priori oui puisque l'Univers est "presque" ou "quasi" homogène. Je veux dire par là que ce qui est valable pour le radial (distance diamètre angulaire) est aussi valable pour l'angulaire (distance transverse).

4) Réponse de yves95210 :

Si, puisque Rs(z)= θs DA(z) avec θs constant.
Mais l'angle apparent (dans l'image d'un télescope) correspondant à ce diamètre varie en fonction de z.

Je ne te cache pas que c'est assez troublant pour moi : un angle theta(s) qui est constant et qui est n'est pas constant dans le télescope : tu pourrais approfondir s'il te plaît ? pour moi, par définition,
l'angle dans un télescope est égale à tan(theta) ~ theta = Rs(z=z_emission) / (distance_qui_me_separe_de_obj et(z=z_emission) :

5)

Les baryons forment un pic de densité à 150 Mpc de la densité initiale de matière noire. C'est un rayon, r(s).

On a ∆théta(z) = r(s) / (1+z) Da(z)

Pour r(s) = 144,7 Mpc (mission Planck) et (1+z) Da(z) = 45,3 Gal ~13900 Mpc on a ∆théta(z) = 1,041^-2 soit ~0,6°
L'échelle angulaire du premier pic BAO est donc bien de l'ordre de 1°.

Quand tu parles de baryons formant un pic de densité à 150 Mpc, la valeur de 150 Mpc est bien la taille comobile des BAO, je veux dire leur diamètre, non celle à l'époque de la recombinaison, on est d'accord ?

6) Quand tu dis que "Les baryons forment un pic de densité à 150 Mpc de la densité initiale de matière noire. C'est un rayon, r(s).", es-tu sûr que ce n'est pas plutôt un diamètre, c'est-à-dire la taille totale (diamètre horizontal et vertical égaux si ça forme idéalement une sphère) ?

Dans mon calcul : 0.1*3.26/44 *180/pi, qui est légèrement à modifier à cause du h^-1, c'est-à-dire en prenant : 0.15*3.26/44 * 180/pi =0.63° :

Faut-il que je multiplie cette valeur de 0.63° par 2 pour être dans l'ordre de grandeur du pic Doppler qui est environ à 1° OU ALORS dois-je considérer le 0.15 Mpc (taille des BAO à z =1100) comme un diamètre et non un rayon ? Ce facteur 2 me semble nécessaire mais c'est juste une histoire de convention entre l'angle par rapport à la ligne de visée, auquel cas je dois considérer les 0.15 Mpc comme un rayon ou alors l'angle total qui est égale à 2 fois cet angle par rapport à la ligne de visée et ainsi considérer un diamètre au lieu d'un rayon ?

Cordialement et excusez-moi si je dis des bêtises, on apprend aussi de ses erreurs.

[Lansberg]

Je ne comprends pas vraiment ce que tu veux dire par là :

1) tu fais référence à la taille des grumeaux du CMB qui, statistiquement, ont une taille privilégiée de 150 Mpc / 1100 ~150 kpc ? OU de 44 G a.l / 1100 = 44 M a.l (désolé je m'y paume un peu mais quel est alors la taille de l'Univers à l'époque z = 1100 ?)

OU

2) tu fais référence au rayon global qu'avait l'Univers à z = 1100, c'est-à-dire l'horizon cosmologique Dc (~44G a.l) divisé par (1+z), ce qui donne la distance diamètre angulaire à z = 1100 (pas la distance transverse mais la distance diamètre angulaire que l'on qualifie de radiale).

D'ailleurs, quelle représentation pourrait-on se faire de cette distance diamètre angulaire à z = 1100 ? peut-être que c'est la distance à laquelle se situerait à l'époque un observateur virtuel tel qu'il ne reçoit qu'aujourd'hui les photons émis à z = 1100, c'est-à dire que la lumière a mis ~ 13.7 M.a pour l'atteindre. Si c'est le cas, l'observateur se situait alors à l'époque de cette première émission à une distance de Dc/1100 ?

Reprenons : ce que nous voyons sous forme du CMB "aujourd'hui" correspond à des régions qui se trouvaient à environ 41-42 Mal à l'émission de la lumière. Cela correspond à un âge cosmique de l'ordre de 380 000 ans. Mais à cette même époque ( qui est celle du découplage) la limite de l'univers observable n'était pas à 42 Mal mais beaucoup plus loin (800 ou 900 Mal, de mémoire, si je me réfère à un tableau récent fourni dans un autre fil de discussion par Gilgamesh).
À partir des données de Planck, obtenues de l'étude du CMB, on détermine la dimension angulaire Rs des BAO, figée à l'époque du découplage. On trouve Rs ~131 kpc ( x par 1100 par l'expansion).

3) J'ai "entre parenthèse" une idée qui me vient : la distance diamètre angulaire est-elle systématiquement toujours égale à la distance transverse pour un redshift z donné. A priori oui puisque l'Univers est "presque" ou "quasi" homogène. Je veux dire par là que ce qui est valable pour le radial (distance diamètre angulaire) est aussi valable pour l'angulaire (distance transverse).

Oui en théorie. Qu'il faut corriger des interactions gravitationnelles entre les amas de galaxies.

Quand tu parles de baryons formant un pic de densité à 150 Mpc, la valeur de 150 Mpc est bien la taille comobile des BAO.....je veux dire leur diamètre

Ce sont 150 Mpc à partir de la "perturbation centrale", comme l'onde formée par un caillou tombant dans l'eau. C'est un rayon.

6) Quand tu dis que "Les baryons forment un pic de densité à 150 Mpc de la densité initiale de matière noire. C'est un rayon, r(s)."

Oui. Réponse précédente.

Faut-il que je multiplie cette valeur de 0.63° par 2 pour être dans l'ordre de grandeur du pic Doppler qui est environ à 1°

Oui. ∆théta(s) est de 0,01041 rad pour Rs (donnée Planck). Pour une Da ~42 Mal on trouve bien Rs = 0,01041 x 41 x 10^6 ~427 000 a.l = 131 kpc
Et pour l'époque actuelle : Rs = 0,01041 x 45,3 x 10^9 /3261,6 ~144,6 Mpc

[fabio123]

Bonjour Lansberg,

ce que nous voyons sous forme du CMB "aujourd'hui" correspond à des régions qui se trouvaient à environ 41-42 Mal à l'émission de la lumière

Si je te comprends, j'en déduis qu'à 380.000 ans, l'univers n'était pas complètement rempli d'un plasma baryons-photons sur le point de se découpler, je veux dire que la zone au delà de 41-42 Mal était "vide" ? Mais j'ai du mal à me dire qu'il y avait une grosse bulle de plasma baryons-photons jusqu'à 41-42 Mal et après plus rien : c'est en fait la non-coïncidence entre la taille physique de l'Univers et la Distance diamètre angulaire à z = 1100, qui me trouble.

la limite de l'univers observable n'était pas à 42 Mal mais beaucoup plus loin (800 ou 900 Mal, de mémoire, si je me réfère à un tableau récent fourni dans un autre fil de discussion par Gilgamesh).
À partir des données de Planck, obtenues de l'étude du CMB, on détermine la dimension angulaire Rs des BAO, figée à l'époque du découplage.

Je serais bien curieux de pouvoir déterminer la taille de l'Univers au moment du découplage : je n'ai pas trouvé le tableau de Gilgamesh dont tu parles : pourrais-tu s'il te plaît m'envoyer un lien vers ce tableau ou une formule simple pour arriver à une taille de 800 ou 900 M a.l ?

L'angle de 1 ° du pic doppler correspond t-il au rayon ou diamètre des BAO ? (si c'était uniquement le rayon d'une onde comme tu dis, on s'attendrait plutôt à une valeur de 0.6° et non le double ~ 1*).

Cordialement

[Lansberg]

Si je te comprends, j'en déduis qu'à 380.000 ans, l'univers n'était pas complètement rempli d'un plasma baryons-photons sur le point de se découpler, je veux dire que la zone au delà de 41-42 Mal était "vide" ?

Mais j'ai du mal à me dire qu'il y avait une grosse bulle de plasma baryons-photons jusqu'à 41-42 Mal et après plus rien : c'est en fait la non-coïncidence entre la taille physique de l'Univers et la Distance diamètre angulaire à z = 1100, qui me trouble.

Bien sûr que l'univers, dans son ensemble, était constitué d'un plasma baryons/photons/matière noire.
Il y a juste à comprendre que les régions que nous voyons sous forme du CMB étaient situées à ~ 42 Mal autour de notre propre région de l'espace. Cela ne constitue en aucun cas un quelconque horizon à l'époque du découplage. Ces régions nous fuyaient avec une vitesse de récession considérable (de l'ordre de 50.c je crois). La limite de la sphère de Hubble était de l'ordre de 600 000 a.l (distance à partir de laquelle la vitesse de récession est égale à c).

Je serais bien curieux de pouvoir déterminer la taille de l'Univers au moment du découplage : je n'ai pas trouvé le tableau de Gilgamesh dont tu parles : pourrais-tu s'il te plaît m'envoyer un lien vers ce tableau ou une formule simple pour arriver à une taille de 800 ou 900 M a.l ?

Tu trouveras le tableau en question dans ce fil : https://forums.futura-sciences.com/q...edshift-z.html


La formule de calcul n'est pas simple. Elle tient compte des différents omégas (en espace plat ΩK=0) et nécessite d'intégrer entre 0 et le facteur d'échelle désiré (la borne sup pour ce qui t'intéresse vaut 1/1100 qui est le facteur d'échelle au découplage).

L'angle de 1 ° du pic doppler correspond t-il au rayon ou diamètre des BAO ? (si c'était uniquement le rayon d'une onde comme tu dis, on s'attendrait plutôt à une valeur de 0.6° et non le double ~ 1*).

∆Théta(s) = 0,01041 rad = 0,6° correspondant à Rs (rayon). C'est bien ce que j'écris dans mon précédent message, non ?

[fabio123]

Bonjour,

1) j'ai voulu calculer la taille de l'Univers observable avec une résolution numérique. Voici le résultat sur cette figure ci-dessous :

Pièce jointe 422481

Pour cela j'ai intégré entre z = 1100 et z = 10^6. Je ne vois pour l'instant une justification de prendre la borne inférieure à z=0 car je m'intéresse à l'époque de la recombinaison, pas celle d'aujourd'hui mais si c'est faux, toute justification est la bienvenue.

2) Après, autre remarque, je vois, si ces résultats sont valides, que la taille de l'Univers observable reste constant à partir de z = 10^6 (autour des 800 Mal) : est-ce normal ?

3) De plus, la courbe LCDM est preque confondue (rouge) avec celle d'un modèle sphérique (noire) (dont la somme des Omega est aussi proche de 1) : les univers plats seraient alors proches des univers de type sphérique ? (tant qu'on a une somme des Omega proche de 1 ?)

4)

Il y a juste à comprendre que les régions que nous voyons sous forme du CMB étaient situées à ~ 42 Mal autour de notre propre région de l'espace

ce n'est toujours pas clair dans ma tête. Si l'Univers observable était d'environ 800 Mal, cela fait à peine une vingtaine de "régions que nous voyons sous forme de CMB", ce qui me semble assez peu, tu ne penses pas qu'il y a un soucis ?

5) Mon problème est d'avoir du mal à imaginer un observateur comobile situé dans le plasma de baryons/photon/matière noire et de me dire : "il y a une région du CMB qui se situe à 42 Mal de moi", ça ne me paraît pas logique puisque je suppose que cet observateur comobile est déjà dans le plasma, qui est de taille 800 Mal, et qui est sur le point de se découpler : "une région du CMB" est-elle une fluctuation de BAO ou un ensemble de fluctuations BAO ou l'ensemble du CMB ? tu comprends cette subtilité que je ne saisis pas ?

6) Si le rayon de l'Univers observable est constant pour z> 10^6, Alors le scénario du modèle de l'inflation serait quelque part privilégié car ça expliquerait que des région à priori non causales d'avoir la même température.

Merci pour votre aide.

[Lansberg]

Bonjour,

1) j'ai voulu calculer la taille de l'Univers observable avec une résolution numérique. Voici le résultat sur cette figure ci-dessous :

Pour cela j'ai intégré entre z = 1100 et z = 10^6. Je ne vois pour l'instant une justification de prendre la borne inférieure à z=0 car je m'intéresse à l'époque de la recombinaison, pas celle d'aujourd'hui mais si c'est faux, toute justification est la bienvenue.

Je n'ai pas dit de prendre z=0. C'est le facteur d'échelle qui vaut a=0 pour la borne inférieure et a=1/1100 pour la borne supérieure (découplage). Cela donne la distance de l'horizon des particules pour a=1/1100.

2) Après, autre remarque, je vois, si ces résultats sont valides, que la taille de l'Univers observable reste constant à partir de z = 10^6 (autour des 800 Mal) : est-ce normal ?

Si z tend vers ∞ alors "a" tend vers 0, ce qui correspond à ma réponse précédente. Les 800 Mal sont cohérents avec ce qui est attendu pour z=1100.

ce n'est toujours pas clair dans ma tête. Si l'Univers observable était d'environ 800 Mal, cela fait à peine une vingtaine de "régions que nous voyons sous forme de CMB", ce qui me semble assez peu, tu ne penses pas qu'il y a un soucis ?

Je ne comprends pas ! C'est quoi cette histoire de 20 régions ? (800/42 ???). Ça n'a pas de sens.

5) Mon problème est d'avoir du mal à imaginer un observateur comobile situé dans le plasma de baryons/photon/matière noire et de me dire : "il y a une région du CMB qui se situe à 42 Mal de moi", ça ne me paraît pas logique puisque je suppose que cet observateur comobile est déjà dans le plasma, qui est de taille 800 Mal, et qui est sur le point de se découpler : "une région du CMB" est-elle une fluctuation de BAO ou un ensemble de fluctuations BAO ou l'ensemble du CMB ? tu comprends cette subtilité que je ne saisis pas ?

Pour n'importe quel observateur présent dans l'univers à l'époque du découplage, les régions de l'espace situées sur une sphère centrée sur lui à 42 Mal, et qui ne sont qu'un plasma de matière/rayonnement, sont vues par les observateurs "actuels" sous forme du CMB. C'est valable pour n'importe quel observateur dans l'univers (observable et au-delà à priori). Le terme "régions" n'a rien à voir ici avec les BAO.
L'horizon des particules pour tout "observateur" à l'époque du découplage est à 800 Mal. Cela ne veut pas dire que la taille de l'univers est de 800 Mal. Il est peut-être infini.

6) Si le rayon de l'Univers observable est constant pour z> 10^6, Alors le scénario du modèle de l'inflation serait quelque part privilégié car ça expliquerait que des région à priori non causales d'avoir la même température.

Pour z>10^6, "a" continue à tendre vers zéro et H à tendre vers l'infini. Le rayon de l'univers observable n'est pas constant (voir tableau de Gilgamesh) au moins en remontant jusqu'à l'inflation. Cette dernière (entre 10^-38 s et 10^-36 s) permet en effet d'expliquer que des régions de l'espace qui ne sont pas à priori reliées causalement aujourd'hui, l' étaient en fait avant l'inflation d'où des températures semblables.

[Gilgamesh]

Bonjour,

1) j'ai voulu calculer la taille de l'Univers observable avec une résolution numérique. Voici le résultat sur cette figure ci-dessous :

Pièce jointe 422481
.

la PJ n'est pas valide. Peut être une question de format ?
Pour le reposter faut que tu fasses Aller en mode avancé / Gérer les pièces jointes et poster une image (gif, jpeg ou png) ou un pdf

[Gilgamesh]

5) Mon problème est d'avoir du mal à imaginer un observateur comobile situé dans le plasma de baryons/photon/matière noire et de me dire : "il y a une région du CMB qui se situe à 42 Mal de moi", ça ne me paraît pas logique puisque je suppose que cet observateur comobile est déjà dans le plasma, qui est de taille 800 Mal, et qui est sur le point de se découpler : "une région du CMB" est-elle une fluctuation de BAO ou un ensemble de fluctuations BAO ou l'ensemble du CMB ? tu comprends cette subtilité que je ne saisis pas ?

Pose toi sur une feuille quadrillé et fait un schéma en prenant des valeurs dans l'abaque.

Par exemple pour a=0,00004
l'âge est d'environ 2000 ans. L'horizon fait 59 Mly (18,1 Mpc). Le taux d'expansion est de 280 million de km/s/Mpc. Je multiplie les deux : 280 million km/s/Mpc * 18,1 Mpc et j'obtiens une vitesse de 17 c. Comme expliqué par Landberg ce n'est pas parce que tu vois la région au temps t cosmique (le même pour tous les observateurs comobiles) qu'en ce moment même il n'est pas en train de s'éloigner plus vite que c. Si je divise la distance à l'horizon à cet âge la par le facteur d'échelle pour savoir à quelle distance de nous se trouve cette région aujourd'hui, j'obtient 1470 Gly : bien plus loin que l'horizon actuel. Cela signifie que les régions qui formaient l'horizon de cette époque ont depuis longtemps passé derrière l'horizon cosmologique (et qu'elle n'y rentreront plus jamais --sauf si l'expansion s'arrête un jour bien sûr)