Redshift - dualité variable temporelle et spatiale - Calcul des BAO

[fabio123]

Bonjour,

dans un contexte de calculs sur la taille des BAO (Oscillations acoustiques des baryons), je voulais avoir une précision sur la notion de redshift.

Dans le livre "initiation à la cosmologie" de Marc Lachièze-Rey, celui-ci évoque la dualité de ce que représente le redshift. A la fois, il peut représenter
une époque donné comme pour le calcul du temps cosmique ou le temps de "regard en arrière" (lookback time) qui permet de savoir pendant combien de
temps la lumière d'un objet s'est propagé avant de nous atteindre.

Par exemple, le calcul du "temps de regard en arrière" se calcule ainsi (dans le cadre de la métrique FLRW) :



On voit bien que pour un donné, on a une valeur du temps (qualifié de "cosmique" si on intègre depuis z=0 ?).

Maintenant, on aussi la formule suivante (toujours dans le cadre FLRW) qui permet de calculer la coordonnée comobile d'un objet à un redshift situé à :



J'ai l'impression que ces 2 exemples montrent assez bien le double aspect derrière la variable "redshift" (une époque donc temporelle mais aussi une distance associée à elle).

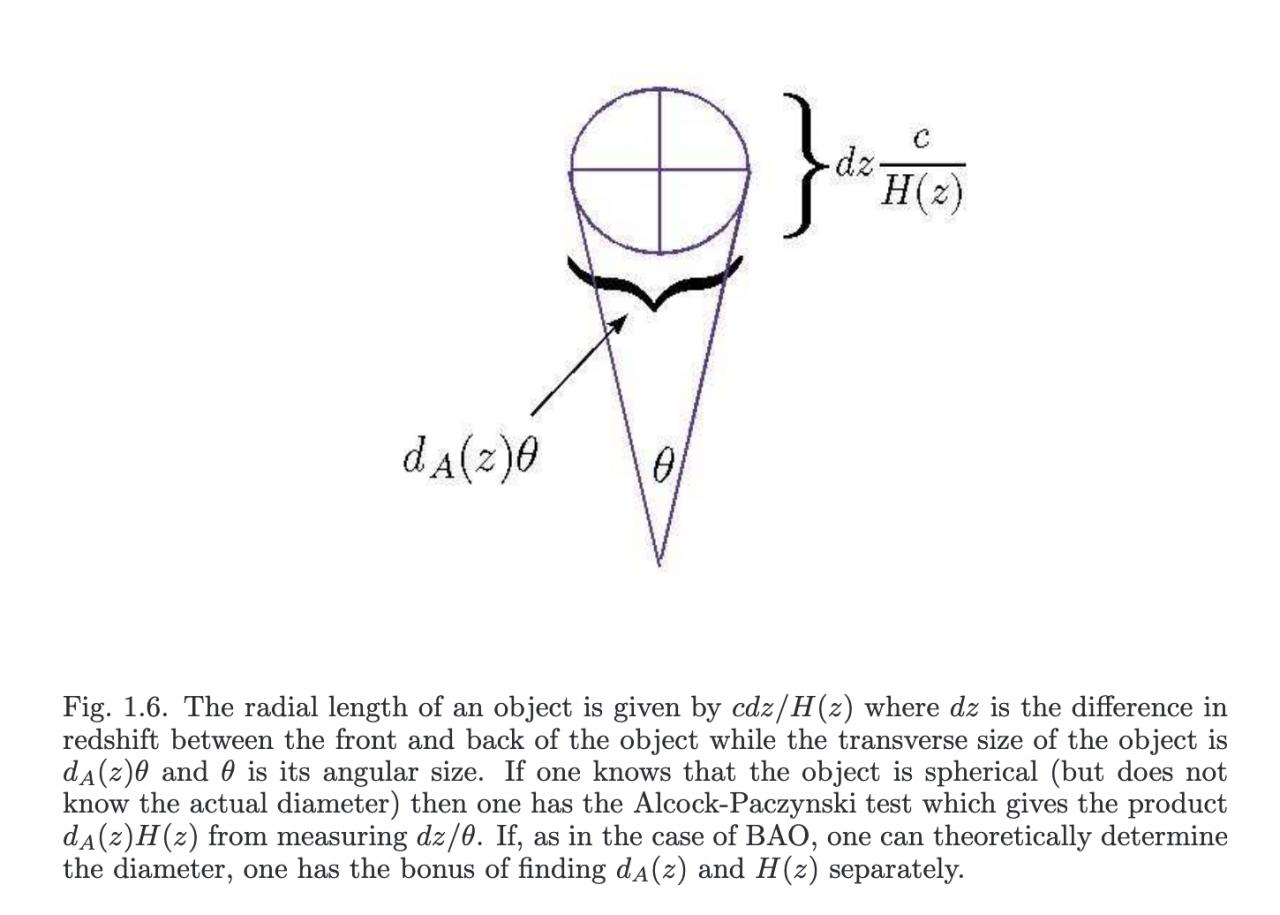
Mais là où ça ne va pas pour moi, c'est dans le calcul de la taille des BAO. Voici une figure qui illustre mon problème :



En effet, on voit que pour la composante radiale, je veux dire la composante en redshift "z", si je suis mon raisonnement ci-dessus, je ne comprends pas à quoi correspond le dans l'expression . Je me dis que ce Delta correspond à 2 époques différentes et en même temps, je me dis que ce qui compte, c'est le calcul de la composante radiale, c'est-à-dire le calcul du , c'est-à-dire la taille physique en profondeur (radiale) des BAO.

Je bloque en me disant : dans ce , j'ai le bord externe, je veux dire le plus éloigné correspondant à et le bord le plus proche de nous correspondant à , mais si je suis le raisonnement de la dualité "temps/distance", je pourrais en conclure que la taille n'est pas calculé à un seul et même instant : quand on mesure une distance au sens classique, on suppose qu'on a accès instantanément aux 2 extrémités de l'objet à mesurer.

Or ici, je fais des confusions sur cette notion de simultanéité dans la mesure de la taille du BAO, qui pour moi, doit être mesurée à une époque donnée de l'Univers, donc à un seul et même instant, ce qui n'est pas le cas si je considère un ( correspond à une époque plus éloigné dans le passé que ). Je comprends bien que le résultat final sera une distance mais cette question de delta en redshift dans l'intégrale pour ce calcul me perturbe.

Par contre, pour la composante transverse, c'est beaucoup plus facile d'imaginer un calcul simultané de distance (ici transverse) car cette composante a ses 2 bords qui sont à la même distance que nous, il n'y a qu'un seul redshift considéré, donc une seule et même époque donnée par un seul redshift.

Si quelqu'un pouvait m'expliquer l'origine de ma confusion pour la composante radiale, ça serait sympa... cette dualité, si elle est bien réaliste, m'embrouille + qu'autre chose dans cet exemple.

Merci, Bonne journée !

ps : n'hésitez pas à me demander des infos supplémentaires au cas où j'aurais mal formulé ma question.
-----

[Lansberg]

Bonjour,

pour pouvoir répondre il faudrait d'abord relire la question en ajoutant tous les mots qui manquent !!

[Gilgamesh]

Mais pour ce que j'ai ai compris, vu que l'objet a une certaine extension le bord interne sera observé à un z légèrement différent du bord externe et tu peux faire la différence des deux pour avoir la taille

[fabio123]

@Lansberg [mots] il en manque tant que ça des mots ?

Ma question n'est pas compréhensible ?

Merci de me dire là où j'ai fauté

[A voir en vidéo sur Futura]

[fabio123]

oui mais du coup, si les 2 redshifts sont différents, ils correspondent à 2 époques différentes, n'est-ce pas ? c'est ça qui me pose problème, quand on mesure, sur Terre, on suppose voir les 2 extrémités au même moment.

Toujours le même souci, j'associe un redshift donné à une époque donnée.

[Lansberg]

@Lansberg [mots] il en manque tant que ça des mots ?

Ma question n'est pas compréhensible ?

Merci de me dire là où j'ai fauté

J'ai mis des ???? là où manquent les mots. Même si parfois on devine, ça ne le fait pas !!

"Par exemple, le calcul du "temps de regard en arrière" se calcule ainsi (dans le cadre de la métrique FLRW) : ????

On voit bien que pour un ???? donné.

Maintenant, on aussi la formule suivante (toujours dans le cadre FLRW) qui permet de calculer la coordonnée comobile d'un objet à un redshift situé à : ?????

...je ne comprends pas à quoi correspond le ????? dans l'expression .

Je bloque en me disant : dans ce ???? , j'ai le bord externe,

...c'est-à-dire le calcul du ????? , c'est-à-dire la taille physique...

ce qui n'est pas le cas si je considère un ????? ( correspond à une époque plus éloigné dans le passé que )."

[fabio123]

Non mais ce ne sont pas des mots qui manquent mais carrément les équations Latex.

Tu veux dire que tu as une série de points d'interrogation à la place des équations ?

Bizarre, pourtant chez moi, les équations apparaissent bien.

Il faudrait qu'une autre personne puisse faire le test en disant s'il voit bien ou pas les équations Latex.

Pourtant, j'ai bien utilisé les balises [ TEX ] et [ /TEX ]. (ici sans espace entre les crochets pour TEX et pas en italique)

Je sais par expérience que la gestion des équations déconne parfois sur les forums Futura.

Si c'est une utilisation mauvaise de ma part, je m'en excuse car sans équations, il est sûr que tu ne vas pas comprendre la problématique.

[fabio123]

Pour être plus précise, j'ajoute à ma première phrase de la réponse précédente :

Non mais ce ne sont pas des mots qui manquent mais carrément les symboles et équations Latex.

[fabio123]

ainsi que :

Pourtant, j'ai bien utilisé les balises [ TEX ] et [ /TEX ]. (ici sans espace entre les crochets pour TEX et pas en italique)

[yves95210]

Non mais ce ne sont pas des mots qui manquent mais carrément les équations Latex.

Tu veux dire que tu as une série de points d'interrogation à la place des équations ?

Bizarre, pourtant chez moi, les équations apparaissent bien.

Il faudrait qu'une autre personne puisse faire le test en disant s'il voit bien ou pas les équations Latex.

Salut,

je vois bien les équations (déjà hier, la première fois que j'ai lu ton message). Mais c'est vrai que la gestion du TeX par le forum est quelque peu surprenante, j'ai déjà eu le même genre de problème.
mach3 m'avait conseillé d'ajouter des espaces dans les expressions pour aider l'interpréteur TeX du forum à s'y retrouver... Je ne sais plus après quels symboles en particulier, mais par défaut du peux en ajouter partout où ça ne change pas le sens de l'expression TeX. C'est un peu fastidieux mais ça marche.

[yves95210]

oui mais du coup, si les 2 redshifts sont différents, ils correspondent à 2 époques différentes, n'est-ce pas ? c'est ça qui me pose problème, quand on mesure, sur Terre, on suppose voir les 2 extrémités au même moment.

Toujours le même souci, j'associe un redshift donné à une époque donnée.

Il suffit de raisonner en distances radiales (et transverses) comobiles, non ?
Dans ce cas la différence entre les distances de tes 2 extrémités est la distance que tu mesurerais à l'époque actuelle, i.e. sur l'hypersurface spatiale à t₀=aujourd'hui, si c'était physiquement possible d'effectuer une telle mesure. Et cela vaut aussi bien pour la distance transverse que pour la distance radiale.

Si tu ne l'as pas déjà fait, jette un coup d’œil à ce papier, dont j'extrais la citation ci-dessous :

In some sense the line-of-sight comoving distance is the fundamental distance measure in cosmography since, as will be seen below, all others are quite simply derived in terms of it. The line-of-sight comoving distance between two nearby events (ie, close in redshift or distance) is the distance which we would measure locally between the events today if those two points were locked into the Hubble flow. It is the correct distance measure for measuring aspects of large-scale structure imprinted on the Hubble flow, eg, distances between “walls.”

[Lansberg]

Non mais ce ne sont pas des mots qui manquent mais carrément les équations Latex.

Tu veux dire que tu as une série de points d'interrogation à la place des équations ?

Il n'y a rien du tout. Juste un espace à la place des équations. J'ai mis des ???? pour marquer les emplacements.
Habituellement il n'y a pas de problème avec Latex.

[yves95210]

Il n'y a rien du tout. Juste un espace à la place des équations. J'ai mis des ???? pour marquer les emplacements.
Habituellement il n'y a pas de problème avec Latex.

Si, il y en a parfois. J'y ai été confronté à plusieurs reprises. Et comme je l'ai dit tout à l'heure, j'avais pu lire correctement le message de Fabio hier, avant que tu y répondes en mentionnant qu'il y manquait des mots (en fait, les équations).
J'ai l'impression que les expression TeX sont ré-interprétées par l'outil de gestion du forum à chaque fois que le message les contenant est affiché par un utilisateur (il vaudrait sans-doute mieux que ce soit fait une fois pour toutes lorsque le message est enregistré, non ?), et que l'interpréteur bégaie parfois, conduisant à des affichages différents pour différents utilisateurs - ce qui fait que la personne qui a posté le message ne peut pas savoir qu'il sera mal lu par d'autres.

[yves95210]

PS
@Lansberg : j'ai recopié ci-dessous la première équation du message de Fabio, en ajoutant des espaces avant les symboles TEX. Est-ce qu'elle s'affiche correctement chez toi ?

[Lansberg]

Salut yves..

Toujours rien. Avec aucun navigateur.

[Gilgamesh]

oui mais du coup, si les 2 redshifts sont différents, ils correspondent à 2 époques différentes, n'est-ce pas ? c'est ça qui me pose problème, quand on mesure, sur Terre, on suppose voir les 2 extrémités au même moment.

Toujours le même souci, j'associe un redshift donné à une époque donnée.

Depuis 1905 ça n'existe plus en physique la possibilité de voir un objet étendu "au même moment". Tu vois ton nez plus jeune que tes pieds. Et si tu as une horloge atomique au bout de ton nez et une autre sur l'orteil, la fraction de ns de différence entre ce qu'affichent les deux horloges va te donner la distance qui les sépare. Ici, l'âge est mesuré par le z.

[Lansberg]

PS
@Lansberg : j'ai recopié ci-dessous la première équation du message de Fabio, en ajoutant des espaces avant les symboles TEX. Est-ce qu'elle s'affiche correctement chez toi ?

Visiblement, il y a des soucis avec LaTex : https://forums.futura-sciences.com/n...80513-tex.html

[yves95210]

Visiblement, il y a des soucis avec LaTex : https://forums.futura-sciences.com/n...80513-tex.html

Oui, c'est récurrent...

Au passage, la "recette de cuisine" consistant à ajouter des espaces avant les symboles LaTeX est hors-sujet dans le cas présent. Elle ne répond qu'au cas où l'équation s'affiche, mais avec des bouts mal interprétés, un symbole ayant été vu par l'interpréteur comme faisant partie de la chaîne de caractères qui le précède (Si, si , ça arrive).
Alors que là, elle ne s'affiche carrément pas (du moins chez toi ).

[Mailou75]

Salut Fabio,

Pour moi, la figure que tu donnes ne fonctionne que pour des objets ayant une profondeur visuellement. Dans ce cas effectivement l'avant et l'arrière correspondent à des époques et donc des H(z) différents donc la formule est fausse puisqu'elle ne donne qu'un seul H(z). Soit tu négliges la profondeur et dans ce cas dz=0 la formule est juste mais inutile, soit elle est fausse...

En fait pour les BAO, on observe le CMB, donc une coque (surface d'émission), un objet qui n'a pas de profondeur. Donc la formule avec dz, quoi qu'il arrive ne sert à rien. Par contre la formule tan(O)=rayon du cercle vu/distance angulaire (ici approximée par tan(O)~O) est juste. On suppose connaitre la taille d'une "vague" dans le plasma originel et on suppose connaitre le z=température de découplage/température actuelle=3000K/2,7K~1100. Dans ce cas on retrouve que la distance angulaire (dA) donnée par les équations que tu donnes (et qui apparaissent très bien) vérifie le rapport diamètre vu = dA*O. C'est une validation du modèle en vogue, mais comme tu l'auras compris cela demande quelques suppositions sur nos connaissances...

En espérant avoir aidé...

[Gilgamesh]

Salut Fabio,

Pour moi, la figure que tu donnes ne fonctionne que pour des objets ayant une profondeur visuellement. Dans ce cas effectivement l'avant et l'arrière correspondent à des époques et donc des H(z) différents donc la formule est fausse puisqu'elle ne donne qu'un seul H(z). Soit tu négliges la profondeur et dans ce cas dz=0 la formule est juste mais inutile, soit elle est fausse...

En fait pour les BAO, on observe le CMB, donc une coque (surface d'émission), un objet qui n'a pas de profondeur. Donc la formule avec dz, quoi qu'il arrive ne sert à rien. Par contre la formule tan(O)=rayon du cercle vu/distance angulaire (ici approximée par tan(O)~O) est juste. On suppose connaitre la taille d'une "vague" dans le plasma originel et on suppose connaitre le z=température de découplage/température actuelle=3000K/2,7K~1100. Dans ce cas on retrouve que la distance angulaire (dA) donnée par les équations que tu donnes (et qui apparaissent très bien) vérifie le rapport diamètre vu = dA*O. C'est une validation du modèle en vogue, mais comme tu l'auras compris cela demande quelques suppositions sur nos connaissances...

En espérant avoir aidé...

Le CMB n'est pas strictement plat, le phénomène n'est pas instantanée et l'épaisseur de la surface de dernière diffusion a un Δz ~ 80 (quand même !) ce qui correspond à une durée de 110 ka environ.

Mais pour la question de Fabio je pense que ça concerne l'observation des BAO dans l'univers proche (fonction de corrélation à 2 point sur le Sloan Digital Sky Survey). Fabio tu confirme ?

[yves95210]

Pour moi, la figure que tu donnes ne fonctionne que pour des objets ayant une profondeur visuellement. (...)

En fait pour les BAO, on observe le CMB, donc une coque (surface d'émission), un objet qui n'a pas de profondeur.

La question de Fabio concerne plutôt la détermination du diamètre des BAO à partir de l'observation des galaxies dans l'univers récent, grâce à la surabondance de galaxies séparées par une distance correspondant (par application du modèle cosmologique standard) au "sound horizon" de l'univers primordial.
Le rapport entre cette distance et le sound horizon déduit des observations du CMB donne une contrainte sur la valeur des paramètres de ce modèle.

PS : désolé pour le croisement avec Gilgamesh.

[Mailou75]

Le CMB n'est pas strictement plat, le phénomène n'est pas instantanée et l'épaisseur de la surface de dernière diffusion a un Δz ~ 80 (quand même !) ce qui correspond à une durée de 110 ka environ.

Soit, mais qui dit Δz dit ΔH(z) ce qui n'apparait pas dans la formule. Pour moi elle reste fausse... d'approximation en approximation on pourrait arriver à dire n'importe quoi. La cosmo c'est "open" mais quand même...

[fabio123]

Bonjour,

Merci à tous pour vos réponses, malgré les tribulations d'affichage Latex. En fait, je me rends compte que ma figure peut prêter à confusion, c'est-à-dire qu'il montre une profondeur mais on ne sait pas si c'est une
profondeur en distance ou en redshift. Je pense que ma confusion vient de là. Pour la composante transverse, on est tous d'accord que la formule et le principe sont justes, on a déjà vu ça.

Après, pour la composante parallèle, je crois qu'il faut raisonner en termes de distance comobile, comme dit yves95210. Pour calculer la distance comobile du bord exterme, j'ai besoin d'intégrer sur z la formule
(c / H(z)), ça me donnera la distance comobile, je veux celle de maintenant, i.e à un redshift actuel z=0.

C'est ce (\Delta z) qui m'embrouille si ce que je viens d'expliquer est correct (avec \Delta z = z_2 -z_1 qui
correspond à 2 époques différentes).

Sinon, concernant la réponse de Gilgamesh :

Depuis 1905 ça n'existe plus en physique la possibilité de voir un objet étendu "au même moment". Tu vois ton nez plus jeune que tes pieds. Et si tu as une horloge atomique au bout de ton nez et une autre sur l'orteil, la fraction de ns de différence entre ce qu'affichent les deux horloges va te donner la distance qui les sépare. Ici, l'âge est mesuré par le z.

On peut très bien imaginer un observateur comobile avec la zone d'un BAO considéré (je veux dire une distance "privilégiée considérée) qui recevrait les signaux des 2 extrémités en même temps, cet observateur se trouvant à mi chemin entre les 2 extrémités (je sais, c'est un peu tiré par les cheveux). Mais alors dans ce cas, il aurait accès à la taille sans avoir recours à ce (\Delta z) puisque qu'il serait certain que les 2 bords ont été mesuré à une même époque ?

Il me semble qu'un ami m'a parlé de "cosmic chronometer" pour ce calcul de la composante radiale, je ne sais pas si ça vous parle. Comme indiqué sur la figure, en supposant le BAO sphérique, la composante radiale et transverse étant égales, on peut avoir accès à la distance diamètre angulaire et/ou H(z) en égalant les 2 formules (on appelle ça le "Test d'Alcock-Pazinsky").

Tout ceci pour dire que mon schéma est vraiment trompeur pour la composante radiale. Je poursuis mes investigations pour mieux comprendre ce calcul faisant intervenir ce (\Delta z) contredisant ma perception intuitive de mesurer la "distance physique" dans le sens radial à une époque donnée.

ps : @Mailou : je me suis toujours demandé si l'on devait considérer, dans le langage courant astrophysique, les BAO comme une sonde proche (c'est-à-dire en calculant les fonctions de corrélations à 2 points à partir des données collectés par les surveys plus ou moins récents (disons jusqu'à z < 3-4), OU ALORS comme une sonde éloignée (primordiale) (avec le calcul de l'angle theta ~ tan(theta) = taille_BAO_au_decouplage / (Distance diamètre angulaire au moment découplage) , angle qui doit rester constant au cours du temps cosmique et qui est justement une empreinte de la taille observée aujourd'hui de la distance "privilégiée" qu'ont tendance à avoir les galaxies entre elles).

Aujourd'hui, il me semble que la distance comobile des BAO est de l'ordre de 150 Mpc, quelqu'un pourrait me le confirmer ? ça donnerait alors une taille de (150 Mpc)(1+z) ~ 0.15 Mpc pour leur distance diamètre angulaire au moment du découplage du CMB à z = 1100. Là aussi, je joue avec le feu en égalant la "taille physique d'un BAO" et la notion de distance comobile/angulaire, c'est un peu confus encore. ça suppose sûrement qu'on a une symétrie sphérique.


Vos remarques ou explications supplémentaires seront les bienvenues, et si je dis des bêtises, aussi, n'hésitez pas, on apprend de ses erreurs...

[Gilgamesh]

Bonjour,

Merci à tous pour vos réponses, malgré les tribulations d'affichage Latex. En fait, je me rends compte que ma figure peut prêter à confusion, c'est-à-dire qu'il montre une profondeur mais on ne sait pas si c'est une profondeur en distance ou en redshift.

Quelle différence fais tu entre les deux ? Pour passer du Δz au Δr y'a juste un facteur c/H. On mesure le diamètre des BAO dans la direction radiale par Δz c/H(z) et dans la dimension transverse par Δθ (1+z)Da

source : http://isapp2015.in2p3.fr/talks/Perc...lustering1.pdf (chercher à "BAO as a standard ruler")

Et la taille des BAO aujourd'hui est bien de l'ordre de 150 Mpc

[Mailou75]

Salut,

C'est ce (\Delta z) qui m'embrouille si ce que je viens d'expliquer est correct (avec \Delta z = z_2 -z_1 qui
correspond à 2 époques différentes).

Je suis comme toi, je suis perplexe, si le Δz est non négligeable alors il s'agit bien d'époques différentes.

On peut très bien imaginer un observateur comobile avec la zone d'un BAO considéré (je veux dire une distance "privilégiée considérée) qui recevrait les signaux des 2 extrémités en même temps (...)

Impossible, tu as fait le calcul toi même. Si une BAO mesurait 0,15MPc à l'émission alors c'est trop près... Aujourd'hui on voit ce qui était à 42Mal lors du découplage, soit 13MPc. On verra plus loin plus tard mais jamais plus près, les rayons sont passés depuis longtemps. Dommage

(on appelle ça le "Test d'Alcock-Pazinsky").

p52 du lien de Gilga. Rien compris... mais je peux juste te conseiller de faire attention avec les notations et formulations. Dans leur dessin, ce qui est noté D_A c'est le diamètre angulaire (transversal), alors que ce qu'on note habituellement dA c'est la distance angulaire (radial). Les deux sont en mètres locaux/actuels. Toi même à plusieurs reprises tu parles de "distance diamètre angulaire" qui est un amalgame des deux notions

Je profite de ce schéma pour un rapide aparté : Les photons ont été émis à la distance qui est vue aujourd'hui (= correspond à la taille d'un objet connu à cette distance) mais ils ont reculé (avec l'espace et relativement à l'observateur) jusqu'à ~5,7Gal puis ont fini par revenir avec la baisse du taux d'expansion. Mais ils ont fait tout ça le long de leur radiale respective et l'angle entre elles ne varie pas c'est pour ça qu'on parle de distance angulaire : ça n'a rien à voir avec ce qui se passe en espace plat (des rayons qui vont tout droit vers l'observateur) mais ça revient au même. Bref, j'ai peut être enfoncé une porte ouverte...

Tout ceci pour dire que mon schéma est vraiment trompeur pour la composante radiale. Je poursuis mes investigations pour mieux comprendre ce calcul faisant intervenir ce (\Delta z) contredisant ma perception intuitive de mesurer la "distance physique" dans le sens radial à une époque donnée.

Le schéma est trompeur dans le sens où il laisse supposer qu'une sphère vue pourrait être l'image d'une sphère réelle. Dans le bon sens ça donne : un objet comobile sphérique ne sera jamais vu comme une sphère. Aux alentours de z=1,65 une sphère sera vue complètement aplatie radialement. A des z plus élevés (centaines) une sphère (la même) sera vue plus petite et surtout étirée radialement cette fois. Bien sur c'est en considérant un Δz non négligeable.

ps : @Mailou : je me suis toujours demandé si l'on devait considérer, dans le langage courant astrophysique, les BAO comme une sonde proche (c'est-à-dire en calculant les fonctions de corrélations à 2 points à partir des données collectés par les surveys plus ou moins récents (disons jusqu'à z < 3-4), OU ALORS comme une sonde éloignée (primordiale) (avec le calcul de l'angle theta ~ tan(theta) = taille_BAO_au_decouplage / (Distance diamètre angulaire au moment découplage) , angle qui doit rester constant au cours du temps cosmique et qui est justement une empreinte de la taille observée aujourd'hui de la distance "privilégiée" qu'ont tendance à avoir les galaxies entre elles).

Pas sur de comprendre la question mais j'aurais dit réponse 2. Cela dit, au message 20 Gilga parle de "fonction de corrélation à 2 points sur le Sloan Digital Sky Survey" donc la réponse doit être : les deux mon capitaine !

.......

Pour passer du Δz au Δr y'a juste un facteur c/H. On mesure le diamètre des BAO dans la direction radiale par Δz c/H(z)

C'est quand même n'importe quoi... déjà on de fait pas varier H(z) quand z varie, alors qu'on sait qu'une petite variation de z engendre une grooosse variation de H(z). De plus, si on mesure un intervalle de distances angulaires alors il faut tenir compte de ce qui est dit plus haut : allongement radial visuel pour les z élevés. Enfin, si on mesure une onde qui serait partie dans les deux sens radialement (+expansion), l'avant et l'arrière de la sphère devraient avoir une vitesse propre engendrant un Doppler supplémentaire, l'utilisation directe du décalage z+1 parait impossible.

source : http://isapp2015.in2p3.fr/talks/Perc...lustering1.pdf (chercher à "BAO as a standard ruler")

page 49 (rien compris, notations barbares)

A+ je vous laisse entre gens sérieux, le fil n'en sera que plus lisible

Mailou

[Lansberg]

Je suis comme toi, je suis perplexe, si le Δz est non négligeable alors il s'agit bien d'époques différentes.

Non.
On parle ici de BAO et le cercle sur le premier schéma correspond à une région de surdensité provoquée par la propagation d'onde sonore dans le plasma avec une vitesse de c.√3 (onde, qu'il faut imaginer partir du centre du cercle). Au moment de la recombinaison, la surdensité est figée. Le ∆z "délimite" un phénomène qui s'est produit à la même époque (∆z ~ 0,035 pour l'univers proche). D'où la pertinence de pouvoir calculer H(z) connaissant sH (horizon sonique ~150 Mpc) et ∆z (mesure).

[Mailou75]

Salut,

On parle ici de BAO et le cercle sur le premier schéma correspond à une région de surdensité provoquée par la propagation d'onde sonore dans le plasma avec une vitesse de c.√3 (onde, qu'il faut imaginer partir du centre du cercle). Au moment de la recombinaison, la surdensité est figée.

Oui ok, une onde sphérique de 0,13Mpc qui va subir l’expansion pour mesurer aujourd’hui 150MPc. Une multiplication d’un facteur z=1100 comme le dit Fabio, son calcul n’ayant pas été contredit, je le prend pour juste. Ce que je dis sur ce point c’est qu’un objet qui est réellement sphérique (dont la surface est formée de points comobiles qui subissent une expansion entre eux) ne sera pas vu de manière sphérique. Or le dessin, montrant des angles de vue et des distances angulaires correspond à ce qui est vu.

Je ne répond que par politesse, je ne veux pas polémiquer, je préfère que Fabio reçoive les réponses qu’il attend. Pour ce que j’en vois il fait partie des «courageux» et arrive toujours avec des questions bien précises. Il ne repart pas toujours satisfait et je ne voudrais en être responsable.

A +

[Lansberg]

...comme le dit Fabio, son calcul n’ayant pas été contredit, je le prend pour juste...

Ce n'est pas son calcul, ni son schéma. C'est extrait de publications ArXiv ou autres ! Je vois mal comment on pourrait contredire quoi que ce soit.

Il ne repart pas toujours satisfait et je ne voudrais en être responsable.

Sur cette question des BAO, il n'y a pas de mystères. La séparation en redshift, ∆z, permet de calculer H(z) par mesure directe. Et la séparation angulaire (extraite du CMB), delta théta, permet de calculer la Da pour tout z.
Ce qui fait des BAO des "règles standard" pour étudier l'expansion, du CMB à l'univers récent.
Ce court article résume assez bien l'intérêt des BAO : http://galaxies-cosmology-2015.wikid...c-oscillations

[yves95210]

Salut,

Ce que je dis sur ce point c’est qu’un objet qui est réellement sphérique (dont la surface est formée de points comobiles qui subissent une expansion entre eux) ne sera pas vu de manière sphérique. Or le dessin, montrant des angles de vue et des distances angulaires correspond à ce qui est vu.

Effectivement. Mais dans l'univers récent (les mesures permettant de déterminer le sound horizon grâce à la corrélation entre les densités de galaxies utilisent surtout des observations à z<0,5), H(z+Δz)=H(z) à 2% près. Donc la figure sphérique reste une bonne approximation.

Et les cosmologistes sont au courant et en tiennent compte :

The other error in our one-scale-parameter approximation is to treat the line-of-sight dilation equivalently to the transverse dilation. In truth, the Hubble parameter changes differently from the angular diameter distance (the Alcock-Paczynski (1979) effect). For small deviations from Ωm = 0.3, ΩΛ = 0.7, the change in the Hubble parameter at z = 0.35 is about half of that of the angular diameter distance. We model this by treating the dilation scale as the cube root of the product of the radial dilation times the square of the transverse dilation.

(source: Detection of the baryon acoustic peak in the large-scale correlation function of SDSS luminous red galaxies, D. Eisenstein et al.
Voir aussi https://ned.ipac.caltech.edu/level5/...Percival5.html)

[Mailou75]

Bon,

Comme Fabio ne semble pas donner suite je m’autorise à répondre, je n’aime pas paraitre impoli...

Ce calcul : «racine cubique du produit de la dilatation radiale par le carré de la dilatation transversale» est pour le moins étrange car il n’y a aucune «généralité» dans le rapport entre le z et l’allure des dilatations visuelles, au contraire c’est au cas par cas.

Mais je pense que je suis hors sujet depuis le début, si vraiment il s’agit d’observations proches (z~0,35), ce dont je parle c’est peanuts. Je croyais qu’il était question d’observation du CMB, vraisemblablement c’est autre chose, la piste du Sloan Digital Sky Survey devait être la bonne...

Dsl a +