Salut,
C'est exactement ce que je pensais. Se mettre d'accord, ça n'arrive pas toujours et dans ce cas inutile d'insister, quand ça passe pas, ça passe pas. Tout le monde n'y arrive pas (surtout dans un domaine un peu compliqué comme ici). Mais c'esr utile pour les lecteurs.Envoyé par mach3
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Bonjour à tous
Permettez-moi donc de faire une présentation complète de la position que je défends dans ce débat, dont je rappelle que c’est bien celle de Karl Schwarzschild, et qu’elle n’est donc ni personnelle ni hors cadre, et qu’elle ne fait appel qu’à des connaissances élémentaires en mathématiques, et à des éléments sourcés dans les discussions précédentes.
Comme mach3 et Deedee81 le souhaitent, elle se veut répondre au vœu implicite des lecteurs silencieux (qui peuvent s’étonner de la voir qualifiée de n’ « importe quoi » sans que jamais soit dénoncé l’argument, (qui devrait être grossier), qui la disqualifierait, alors que le « décortiquage » de mach3 concluait à la qualité du travail de KS.
Je m’excuse à l’avance de l’aspect didactique, trivial et scolaire de ce qui se veut une démonstration mathématique, mais il me semble nécessaire de la présenter aux lecteurs silencieux sous sa forme la plus facile à suivre, et en donner à mes contradicteurs la vision la plus « décortiquée » dans laquelle ils ne manqueront pas de relever et condamner le « n’importe quoi » leur permettant de solder de façon incontestable la querelle en leur faveur, ce qui est j’imagine leur vœu le plus cher.
Etape 1 : illustrer quelque chose de mathématiquement impossible
Si on se place dans le réel, ce qui est un présupposé des calculs algébriques relatifs à notre espace temps, les dérivées des grandeurs locales, ici des longueurs ou des durées, sont représentées par des vecteurs réels dont les carrés scalaires ne peuvent pas être mathématiquement négatifs. Par contre, rien n’interdit à la métrique traitant de ces carrés de vecteurs de produire des changements de signe dans les coefficients affectant ces produits scalaires.
C’est exactement ce qui se passe ici de part et d'autre de Rs.
Pour l'illustrer, prenons l’expression de la métrique la plus simple, celle où les trajectoires se situent sur la composante radiale, ( θ et φ nuls), et où ces trajectoires sont réelles pour r >Rs, lorsqu’on adopte la signature +---, (qui se réduit alors à +-), et qui s’écrit alors :
ds^2 = dτ^2 = [(1- Rs/r)] dt^2 – [1/(1- Rs/r)] dr^2, soit encore plus simplement:
ds^2 = dτ^2 = [A] dt^2 – [1/A] dr^2 (1)
Passons maintenant à r < Rs
ds^2 = dτ^2 = [-A] dt^2 – [-1/A] dr^2 (2)
La métrique n’a pas changé, les crochets ont changé de signe. Sachant que l'expression (1) de la métrique se vérifie formellement et sur le plan du réel, l’algèbre élémentaire ne nous donne aucune possibilité de réécrire formellement avec des nombres réels une expression (2) qui se vérifierait dans le réel :
On aurait le choix entre :
ds^2 = dτ^2 = [-A] i^2 * dt^2 – [-1/A] i^2 * dr^2
(un temps propre, réel quotient de durée et trajectoire imaginaires)
ou, plutôt, puisque dt^2 et dr^2, étaient bien réels dans l’équation (1):
ds^2 * i^2 = dτ^2 * i^2 = [-A] dt^2 – [-1/A] dr^2
( un temps propre imaginaire quotient de durée et trajectoire réelles)
Dans les deux cas, l’espace temps est imaginaire pour r < Rs
Etape 2 Comment peut-on donc se passer de la notation en nombres complexes qui sanctionne un espace imaginaire ?
2 - 1 La convention n’a rien à voir là dedans
La vraie astuce est de faire accepter une double écriture de la métrique.
La méthode de présentation consiste à prétexter une certaine impuissance de l’algèbre, et qu’il existerait une « séparation » de l’écriture et du sens de la métrique, présentée ici comme une « homonymie » qui se répercuterait sur les « morceaux » d’espace temps.
L’étonnant est alors que des différences fondamentales sont exprimées quant à ces deux morceaux d’espace temps, et la manipulation la plus énorme est que l’affirmation de l’appartenance de ces deux morceaux au même espace temps reposerait précisément sur l’une de ces différences :
l’un des morceaux, contrairement à l’autre qui serait fixe, serait de type stationnaire, (en contradiction complète avec l’hypothèse de fixité posée par KS, et après que cette hypothèse de fixité ait été grossièrement inversée en stationnarité), ce morceau stationnaire hors hypothèse KS permettant précisément de montrer l’unicité par un « examen plus approfondi » qui n’est pas présenté.
2 – 2 Ayant affirmé la réalité de la double écriture, il faut donc maintenant montrer la réalité de son existence
Le reste est différent : le domaine de définition de r est différent, les genre des coordonnées r et t sont différents, on a stationnarité, symétrie sphérique et platitude asymptotique dans l'un et non stationnarité et symétrie cylindro-sphérique dans l'autre….
…..Un seul des deux, celui en, est une solution au problème que Schwarzschild a souhaité résoudre initialement, à savoir déterminer la géométrie d'un espace-temps vide, stationnaire, de symétrie sphérique et asymptotiquement plat….
….L'examen plus approfondi, notamment en relâchant la contrainte sur la nullité des termes rectangles lors de la résolution, comme l'a fait Painlevé par exemple, montre cependant que ce n'est pas le cas et qu'il s'agit de deux morceaux du même espace-temps, des morceaux disjoints certes, mais bien du même espace-temps.
m@ch3
Cette double écriture, sur laquelle aucune publicité n’est faite, est cependant bien présente, sans justification, dans la discussion (fermée) « Jamais rien ne tomba dans un trou noir ?, # 111, page 4.
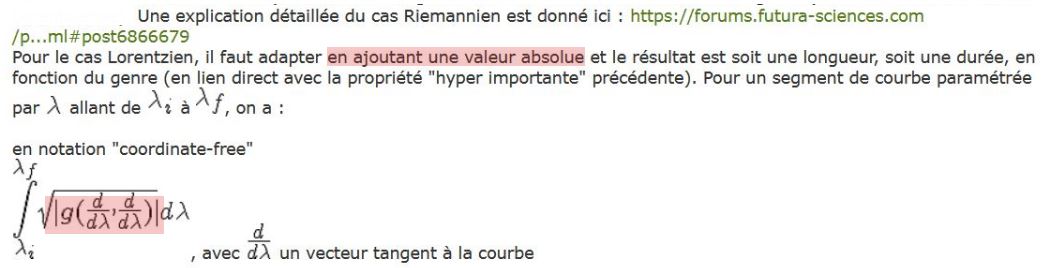
La remarque importante est que les valeurs absolues incluent les coefficients, astuce qui rend possible, subrepticement, d'effacer, en tant que de besoin, le changement de signe gênant de ces coefficients de part et d’autre de Rs, de se passer ainsi des nombres complexes, de faire passer pour fantaisies dépassées la rigueur des algébristes du passé, et de réintégrer mathématiquement la sphère de Schwarzschild dans l’espace temps réel.
2 – 3 Et la convention dans tout ça:
Elle joue un rôle totalement subalterne : elle permet simplement de faire porter l’écriture fautive sur le membre de l’équation (ou le côté de Rs) que l’on désire, et en cela je suis en parfait accord avec ThM55 dans son #16, quand il dit qu’elle n’a aucune importance !
3 – Complément dimensionnel : on a présenté ici l’aspect algébrique du débat, qui est le terrain choisi par mach3, mais il ne faudrait pas oublier l’aspect dimensionnel de la position académique qui accolerait en continuité notre monde, réel, à 3 dimensions spatiales et une temporelle avec un autre, monde, surréaliste, à 3 dimensions temporelles pour une seule spatiale !
Dernière modification par bernarddo ; 08/02/2022 à 15h53.
Ben si, c'est justement l'intérêt d'une forme quadratique Lorentzienne, de donner des signes opposés aux carrés scalaires des vecteurs de genre temps et de genre espace. Ensuite :
- si on a choisi la signature -+++, la durée correspondante à un vecteur de genre temps s'obtient en prenant la racine carré de l'opposé du carré scalaire de ce vecteur de genre temps, et la longueur correspondante à un vecteur de genre espace s'obtient en prenant la racine carré du carré scalaire de ce vecteur de genre temps.
- si on a choisi la signature +---, la durée correspondante à un vecteur de genre temps s'obtient en prenant la racine carré du carré scalaire de ce vecteur de genre temps, et la longueur correspondante à un vecteur de genre espace s'obtient en prenant la racine carré de l'opposé du carré scalaire de ce vecteur de genre temps.
Cela a déjà été expliqué, et tant que ça ne sera pas compris et digéré, on n'avancera pas.
Je ne prends même pas la peine de lire la suite pour l'instant, vu que la première affirmation est fausse.
m@ch3
Never feed the troll after midnight!
charabia totalement incompréhensible ....La remarque importante est que les valeurs absolues incluent les coefficients, astuce qui rend possible, subrepticement, d'effacer, en tant que de besoin, le changement de signe gênant de ces coefficients de part et d’autre de Rs, de se passer ainsi des nombres complexes, de faire passer pour fantaisies dépassées la rigueur des algébristes du passé, et de réintégrer mathématiquement la sphère de Schwarzschild dans l’espace temps réel.
Si on considère une ligne d'univers, alors en signature +---, cela exige :
Donc :
Et donc
soit :
Si
Si
Graphiquement cela se voit aux cônes de lumière qui sont "couchés" dans la région r<Rs (voir par exemple : https://physics.stackexchange.com/qu...schild-horizon ).
Il n'est aucunement question d'imaginaires, il faut vraiment arrêter avec ça.
Au stade où on en est, il n'est justement pas question de statuer sur l'appartenance de ces deux morceaux à un même espace-temps. Pour cela, il faut s'intéresser à la résolution du problème de Schwarzschild en relâchant la contrainte des termes rectangles nuls (c'est ça l'examen plus approfondi), puis montrer que les solutions obtenues, dont la plupart sont sans singularité de coordonnée en r=Rs, sont toutes équivalentes, et qu'elle contiennent les deux morceaux décrits par l'expression de Schwarzschild.L’étonnant est alors que des différences fondamentales sont exprimées quant à ces deux morceaux d’espace temps, et la manipulation la plus énorme est que l’affirmation de l’appartenance de ces deux morceaux au même espace temps reposerait précisément sur l’une de ces différences :
l’un des morceaux, contrairement à l’autre qui serait fixe, serait de type stationnaire, (en contradiction complète avec l’hypothèse de fixité posée par KS, et après que cette hypothèse de fixité ait été grossièrement inversée en stationnarité), ce morceau stationnaire hors hypothèse KS permettant précisément de montrer l’unicité par un « examen plus approfondi » qui n’est pas présenté.
Sinon, question vocabulaire, fixe = stationnaire. Le morceau avec r>Rs est stationnaire, ou fixe, ou encore statique, formellement, les coefficients de la métrique sont indépendant de la coordonnée temporelle, qui est t dans ce morceau. Le morceau r<Rs est dynamique, le contraire de statique, formellement, les coefficients de la métrique sont dépendant de la coordonnée temporelle, qui est r dans ce morceau.
Il n'y a pas de norme définie sur l'espace-temps, parce que la forme quadratique est indéfinie (il y a des carrés scalaires de deux signes), mais on peut définir une norme sur les sous-espaces, pourvu que la forme quadratique y soit définie (les carrés scalaires des vecteurs du sous-espace considéré sont tous de même signe). La définition de la norme dépend alors du signe de la forme quadratique et il y en a donc deux différentes :La remarque importante est que les valeurs absolues incluent les coefficients, astuce qui rend possible, subrepticement, d'effacer, en tant que de besoin, le changement de signe gênant de ces coefficients de part et d’autre de Rs, de se passer ainsi des nombres complexes, de faire passer pour fantaisies dépassées la rigueur des algébristes du passé, et de réintégrer mathématiquement la sphère de Schwarzschild dans l’espace temps réel.
Par simplification d'écriture, on peut utiliser une formule unique :
Mais personne n'a jamais dit ou écrit un truc pareil!!! il n'y a toujours qu'une dimension temporelle et 3 dimensions spatiales.3 – Complément dimensionnel : on a présenté ici l’aspect algébrique du débat, qui est le terrain choisi par mach3, mais il ne faudrait pas oublier l’aspect dimensionnel de la position académique qui accolerait en continuité notre monde, réel, à 3 dimensions spatiales et une temporelle avec un autre, monde, surréaliste, à 3 dimensions temporelles pour une seule spatiale !
m@ch3
Never feed the troll after midnight!
Un mot est réfutable dans l’extrait ci-dessus : c’est le mot « expliqué », que j’aurais tendance à remplacer par le mot « asséné » associé également avec un de vos qualificatifs favoris « ad nauseam ».
Je réclame une explication qui n’a jamais encore été donnée dans ces échanges et qui me semble fondamentale :
Comment se fait-il qu’une discipline comme l’algèbre différentielle, ici dans sa composante « variétés », qui n’est censée conduire que des développements purement mathématiques sur des objets également purement mathématiques, ici plus précisément des vecteurs, et dans son langage spécifique, pourrait voir ces développements perturbés par des notions complètement étrangères à ce langage, ici la notion de genre, au point de perdre tout ce qui fait sa force, sa capacité formelle à distinguer le vrai du faux qui lui donne son rapport si particulier au réel. Perte reconnue bien plus honnêtement, quoique implicitement, dans l'inexistante mais avouée dissociation de l'écriture et du sens dans le #17 de ce fil.
On voit bien, par contre, la capacité de double écriture qui résulte de cette prétendue propriété, qui permet de remplacer, au besoin, le carré par son opposé, et permet de réintroduire, en plus et en parallèle de la notation classique i^2, la notation (-1)^1/2 dont on sait bien tous, depuis qu’on a eu 13 ou 14 ans, que sa définition n’est pas cohérente avec la propriété : [(a)^1/2]^2 = (a^2)^1/2
La réalité est celle-ci : la métrique d’un espace-temps réel impose d’y trouver exprimés, en même temps et en nombres réels, des carrés de temps propre réel, de temps réellement écoulé et de trajectoire réellement effectuée.
La démonstration en a été faite que c’était impossible pour [0 < r < ∞], et que le recours aux imaginaires était nécessaire pour r < Rs. Veuillez croire que je regrette infiniment d’avoir à rappeler à des mathématiciens spécialistes quelle est la violation de la règle mathématique qui a permis de contourner cette impossibilité.
Le mieux dans ce cas est de consulter de vrais cours. Par exemple celui-ci : http://perso.math.u-pem.fr/Fkloeckne...Euclidiens.pdf
m@ch3
Never feed the troll after midnight!
effectivement je ne pense pas qu'écrire des équations réponde au problème de Bernarddo. Les équations il les connait, mais il les interprète de travers. Donc les réécrire , sous une forme ou une forme différente, ne va pas l'aider. Il faut comprendre l'origine de son erreur conceptuelle (pour moi c'est qu'il continue à penser qu'un observateur peut rester à "r = constante" pour r< Rs, alors que c'est impossible, mais je n'ai peut etre pas compris son point).
Bonjour
Le fond du problème est une méprise sur la signification de ds²:
Voir commentaire de S. Carroll (Cours de RG au MIT)
Perhaps this is a good time to note that most references are not sufficiently picky to
distinguish between “dx”, the informal notion of an infinitesimal displacement, and “dx”,
the rigorous notion of a basis one-form given by the gradient of a coordinate function.
In fact our notation “ds² ” does not refer to the exterior derivative of anything, or the square of
anything; it’s just conventional shorthand for the metric tensor.
On the other hand, “(dx) ² ” refers specifically to the (0, 2) tensor dx ⊗ dx
L'expression du ds², c'est la description du tenseur métrique en géométrie analytique sur une variété.
Cordialement
Salut,
En y repensant, je pense que tu as raison. Merci pour la référence.
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
L'une des raisons de cette écriture est de pouvoir faire des manipulations "intuitives" (mais du coup peu rigoureuses, même si le résultat final est correct), comme celles que j'effectue au début du message 35 ( https://forums.futura-sciences.com/d...ml#post6910298 ) pour encadrer dr/dt.
En effet si on veut faire la même chose en étant rigoureux, c'est beaucoup plus lourd, bien que je l'ai déjà fait dans certains posts... Par exemple en toute rigueur on ne peut pas faire le rapport de dr² par dt² et dire que c'est le carré de dr/dt, vu que ce sont des tenseurs et pas des nombres. Et on ne peut pas non plus poser
m@ch3
Never feed the troll after midnight!
BonjourL'une des raisons de cette écriture est de pouvoir faire des manipulations "intuitives" (mais du coup peu rigoureuses, même si le résultat final est correct), comme celles que j'effectue au début du message 35 ( https://forums.futura-sciences.com/d...ml#post6910298 ) pour encadrer dr/dt.
En effet si on veut faire la même chose en étant rigoureux, c'est beaucoup plus lourd, bien que je l'ai déjà fait dans certains posts... Par exemple en toute rigueur on ne peut pas faire le rapport de dr² par dt² et dire que c'est le carré de dr/dt, vu que ce sont des tenseurs et pas des nombres. Et on ne peut pas non plus poser
m@ch3
Bien entendu, quand on fait les calculs, on peut oublier cela. C'est l'intérêt "simplificateur" de la géométrie analytique, on travaille sur les composantes (on oublie que ce sont des composantes sur une base de tenseurs) et cela marche très bien. Ma remarque c'était pour répondre aux états d'âme de Bernarddo, comme le fait qu'il y aurait des "carrés" négatifs donc des "grandeurs" imaginaires.
Cordialement
Il semble y avoir une confusion entre mathématiques et réalité. En maths on pose des axiomes, qu'on tient pour vrais, puis on démontre des propositions qui sont alors vraies, ou au contraire ou démontre que certaines propositions sont fausses, ceci indépendamment de toute "réalité".
Ce sont les sciences physiques qui font le lien entre un modèle mathématique choisi à dessein (voire construit à dessein) et la réalité, qui apparient tel variables abstraites avec telles observations concrètes et ceci d'une façon bien précise. Quand on postule une théorie physique, on suppose que les observations concrètes vont être en accord avec un modèle mathématique, c'est à dire qu'elles vont s'articuler entre elles de façon isomorphe à la façon dont les variables abstraite du modèle s'articulent entre elles. Tout désaccord étant invalidant pour le modèle, ou a minima, restreignant sont domaine d'application.
Quand on travaille sur une variété Lorentzienne, c'est à dire une variété pseudo-riemannienne dont les tangents sont munis d'une forme quadratique lorentzienne, il est d'usage, même en mathématiques pures, non appliquées, de parler de vecteur de genre temps pour les vecteurs dont le carré scalaire est de signe minoritaire et genre espace pour ceux dont le carré scalaire est de signe majoritaire. Cet usage dérive simplement du fait qu'une variété de ce type est impliquée dans la modélisation de l'espace-temps en physique et que dans ce cadre il est associé à un vecteur de genre temps, abstrait, une mesure de durée, concrète, et à un vecteur de genre espace, abstrait, une mesure de longueur, concrète. On aurait très bien pu utiliser à la place les termes de vecteur "positif" et de vecteur "négatif" par exemple, ou de vecteur "normal" et de vecteur "antinormal". Peu importe le nom, du moment que c'est défini. Après autant donner un nom qui va simplifier les usages si c'est utilisé par différentes catégories de personnes.
Par des règles qui sont propres aux mathématiques pures, on peut définir une norme pour le genre temps et une norme pour le genre espace. Et cela sans se soucier d'une quelconque réalité.
Ensuite, le physicien, en cherchant un modèle mathématique qui pourra s'accorder avec les observations, va utiliser les définitions incluses dans le modèle, et décider des bonnes associations entre variables abstraites et observations concrètes (les "bonnes" dans le sens celle qui vont donner le meilleur accord). Il se trouve qu'associer les durées avec les normes des vecteurs de genre temps et les longueurs avec les normes des vecteurs de genre espace, ça marche, c'est à dire que l'accord entre observations et prédictions est bon.
Notons tout de même que ce qui précède est schématique et linéaire, pour simplifier l'idée, parce qu'en réalité, les mathématiques ne sont pas toujours développées en amont d'une théorie, mais parfois conjointement avec la théorie. Il n'en reste pas moins que le modèle mathématique utilisé, même si développé au fur et à mesure du besoin, reste un objet purement mathématique parfaitement rigoureux, logique, cohérent (dans le cas contraire, il est forcément abandonné, car capable de prédire une chose et son contraire une fois utilisé dans une théorie physique). Les objets qu'il contient peuvent porter des noms chargés de sens physique (genre temps, ligne d'univers, ...), cela ne changera rien à la rigueur du modèle.
Par exemple, l'affirmation "une courbe de t,
On peut ensuite prédire ce que cette proposition signifie en terme d'observations, c'est à dire quelles mesures feraient un observateur dans une région de l'espace-temps décrite par cette expression de la métrique, par exemple, le long d'une ligne d'univers de t,
m@ch3
Never feed the troll after midnight!
l'incorrection mathématique traverse toute la physique. Par exemple un physicien aura tendance à penser que f est un nombre et que f(t) est une fonction, alors qu'un mathématicien pensera l'inverseL'une des raisons de cette écriture est de pouvoir faire des manipulations "intuitives" (mais du coup peu rigoureuses, même si le résultat final est correct), comme celles que j'effectue au début du message 35 ( https://forums.futura-sciences.com/d...ml#post6910298 ) pour encadrer dr/dt.
En effet si on veut faire la même chose en étant rigoureux, c'est beaucoup plus lourd, bien que je l'ai déjà fait dans certains posts... Par exemple en toute rigueur on ne peut pas faire le rapport de dr² par dt² et dire que c'est le carré de dr/dt, vu que ce sont des tenseurs et pas des nombres. Et on ne peut pas non plus poser
m@ch3.
Salut,
C'est vraiPar exemple un physicien aura tendance à penser que f est un nombre et que f(t) est une fonction, alors qu'un mathématicien pensera l'inverseCeci dit quand je lis des livres ou articles de physique je préfère franchement la rigueur (quand elle est possible) et les conventions des mathématiciens, je trouve ça plus clair (les conventions des physiciens ne sont pas seulement parfois différentes mais parfois aussi différents auteurs suivent différentes conventions). Mais c'est une appréciation personnelle.
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Bonjour à tous
Je suis donc toujours considéré dans l’erreur sans que mes considérations sur l’écriture de la métrique du # 32 aient été contestées sur le plan formel. Il y a des objections de diverses natures auxquelles je me dois de répondre
On trouve maintenant trois positions :
1 - Mach3 me renvoie à un nouveau manuel de RG: ma réponse est que considère comme suffisant de me référer à Adler, d’autant que j’y trouve, sous une autre forme, des libertés prises avec les mathématiques, page 193, des exponentielles négatives, que je reproduis ici :
exponéga.JPG
Il faudra donc m'opposer un cours dont je pourrai être sûr qu'il est exempt de licences de ce type pour r < 2m.
2 - Ordage, rejoint par Deedee, retrouve un argumentaire déjà utilisé par mach3 :
simpliste.JPG
Ce qui est surprenant, avec cette référence prestigieuse, c’est le vide sidéral (et j’allais dire MITeux), de sa démonstration,
entre la suffisance et le truisme de sa première partie portant sur le « dx » où, il explique que peu de travaux de référence sont suffisamment pointus pour faire la différence entre « dx » comme expression « libre » d’un déplacement infinitésimal (donc apparemment supposée discutable) et la formulation rigoureuse du gradient d’une fonction bien définie (qui serait évidemment inattaquable), situation que je trouve pour le moins heureuse puisqu’il s’agit évidemment strictement de la même chose.
et le hors sujet de son explication finale, (sur son carré, dx^2 ou ds^2), qui ne serait qu’un raccourci sténo pour exprimer la définition même du tenseur métrique, ce qui n’explique strictement rien.
Y aurait-il outrage à lui demander alors de préciser ce qui sépare structurellement, (au moins en l’absence de termes croisés), son dx^2, du carré de la distance temporelle entre deux évènements dτ^2, auquel l’égale la formule de la métrique, pourquoi serait-il différent du carré de leur distance spatiale, et de donner quelques éclaircissements sur ce qui viendrait casser la symétrie observée dans les termes de la métrique ?
3 Archi3 n’intègre pas le problème formel d'impossibilité d'écrire des équations (1) et (2) simultanément vérifiées avec des nombres réels.
Il tente une explication selon laquelle je verrais un observateur fixe à r = cte pour r < Rs. Je le rassure. Un tel observateur, fictif, puisqu’il ne saurait avoir une masse qui modifierait alors l’hypothèse de KS, serait au contraire animé d’une vitesse supraluminique, si un tel univers existait vraiment. L’explication est toute simple : admettons que c double, Rs est alors divisé par 4, et la vitesse (pseudo)photonique sur cette nouvelle sphère réduite sera de 2c. Il y a comme un hic.
Tout ceci est parfaitement cohérent avec l’aspect « intrinsèquement dynamique » de l’intérieur de la sphère de Schwarzschild, revendiqué par Kip Thorn, si seulement un espace temps existait là.
je ne sais pas pourquoi tu as changé le signe de "A" en entre (1) et (2), l'équation
ds^2 = dτ^2 = [(1- Rs/r)] dt^2 – [1/(1- Rs/r)] dr^2
est la même qu'on soit à r>Rs ou à r< Rs. C'est l'interprétation physique de r et de t qui est différente, mais la forme de la métrique reste la même.
considère comme suffisant de me référer à Adler, d’autant que j’y trouve, sous une autre forme, des libertés prises avec les mathématiques, page 193, des exponentielles négatives
Incroyable de vouloir imposer son point de vue sur une solution de la relativité générale sans connaître une chose aussi élémentaire...
On en est là.
m@ch3
Never feed the troll after midnight!
Bonjour
Oui ds² désigne le tenseur métrique de type {0,2}.
Quant aux "dx²", c'est une notation générique: x, représente n'importe laquelle des coordonnées (x, y, z, t), A noter que la forme est générale et représente tous les types de termes (quadratiques ou croisés). Ne pas se laisser égarer par la notation générique. Toi qui semble aimer les solutions mathématiques rigoureuses, la rigueur mathématique c'est cela.
L'eusses-tu cru?
Cordialement
Les deux exponentielles sont ici tracées sans trace de négativité.
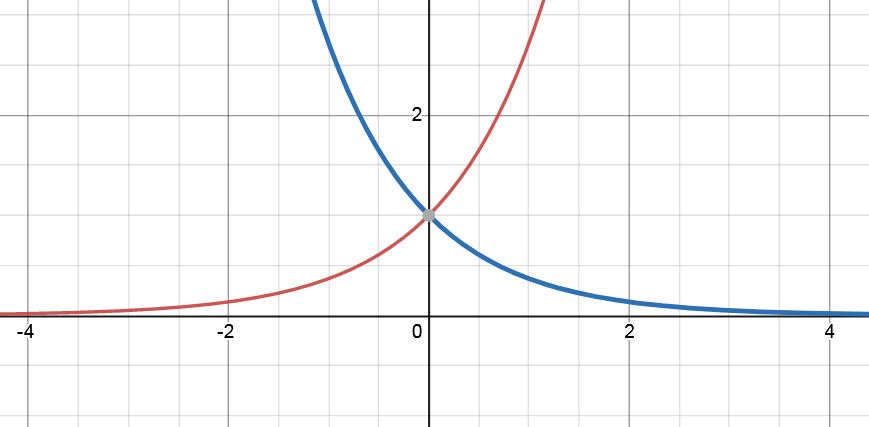
Mettons cette bêtise sur le fait qu'Adler est normalement inattaquable et que le prendre en faute a été tellement incroyable que cela a été écrit sous le choc et sans vérifier. Cela m'est aussi arrivé et je peux le comprendre.
Mais le résultat est là, y réfléchir devient maintenant indispensable !!!
J'aurais dû préciser qu'il s'agissait simplement d'une double écriture montrant le changement (de signe) qui s'opérait sur les valeurs numériques des coefficients des carrés dans le second membre entre (1) et (2).
Et donc que cette inversion de signe devait également se produire sur les coefficients du premier membre pour respecter l'unicité de la métrique.
Et que cela imposait naturellement l'utilisation d'imaginaires sur les coefficients du premier membre.
L'interprétation physique ne peut se faire qu'après avoir satisfait à l'exigence mathématique d'équilibrage de l'équation.
En l'occurrence que les carrés du premier membre sont imaginaires. Que cette interprétation porte d'abord sur la question du réel et de l'imaginaire. Et donc que la métrique décrit un espace temps imaginaire pour r < Rs
Nota: si on avait utilisé une signature inversée, la même opération aurait montré que l'espace temps aurait été imaginaire pour r > Rs. Ce qui est incompatible avec l'espace temps qui nous baigne et ne peut être imaginé. Cela montre qu'il n'y a qu'une signature possible pour cette métrique
Sacré "imaginaire"... victime d'une dénomination dont certains (comme Bernardoo) la prennent au pied de la lettre...
Mathématiquement, un nombre imaginaire n'est pas moins «réel» qu'un nombre "réel" habituel. Il n'y a que les règles algébriques qui changent.
Vous vous êtes laissé abuser par une dénomination, faut y revenir un moment donné...Que cette interprétation porte d'abord sur la question du réel et de l'imaginaire
Avant de parler de relativité, sachez que les nombres complexes (je vous laisse chercher la relation) participent grandement à toutes les technologies basées sur l'électricité à partir du XIXème siècle, donc cette "astuce" mathématique est bien ancrée dans le "réel". Bon, je sais que c'est en vain de vous dire ça...pas grave, cela pourra peut-être servir à d'autres.
je ne comprends pas pourquoi, c'est quoi que tu appelles "les coefficients du premier membre" ? (si tu veux dire qu'il faut changer ds^2 en - ds^2 sous prétexte que les coefficients de la métrique ont changé de signe, c'est évidemment faux, le ds^2 a toujours la même expression, ça ne change pas de signe, c'est ce que je viens te dire).
La question d'ordre psychologique, c'est pourquoi, si tu constates que tu n'es pas du même avis que l'ensemble des spécialistes, tu postules que c'est toi qui as raison et l'ensemble des spécialistes à tort, et pas l'inverse ? et que tu aurais pu simplement mal comprendre parce que tu n'es pas particulièrement un expert du domaine ?
Reprenons les choses de façon encore plus élémentaire, je m’excuse de la lourdeur que cela entraîne)
Mettons-nous d'accord sur le fait que:
1 – Sur le fait que ds^2, dτ^2, dt^2, dr^2 sont des expressions de carré qui peuvent être en toute généralité réels ou imaginaires, mais qu'il faut qu'ils soient réels pour que dans ℝ,on puisse écrire: ds^2 = ds * ds, dτ^2 = dτ * dτ, dt^2 = dt * dt, dr^2 = dr *dr.
2 - Pour r > Rs, la métrique s’écrit de façon simplifiée [1- Rs/r] = [A]
ds^2 = dτ^2 = [A] * dt^2 – [1/A] * dr^2 (1)
Nous avons considéré que l’équation est vérifiée numériquement et que, dans ce domaine r > Rs, le temps élémentaire dt et le déplacement élémentaire dr sont réels et peuvent s’écrire dt *dt et dr * dr (et que cela entraîne que les carrés du premier membre sont aussi réels), et que l’on peut écrire l’équation :
ds * ds = dτ * dτ =[A] * dt *dt – [1/A] * dr * dr (1 bis)
3 – Pour r < Rs, la quantité A change de signe, la même écriture dans les deux membres donnerait :
ds * ds = dτ * dτ = -[A] * dt *dt + [1/A] * dr * dr (2 ?)
Une telle équation, qui vérifie aussi (1 bis) et qui serait correctement écrite, est-elle toujours numériquement vérifiée, ce qui prouverait que nous sommes dans le même espace temps ?
A l’évidence le second membre ayant changé de signe, le premier doit également le faire pour que la vérification s’étende à r < Rs.
L'écriture n'était pas correcte.
La seule expression mathématique correcte est donc d’écrire :
i ds * i ds = i dτ * i dτ = -[A] * dt *dt + [1/A] * dr * dr (2bis)
Ce qui introduit un écart spatial et un temps propre imaginaires, ce qui est incompatible avec notre exigence relative à l’appartenance au même espace temps.
Nota : il est particulièrement éclairant de voir comment Adler résout le problème (dans la réponse à mach 3) :
On peut voir simplement sur la position attribuée aux exponentielles dans la métrique son refus d’entériner le changement de signe du second membre en niant celui des exponentielles. (page 187 du manuel)
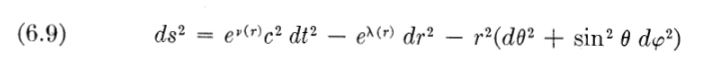
Le constat est cruel, Adler raterait son bac math élèm
Mais ds^2, dt^2 et dr^2 ne sont pas des réels, et encore moins des imaginaires. Ce ne sont pas des scalaires. Ce sont des tenseurs, des applications bilineaires qui transforment un couple de vecteur en un nombre réel.
Et ds, dt, dr ne sont pas non plus des réels ou des imaginaires. Ce ne sont pas des scalaires non plus. Ce sont des formes linéaires, qui transforment un vecteur en nombre réel.
m@ch3
Never feed the troll after midnight!
L'écriture est tout à fait correcte. Si tu veux dire que pour le même couple de valeur de (dr, dt), le signe de ds^2 (c'est à dire l'application de la 2-forme à (dr,dt) ) change, c'est vrai. Mais c'est justement parce que dr et dt ont changé de nature. La même valeur de dr et dt peut correspondre à un intervalle du genre temps pour r>Rs et du genre espace pour r<Rs . Mais l'écriture de la métrique reste formellement la même.
Encore une fois, une fois constaté une divergence (objective) entre ce que tu penses et ce que disent les livres, pourquoi ne te dis tu pas "j'ai pas du comprendre quelque chose, est ce que vous pouvez m'expliquer ?" plutot que "tous les physiciens sont des cons et moi seul j'ai raison" ?
On aurait pu s'attendre à acter la réalité de la licence prise par Adler par rapport aux mathématiques, et de la nécessité d'une réflexion de ce que qu'elle pourrait avoir comme conséquences sur la rigueur de sa démonstration.
Et là on trouve au contraire une réflexion, confinant à l'incompréhensible, conjuguant la confusion, le contradictoire et la censure implicite. Détaillons:
La confusion:
elle s'établit entre le concept et sa mesure!
Admettons que ds, dt, dr soient des formes linéaires: il s'agit là de la définition d'un concept.
Le problème est que, introduits dans un calcul, il faut bien que ces concepts prennent des valeurs numériques dans les expressions où ils interviennent. Si on ne pouvait pas le faire, on se trouverait devant l'impossibilité absolue de les utiliser.
C'est ce qui se passerait si on ne pouvait pas les exprimer sous forme de nombres réels ou imaginaires! L'affirmation "ni réel, ni imaginaire", est donc fausse et résulte donc de la confusion entre la définition du concept et sa mesure.
Le contradictoire:
La suite nous apprend que ce concept permet de transformer un vecteur en nombre réel.
Euréka, l'affirmation précédente, ni réel, ni imaginaire était donc un joke, au moins pour le réel. Décidément, il faut suivre !!
La censure implicite:
C'était Ok pour le réel, mais pourquoi pas l'imaginaire ? Parce qu'on affirme par ailleurs qu'on n'a pas besoin ? Pourquoi ne pas réexaminer les calculs, d'autant qu'on a vu qu'Adler avait pris des libertés avec les maths ?. Et que les anciens y avaient eu recours. Et qu'il n'y a pas consensus.
Bernarddo, tu n'as pas tenté de répondre à la question suivante :
Plusieurs points:
- la divergence est entre ce que j'écris et ce que disent (écrivent) les livres. Si j'ai tort, alors il suffit de le démontrer puisque tout est écrit.
- j'ai au contraire montré qu'un livre de RG qui fait autorité est pris en faute mathématiquement sur le point de divergence que j'ai avec la communauté académique, laquelle a entériné l'erreur (# 48)
- dire que tous les physiciens sont d'accord est une immense erreur, simplement leurs travaux sont décriés et maintenus dans l'ombre (y compris les travaux originaux de Schwarschild)
- rends moi au moins cette justice que je n'ai fait aucune déclaration ad hominem négative envers mes contradicteurs, alors que la réciproque n'est certainement pas vraie.
Enfin pour amener un peu plus de réflexion, j'aimerais être éclairé sur le problème que j'ai avec l'expression "l'opposé d'un carré" , expression qui joue un rôle clé dans la propriété fondamentale qui m'est assénée et que je n'arrive pas à comprendre. Personnellement, "l'opposé d'un carré", je ne sais pas ce que c'est.
Comme dirait Coluche, "je me doute" que ce serait un carré qu'on pourrait écrire [-a]
Et là, j'ai comme l'impression qu'il faudrait accepter qu'on puisse écrire:
(-a)^1/2 * (-a)^1/2 = [(-a)^1/2]^2 = (-a)^1 = - a (définition qui malheureusement ne respecte pas le résultat correct: a
J'ouvre un concours pour en trouver une définition mathématiquement correcte qui n'aurait pas recours aux imaginaires
Dernière modification par bernarddo ; 13/02/2022 à 16h01.
ben on a relevé de multiples erreurs dans ce que tu dis
ds n'est pas une forme linéaire, ds^2 est une forme quadratique, ce n'est pas du tout la même chose.
