Signature(s) de la métrique de Schwarzschild et invariance des lois physiques

[mach3]

ds n'est pas une forme linéaire

C'est moi qui l'ait dit que ds était une forme linéaire. N'est ce pas le cas (même si l'écriture est abusive) ? Par contre dr et dt sont bien des formes linéaires.

m@ch3
-----

[Archi3]

C'est moi qui l'ait dit que ds était une forme linéaire. N'est ce pas le cas (même si l'écriture est abusive) ? Par contre dr et dt sont bien des formes linéaires.

m@ch3

ben non ds ne s'exprime pas comme une combinaison linéaire de composantes de 4-vecteurs (pas plus que la distance n'est linéaire par rapport aux coordonnées).

[mach3]

ben non ds ne s'exprime pas comme une combinaison linéaire de composantes de 4-vecteurs (pas plus que la distance n'est linéaire par rapport aux coordonnées).

Même si s est le paramètre d'une courbe ?

m@ch3

[Archi3]

si tu la restreins à une courbe de dimension 1, oui, mais ce n'est pas une forme différentielle dans l'espace 4D. En revanche tu peux intégrer une forme différentielle 4-D sur une courbe.

[mach3]

La confusion:

elle s'établit entre le concept et sa mesure!

Admettons que ds, dt, dr soient des formes linéaires: il s'agit là de la définition d'un concept.

Le problème est que, introduits dans un calcul, il faut bien que ces concepts prennent des valeurs numériques dans les expressions où ils interviennent. Si on ne pouvait pas le faire, on se trouverait devant l'impossibilité absolue de les utiliser.
C'est ce qui se passerait si on ne pouvait pas les exprimer sous forme de nombres réels ou imaginaires! L'affirmation "ni réel, ni imaginaire", est donc fausse et résulte donc de la confusion entre la définition du concept et sa mesure.

Le contradictoire:

La suite nous apprend que ce concept permet de transformer un vecteur en nombre réel.

Euréka, l'affirmation précédente, ni réel, ni imaginaire était donc un joke, au moins pour le réel. Décidément, il faut suivre !!

La censure implicite:

C'était Ok pour le réel, mais pourquoi pas l'imaginaire ? Parce qu'on affirme par ailleurs qu'on n'a pas besoin ? Pourquoi ne pas réexaminer les calculs, d'autant qu'on a vu qu'Adler avait pris des libertés avec les maths ?. Et que les anciens y avaient eu recours. Et qu'il n'y a pas consensus.

C'est un cours de maths, et en particulier d'algèbre tensorielle qu'il faut.

Pour résumer :
-On part d'un corps K, dont les éléments sont les "scalaires", ou encore tenseurs d'ordre 0.
-On construit un K-espace vectoriel V
-On construit l'espace dual V* qui contient les fonction linéaires de V vers K, les fameuses formes linéaires, ou covecteurs, qui aux vecteurs de V associent des éléments du corps K, des scalaires. V* est lui-même un K-espace vectoriel dont le dual est V, les vecteurs de V étant des fonctions linéaires de V* vers K. Vecteurs et covecteurs sont les tenseurs d'ordre 1.
-On construit ensuite les produits tensoriels de V et V*, qui contiennent les fonctions multilinéaires de Vx...xVxV*x...xV* vers K, ce sont les tenseurs (d'ordre 2 ou plus), qui à un multiplet de vecteurs de V et de covecteurs de V* associent des éléments du corps K.

Dans notre cas, le corps est celui des réels : on utilise donc un R-espace vectoriel, les images des vecteurs par les formes linéaires sont donc des réels, et les images des multiplets de vecteurs et covecteurs par des tenseurs sont donc aussi des réels.
En particulier, l'application du tenseur métrique à un couple de vecteur donne un nombre réel.
Impossible que ce soit autrement parce que les vecteurs utilisés sont des éléments d'un R-espace vectoriel, et donc :
- les formes linéaires appartenant à l'espace dual de ce R-espace vectoriel ne peuvent pas donner autre chose que des réels quand elles sont appliquées à ces vecteurs,
- les formes multilinéaires (les tenseurs d'ordre 2 ou plus, dont le tenseur métrique) appartenant aux produits tensoriels de ce R-espace vectoriel et de son dual ne peuvent pas donner autre chose que des réels quand elles sont appliquées à un multiplet de ces vecteurs et covecteurs.

m@ch3

[ordage]

Bonjour
D'accord avec toi, sur la présentation mathématique formelle à partir d'espaces vectoriels..

Peut-être qu'il faut préciser la terminologie (elle peut varier selon les ouvrages).

Je présente la chose dans le contexte de la relativité générale (espace-temps représenté par une variété pseudo-riemannienne à 4 dimensions).
Il faut rappeler qu’une variété n'a pas (globalement) une structure d'espace vectoriel, mais qu'on peut en définir une en chaque point.

Vecteur: représenté avec un indice haut- dans l'espace "local tangent" à la variété.
Dual-vecteurs: (aussi appelé forme linéaire, représenté avec un indice bas , qui lui est dans l'espace "local co-tangent" à la variété.

A noter que les "vecteurs" et dual vecteurs sont des tenseurs "d'ordre 1", et qu'un scalaire est un tenseur d'ordre 0.

Après pour les tenseurs d'ordre supérieur, qu'on peut construire de différentes manières, ils peuvent être plus complexes, on note le "type" par {i, j} où i est le nombre d'indices "haut" et j le nombre d'indices bas. Ainsi le "tenseur métrique est noté {0, 2}. C'est un dual tenseur d'ordre 2, ( forme bi-linéaire).

Cordialement

[bernarddo]

Bonjour

Il n’y a aucune raison sauf, en situation difficile, à lancer une diversion bienvenue, de revenir à un cours d’algèbre tensorielle, qui n’apportera rien à la plupart des lecteurs silencieux qui n’en maîtrisent pas le code conceptuel, alors que probablement beaucoup ont le niveau de math élèm suffisant qui leur aura permis de vérifier par eux-mêmes qu’il y avait un « loup » mathématique évident dans le manuel d’Adler (utilisations d’exponentielles négatives pour r < Rs). Ils restent donc sur leur faim de connaître le fin mot de l’histoire, et de savoir si cette erreur énorme permettrait malgré tout d’obtenir le résultat correct.

Le cadre du « loup » chez Adler est probablement éloigné des lecteurs silencieux et, pour les satisfaire, il me semble plus logique et pratique de se concentrer sur l’ « explication » de mach3 qui a le même objectif et la même logique, celle d’étendre le réel à l’intérieur de la sphère de Schwarzschild, car il est possible d’expliquer de façon bien plus simple le coup de baguette magique que permet sa « convention » pour faire disparaître ce « loup » du paysage, sans avoir à s’expliquer sur son existence chez Adler !

On repart de sa fameuse « propriété hyper importante à la base de tout le reste »

Capture.JPG

Considérons-en une seule facette, par exemple celle-ci, l’autre n’en étant que le symétrique : elle s’écrit de façon équivalente et plus explicite :

Si la signature est +---, le carré scalaire d’un vecteur de genre temps donne le carré de la durée propre qu’il représente, et si la signature est -+++, il donne l’opposé du carré de cette durée propre.

On en déduit donc que l’écriture de ce carré scalaire dans la première signature ( carré scalaire foncièrement réel en tant que carré d’une durée réelle, que l’on peut écrire [a^2]) donne donc, à l’opposé du carré de cette durée, que l’on écrira donc [– a^2], et via la seconde signature, existence réelle, (puisqu'on reste dans le réel, et dans la même métrique), et égalité dans R, soit l’égalité des deux expressions : a^2 et – a^2 !!

Le fait que mach3 prétend pouvoir se passer de la notation imaginaire (son #55 à l’appui de l’affirmation maintes fois répétée dans le débat, qui le précise sans ambiguïté pour les temps (et déplacements) élémentaires :

Mais ds^2, dt^2 et dr^2 ne sont pas des réels, et encore moins des imaginaires. Ce ne sont pas des scalaires. Ce sont des tenseurs, des applications bilineaires qui transforment un couple de vecteur en un nombre réel.
Et ds, dt, dr ne sont pas non plus des réels ou des imaginaires. Ce ne sont pas des scalaires non plus. Ce sont des formes linéaires, qui transforment un vecteur en nombre réel.

m@ch3

montre qu’il doit pouvoir écrire : -1 = 1
Et donc utiliser :
moinsun.JPG
Cela se passe de commentaire !

Passant à l’écriture correcte de ces deux expressions, on obtient évidemment respectivement a^2 et ia^ia.

Et on constate évidemment que la seconde exige l’utilisation des nombres complexes, ce qui traduit le fait que la mathématique à l’intérieur du rayon de Schwarzschild est imaginaire et l’espace-temps lui-même imaginaire, ce à quoi avait conclu Karl de façon différente et beaucoup plus élégante.

[Archi3]

On en déduit donc que l’écriture de ce carré scalaire dans la première signature ( carré scalaire foncièrement réel en tant que carré d’une durée réelle, que l’on peut écrire [a^2]) donne donc, à l’opposé du carré de cette durée, que l’on écrira donc [– a^2], et via la seconde signature, existence réelle, (puisqu'on reste dans le réel, et dans la même métrique), et égalité dans R, soit l’égalité des deux expressions : a^2 et – a^2 !!

il y a combien de gens ici qui comprennent ce qu'écrit Bernarddo et si il y en a, ils pourraient me l'expliquer SVP ?

[Deedee81]

Salut,

il y a combien de gens ici qui comprennent ce qu'écrit Bernarddo et si il y en a, ils pourraient me l'expliquer SVP ?

Pas seulement le passage cité. Bernarddo, tu dois être fatigué, la moitié de tes phrases sont incompréhensibles.

[Archi3]

en fait je n'ai pas réussi à trouver le COD de "donne donc ..." , c'est même pas du français....

[Deedee81]

en fait je n'ai pas réussi à trouver le COD de "donne donc ..." , c'est même pas du français....

Manque juste la virgule..... mais ça n'aide pas.

[bernarddo]

en fait je n'ai pas réussi à trouver le COD de "donne donc ..." , c'est même pas du français....

Attention, tu vas encore te faire reprendre par mach3, le "donne" était repris de sa citation !!

[ordage]

Il n’y a aucune raison sauf, en situation difficile, à lancer une diversion bienvenue, de revenir à un cours d’algèbre tensorielle,.

Bonjour
Comme les tenseurs sont omniprésents en relativité (en particulier en relativité générale qui définit un champ gravitationnel de type tensoriel ), c'est mieux de comprendre ce qu'est un tenseur pour comprendre la théorie.
C'est aussi vrai (mais plus simple) en relativité restreinte, du moins dans l'approche "moderne" (à partir de Minkowski-1907) où l'espace-temps est le concept physique fondamental réduisant l'espace et le temps à n'en être que des ombres (dixit Minkowski).
Toutes les approches avec les transformations e Lorentz relèvent de la préhistoire de la relativité, où on a cherché désespérément à conserver les notions de temps et d'espace "newtoniens" en introduisant les notions de synchronisation par exemple qui montrent leurs limites. Mais il faut se rappeler qu'on ne peut pas dater de façon universelle un évènement, (la synchronisation universelle n'existe pas) et on n'en a pas besoin en relativité.
Cordialement

[Deedee81]

Attention, tu vas encore te faire reprendre par mach3, le "donne" était repris de sa citation !!

C'est pas ça le problème en fait.

[bernarddo]

Manque juste la virgule..... mais ça n'aide pas.

Pour quelqu'un qui se joint au concert des non "comprenants", je trouve ta lecture suffisamment attentive pour avoir pointé l'absence regrettable de la virgule, (qui était la seule chose pouvant rendre un peu difficile la compréhension du texte), pour ne pas croire une seconde que tu n'as pas parfaitement compris le texte, au moins sur la forme!

Sur le fond, si celui-ci avait été vraiment incompréhensible, c'est que quelque chose aurait cloché dans l'argumentaire, et une lecture aussi attentive d'un aréopage de matheux qui avaient parfaitement compris et intégré la "propriété fondamentale" de mach3, n'aurait pas manqué de trouver ce qui rendait incompréhensible un texte qui ne faisait qu'illustrer cette propriété fondamentale en rendant visibles les deux écritures équivalentes d'une même entité, (le carré de la durée propre), rendues possibles par cette propriété, et de tirer les conséquences de leur équivalence.

Permets-moi donc de faire le tour de ce qui pourrait constituer des impossibilités de compréhension sur le fond:

- une contestation sur le fait que mach3 revendique sans ambiguïté les deux écritures en nombres réels (citation): personne ne le revendique
- une erreur sur les deux écritures donc limitées ici à leur formulation en en nombres réels: personne ne le revendique
- le fait que l'on ne pourrait pas écrire l'identité de 2 formulations mathématiques d'une même entité sous forme d'équation: personne ne le revendique
- la constatation que les deux formulations en nombre réels ne peuvent être valables simultanément qu'en violation des règles mathématiques : personne ne le revendique
- la constatation du fait que cette identité n'est pas possible si les deux formulations sont exprimées en nombres réels: personne ne le revendique

- je laisse rajouter toutes contestations ultérieures sur ces points ou sur tous autres qui ne me viennent pas à l'esprit

Rien ne vient donc corroborer (sauf argument ultérieur recevable) la qualification d'"incompréhensible" de mon argumentaire, et je la reçois comme un procédé intellectuellement déloyal de la part de contradicteurs démunis d'arguments effectifs à l'appui de leur thèse.

La discussion reste ouverte...

[Deedee81]

[...] que tu n'as pas parfaitement compris le texte, au moins sur la forme!

C'est fou ce que ça aide
(comprendre la forme est indispensable mais plus qu'insuffisant)

Sur le fond, si celui-ci avait été vraiment incompréhensible, c'est que quelque chose aurait cloché dans l'argumentaire

Non, pas l'argumentaire. C'est juste tellement mal écrit que c'est incompréhensible. Un assemblage grammaticalement correct de mots mis n'importe comment. J'ai supposé que tu étais fatigué. Ca arrive.

Là dans le reste du message tu as en effet commis des erreurs de raisonnement (cette fois tu as écrit clairement ), mais outre que ça viole le point 6, cela a été dit plusieurs fois et rien ne sert de répéter ad nauseam. Tu ne comprends pas et ça ne changeras probablement pas sur un forum, enfin, bon, j'en doute c'est tout. Sans compter le "intellectuellement déloyal". Dire "c'est incompréhensible" n'est pas insultant, mais ça c'est une insulte (*) : sanction proche, très proche et vacances à la clef.
EDIT (*) constat sur un message v.s. juger les personnes ou leurs intentions

[Archi3]

Bonjour
Comme les tenseurs sont omniprésents en relativité (en particulier en relativité générale qui définit un champ gravitationnel de type tensoriel ), c'est mieux de comprendre ce qu'est un tenseur pour comprendre la théorie.
C'est aussi vrai (mais plus simple) en relativité restreinte, du moins dans l'approche "moderne" (à partir de Minkowski-1907) où l'espace-temps est le concept physique fondamental réduisant l'espace et le temps à n'en être que des ombres (dixit Minkowski).
Toutes les approches avec les transformations e Lorentz relèvent de la préhistoire de la relativité, où on a cherché désespérément à conserver les notions de temps et d'espace "newtoniens" en introduisant les notions de synchronisation par exemple qui montrent leurs limites. Mais il faut se rappeler qu'on ne peut pas dater de façon universelle un évènement, (la synchronisation universelle n'existe pas) et on n'en a pas besoin en relativité.
Cordialement

mouais, comment tu définis et mesures une vitesse, sans avoir un référentiel et un temps synchronisé ?

[Archi3]

Pour quelqu'un qui se joint au concert des non "comprenants", je trouve ta lecture suffisamment attentive pour avoir pointé l'absence regrettable de la virgule, (qui était la seule chose pouvant rendre un peu difficile la compréhension du texte), pour ne pas croire une seconde que tu n'as pas parfaitement compris le texte, au moins sur la forme!

Sur le fond, si celui-ci avait été vraiment incompréhensible,.

je veux bien admettre que ce que tu dis est tout à fait compréhensible et que l'incompréhension ne vienne que de mes capacités limitées, mais c'est pour ça que je demandais qui le comprenait. Pour le moment ça ne se bouscule pas au portillon . Donc au moins on pourrait te reprocher un manque de clarté dans l'expression au mieux, et au pire, de raconter n'importe quoi.

De quelles "deux écritures" tu parles ? On fait le choix d'une des deux signatures ou de l'autre, mais on ne mélange pas les deux !

[mach3]

mouais, comment tu définis et mesures une vitesse, sans avoir un référentiel et un temps synchronisé ?

Sans référentiel, on peut définir la vitesse relative entre deux corps par le produit scalaire entre leurs deux 4-vitesses qui donnera le gamma, éventuellement après avoir transporté parallèlement l'une des deux suivant un chemin "convenablement" choisi (si l'espace-temps est courbe). Le "convenablement" dépendra de la méthode de mesure. Par exemple, si c'est du Doppler, c'est le transport parallèle le long d'une géodésique nulle qui convient.

Nota : il est particulièrement éclairant de voir comment Adler résout le problème (dans la réponse à mach 3) :
On peut voir simplement sur la position attribuée aux exponentielles dans la métrique son refus d’entériner le changement de signe du second membre en niant celui des exponentielles. (page 187 du manuel)

Pièce jointe 454669

Le constat est cruel, Adler raterait son bac math élèm

Concernant Adler, il n'est pas facile de juger sur des extraits parcellaires.
A priori, ne peut pas être définie si r<2m, car elle requerrait alors que soit imaginaire pur EDIT : non, pas un imaginaire, mais un complexe dont la partie imaginaire vaut (en tant que logarithme népérien d'un nombre négatif). Du coup l'expression donnée pour la métrique, avec et son inverse dans les coefficient gtt et grr, ne devra pas être définie pour r<2m.
Après cela dépend de comment Adler l'utilise et ce qu'il en fait, ce que seul les possesseurs de ce livre peuvent savoir...
Cela étant dit, tant que gtt et grr restent des réels (ce qui est le cas même si est imaginaire pur!EDIT : non, un complexe dont la partie imaginaire est ), il ne pourra jamais sortir autre chose que des valeurs réelles (positive, négative ou nulle) lorsqu'on appliquera la métrique sur un couple de vecteur. Donc la manip reste "légale", réel signifiant simplement r>2m et imaginaire pur EDIT : non, pas un imaginaire, mais un complexe dont la partie imaginaire vaut ( signifiant simplement r<2m.
Tout ceci ressemble plus à un raccourci vers un résultat qui peut très bien être atteint sans faire usage d'un imaginaire en suivant un chemin plus long, un peu à la manière de ce qui se fait en électronique où en considérant des tensions et intensités complexes on simplifie drastiquement des calculs qu'on pourrait très bien faire sans jamais utiliser d'imaginaires.

Mais bon, tout cela nous fait une belle jambe, car quelque part ce que fait Adler dans son bouquin, on en a à peu près rien à faire vu que n'importe qui étudiant assez loin la relativité générale (que ce soit à la fac ou en autodidacte) sera capable démontrer par lui même l'expression de la métrique de Schwarzschild et d'exploiter cette expression sans jamais y faire apparaitre le moindre nombre imaginaire.

Arrêtons là sur Adler.


Il semble que le problème remonte peut-être plus loin, parce que la métrique de Minkowski elle-même n'est peut-être pas comprise. Petit test :

On considère un système de coordonnées de Lorentz t,x,y,z en espace-temps plat, tels que c=1. On considère deux évènements dont les coordonnées diffèrent de ,,,

1) Si on écrit , cette expression sera de signe positif, négatif ou nulle selon que l'intervalle entre les deux évènements et de genre temps, espace ou nul. OK ou pas OK ?

2) Si on effectue une transformation de Lorentz du système t,x,y,z vers un autre t',x',y',z', on a : . OK ou pas OK ?

3) Si l'expression est de signe positif (on a du genre temps), alors il existe une transformation de Lorentz de t,x,y,z vers de nouvelles coordonnées t',x',y',z' tel que , , soit nuls (les deux évènements se produisent au mêmes abscisse, ordonnée et cote). OK ou pas OK ?

4) Ainsi . OK ou pas OK ?

5) L'expression s'interprète alors comme le carré de la durée , durée propre entre les deux évènements. OK ou pas OK ?

6) Si l'expression est de signe négatif (on a du genre espace), alors il existe une transformation de Lorentz de t,x,y,z vers de nouvelles coordonnées t',x',y',z' (différentes des précédentes) tel que , , soit nuls (les évènements se produisent aux mêmes date, ordonnée et cote). OK ou pas OK ?

7) Ainsi . OK ou pas OK ?

8) L'expression s'interprète alors comme l'opposé du carré de la longueur , longueur propre entre les deux évènements. OK ou pas OK ?

Merci de répondre OK ou pas OK pour chaque proposition.

m@ch3

[ordage]

mouais, comment tu définis et mesures une vitesse, sans avoir un référentiel et un temps synchronisé ?

Bonjour
Oublie les les référentiels "synchronisés" , c'est un vestige de la mécanique newtonienne.
Mach3 a répondu à la question.
En relativité on utilise une 4-vitesse qui est un 4-vecteur.
Pour comparer deux 4 vecteurs il faut faire un "transport parallèle". En RR, pas de problème c'est un espace plat le résultat ne dépend pas du chemin suivi par le transport.
En RG le résultat dépend du chemin suivi.
En général, on résume cela en disant que parler de la vitesse d'un objet lointain en RG (espace-temps courbe) est "mathématiquement" un "non sens"".
En astrophysique, on estime la "vitesse" radiale d'un objet lumineux par le décalage spectral (un photon, issu de la source, mesuré dans le référentiel de l'observateur, sur une géodésique nulle dans l'espace-temps, ). Mais ce décalage peut résulter de différents effets (Doppler - cosmologique- gravitationnel) qui se composent. Reste à interpréter correctement la mesure.
Cordialement

[Archi3]

Bonjour
Oublie les les référentiels "synchronisés" , c'est un vestige de la mécanique newtonienne.
Mach3 a répondu à la question.
En relativité on utilise une 4-vitesse qui est un 4-vecteur.

OK mais il n'en reste pas moins que la vitesse "ordinaire" est liée à des composante du 4-vecteur donc dépend du référentiel - Mach 3 propose de mesurer la "vitesse relative" , je suis aussi d'accord, mais c'est une manière d'exprimer "la vitesse de A dans un référentiel lié à B" même si on l'exprime autrement.

Et quand il s'agit de faire des mesures concrètes de vitesse, l'emploi d'horloges bien synchronisées est indispensable, on l'a constaté avec l'affaire des neutrinos superluminiques .

Je comprends l'attrait intellectuel de concevoir la Relativité en fonction d'objets tensoriels intrinsèques sans parler de référentiel, mais je ne suis pas sûr que ça aide à comprendre ceux qui font des erreurs de représentation (le plus souvent en oubliant le caractère relatif de la simultanéité) de leur dire d'abandonner les référentiels ... parce que les mesures d'expériences concrètes, elles sont faites avec des étalons de mesure d'espace et de temps, et dans des référentiels. Je ne sais pas mesurer une 4-vitesse sans mesurer une vitesse ou une énergie dans un référentiel particulier moi.

[bernarddo]

Concernant Adler, il n'est pas facile de juger sur des extraits parcellaires.
A priori, ne peut pas être définie si r<2m, car elle requerrait alors que soit imaginaire pur (en tant que logarithme népérien d'un nombre négatif). Du coup l'expression donnée pour la métrique, avec et son inverse dans les coefficient gtt et grr, ne devra pas être définie pour r<2m.
Après cela dépend...

m@ch3

C’est tout vu et j’avais déjà montré l’extrait :



Adler considère tout simplement que ses exponentielles restent définies, les coefficients peuvent changer de signe ce qui valide le discours d’A Barrau. Cela introduit quand même sans le dire les imaginaires dans la boucle (pour λ et ν comme tu as pu le constater).

Personnellement, je partage ton excellente (et élémentaire) analyse mathématique de la situation pour r < 2m et en déduis (ce qui est cohérent avec la métrique (complète) de Sch) que, la métrique perdant son expression mathématique en termes réels, nous ne sommes plus dans un espace-temps réel où durées, trajectoires et temps propres doivent être réels simultanément.

[Archi3]

Personnellement, je partage ton excellente (et élémentaire) analyse mathématique de la situation pour r < 2m et en déduis (ce qui est cohérent avec la métrique (complète) de Sch) que, la métrique perdant son expression mathématique en termes réels,.

je ne vois pas ce qui te permet de dire que la métrique "perd son expression mathématique en termes réels", les coefficients de la métrique restent réels même si ils changent de signe.

[mach3]

je ne vois pas ce qui te permet de dire que la métrique "perd son expression mathématique en termes réels", les coefficients de la métrique restent réels même si ils changent de signe.

Sentiment partagé.

Et sinon, ce serait bien que Bernarddo réponde au test, auquel on peut ajouter les questions subsidiaires suivantes :

1-bis) Si on écrit , cette expression sera de signe positif, négatif ou nulle selon que l'intervalle entre les deux évènements et de genre espace, temps ou nul. OK ou pas OK ?

2-bis) Si on effectue une transformation de Lorentz du système t,x,y,z vers un autre t',x',y',z', on a : . OK ou pas OK ?

3-bis) Si l'expression est de signe négatif (on a du genre temps), alors il existe une transformation de Lorentz de t,x,y,z vers de nouvelles coordonnées t',x',y',z' tel que , , soit nuls (les deux évènements se produisent au mêmes abscisse, ordonnée et cote). OK ou pas OK ?

4-bis) Ainsi . OK ou pas OK ?

5-bis) L'expression s'interprète alors comme l'opposé du carré de la durée , durée propre entre les deux évènements. OK ou pas OK ?

6-bis) Si l'expression est de signe positif (on a du genre espace), alors il existe une transformation de Lorentz de t,x,y,z vers de nouvelles coordonnées t',x',y',z' (différentes des précédentes) tel que , , soit nuls (les évènements se produisent aux mêmes date, ordonnée et cote). OK ou pas OK ?

7-bis) Ainsi . OK ou pas OK ?

8-bis) L'expression s'interprète alors comme le carré de la longueur , longueur propre entre les deux évènements. OK ou pas OK ?

m@ch3

[stefjm]

Et là, j'ai comme l'impression qu'il faudrait accepter qu'on puisse écrire:

(-a)^1/2 * (-a)^1/2 = [(-a)^1/2]^2 = (-a)^1 = - a (définition qui malheureusement ne respecte pas le résultat correct: a

J'ouvre un concours pour en trouver une définition mathématiquement correcte qui n'aurait pas recours aux imaginaires

Facile et déjà fait!

https://fr.wikipedia.org/wiki/Racine...ation_continue

https://fr.wikipedia.org/wiki/Fonction_multivalu%C3%A9e

[bernarddo]

je ne vois pas ce qui te permet de dire que la métrique "perd son expression mathématique en termes réels", les coefficients de la métrique restent réels même si ils changent de signe.

C’est très simple, as-tu lu attentivement le # 79 ; C’est mach3 lui-même qui l’affirme !

A priori, ne peut pas être définie si r<2m, car elle requerrait alors que soit imaginaire pur (en tant que logarithme népérien d'un nombre négatif). Du coup l'expression donnée pour la métrique, avec et son inverse dans les coefficient gtt et grr, ne devra pas être définie pour r<2m.

Par chance, ta question m’a conduit à relire la suite de son message auquel je n’avais pas prêté suffisamment d’attention, et d’y découvrir une autre entorse aux mathématique qui, me semble-t-il, porte encore mieux notre désaccord en ma faveur et semble contredire son argumentaire quant à sa "légalité". (quel terme bizarre en mathématiques !)

Cela étant dit, tant que gtt et grr restent des réels (ce qui est le cas même si est imaginaire pur!), il ne pourra jamais sortir autre chose que des valeurs réelles (positive, négative ou nulle) lorsqu'on appliquera la métrique sur un couple de vecteur. Donc la manip reste "légale", réel signifiant simplement r>2m et imaginaire pur signifiant simplement r<2m.

Se pourrait-il que mach3 ignore la formule d’Euler, que je rappelle ici (pour les suiveurs muets, au cas où) :

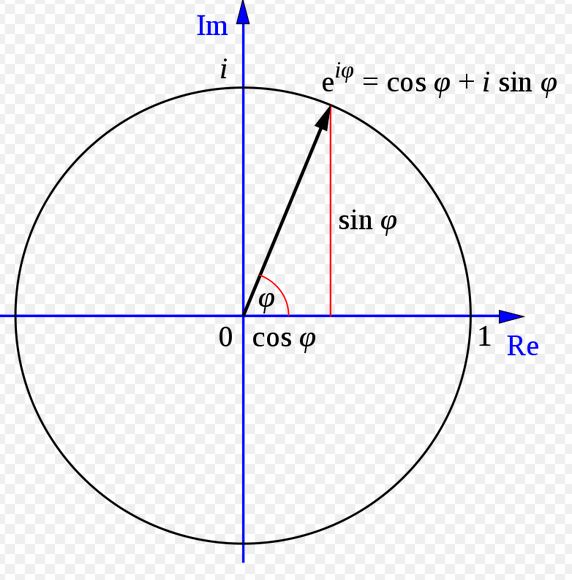
et qui s’applique donc ici à λ et ν pour r < 2m

Il en résulte que les valeurs réelles positives revendiquées par mach3 ne peuvent l’être que sur un plan complexe (qui n’est qu’un plan de représentation), mais en aucune façon dans le cadre de la métrique qui s’inscrit dans un cadre de coordonnées réelles.

Je peux bien sûr me tromper, mais c'est maintenant à mach3 de s’expliquer sur le sujet.

[Archi3]

C’est très simple, as-tu lu attentivement le # 79 ; C’est mach3 lui-même qui l’affirme !



Par chance, ta question m’a conduit à relire la suite de son message auquel je n’avais pas prêté suffisamment d’attention, et d’y découvrir une autre entorse aux mathématique qui, me semble-t-il, porte encore mieux notre désaccord en ma faveur et semble contredire son argumentaire quant à sa "légalité". (quel terme bizarre en mathématiques !)



Se pourrait-il que mach3 ignore la formule d’Euler, que je rappelle ici (pour les suiveurs muets, au cas où) :
Pièce jointe 454957
et qui s’applique donc ici à λ et ν pour r < 2m

Il en résulte que les valeurs réelles positives revendiquées par mach3 ne peuvent l’être que sur un plan complexe (qui n’est qu’un plan de représentation), mais en aucune façon dans le cadre de la métrique qui s’inscrit dans un cadre de coordonnées réelles.

Je peux bien sûr me tromper, mais c'est maintenant à mach3 de s’expliquer sur le sujet.

évidemment si tu paramètrises un nombre réel par ça peut te conduire à des valeurs de complexes, mais la métrique reste réelle ! on t'a déjà fait remarquer que les complexes apparaissaient souvent comme intermédiaire mathématique (dans tous les phénomènes vibratoires, la mécanique quantique etc ...), ça ne les empêchent pas de décrire le monde réel. Tu te fais des noeuds dans le cerveau pour rien.

[ordage]

mouais, comment tu définis et mesures une vitesse, sans avoir un référentiel et un temps synchronisé ?

Bonjour
La 4-vitesse relativiste n'est pas relative à un référentiel: elle est intrinsèque. Si tu considère la ligne d'univers (une courbe) d'une particule, par exemple, qui est définie dans l'espace-temps, sa 4-vitesse en un point c'est la tangente à la courbe en ce point (le 4-vecteur tangent). Son module (auto-produit scalaire) est constant (c²). Elle n'est pas définie par rapport à un référentiel. Tu peux évaluer cette 4-vitesse sur une autre ligne d'univers, par projection des composantes du 4-vecteur transporté parallèlement au point de projection. L'expérience dont tu parles, c'est une expérience de type Newtonien parfaitement adapté au problème à traiter. Quand on parle de 3-vitesse, on est en approche newtonienne ou pseudo-newtonienne. Ce n'est pas une critique de ce type d'approche, mais en général, pour un pb de relativité, c'est plus clair et en général plus simple, d'utiliser le formalisme relativiste.
Cordialement

[Archi3]

QUOTE=Archi3;6913406]mouais, comment tu définis et mesures une vitesse, sans avoir un référentiel et un temps synchronisé ?

Bonjour
La 4-vitesse relativiste n'est pas relative à un référentiel: elle est intrinsèque.

non je te parle de 3 vitesse normale dOM/dt

Ce n'est pas parce que ce sont des composantes de 4-vecteurs (donc dépendant du référentiel) que ça "n'existe pas", et ce n'est pas seulement "newtonien" (cf formule de composition des vitesses). Par exemple dire que la vitesse de la lumière est toujours égale à c, c'est tout à fait relativiste , et ça parle bien de la vitesse "habituelle" dOM/dt .

[mach3]

Se pourrait-il que mach3 ignore la formule d’Euler, que je rappelle ici (pour les suiveurs muets, au cas où) :

Bourde monumentale qui mérite les plus plates excuses. Il ne s'agit pas d'une valeur imaginaire pure pour lambda, car elle donnerait des coefficients gtt et grr complexes ! Il s'agit bien sûr d'une valeur complexe dont la partie imaginaire vaut pi, ce qui donne toujours des valeurs réelles pour gtt et grr.

Le message problèmatique sera annoté en ce sens. Merci d'avoir pointé l'erreur.

m@ch3