1S Tétraèdre et polynôme de degré deux
Bonjour à tous!
J'aurai besoin de votre aide pour un exercice "tétraèdre et polynôme de degré deux" dont voici l'énoncé :
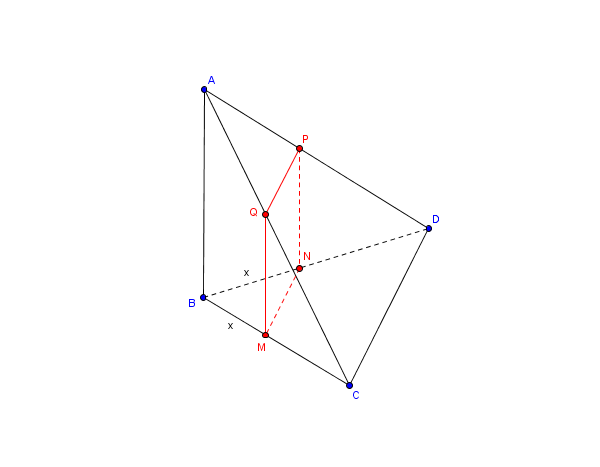
ABCD est un tétraèdre, BCD est un triangle équilatéral : BC = BD = CD = AB = 4 cm.
La droite (AB) est orthogonale au plan (BCD). M est un point variable sur le segment [BC]. On pose BM = x (en cm). Le plan passant par M et parallèle aux droites (AB) et (CD) coupe (BD) en N, (AD) en P et (AC) en Q. On suppose que M est différent de B et que M est différent de C.
1. Démontrer que le quadrilatère MNPQ est un parallélogramme.
2. Démontrer que les droites (QM) et (MN) sont perpendiculaires.
3. a) Exprimer MN en fonction de x.
b) Exprimer MQ en fonction de x.
c) Exprimer l'aire de MNPQ en fonction de x.
4. f est la fonction définie sur l'intervalle [0 ; 4] par : f (x) = 4 x - x²
a) Après avoir exprimer f sous forme canonique, étudier le sens de variation de f.
b) Dresser le tableua de variation de f.
c) Pour quelle positon de M sur [BC], l'aire de MNPQ est-elle maximale ? Que vaut alors cette aire ?
-----
