parabole et tangentes

[inviteb21e9a19]

boujour , alors voila j'ai une exercice sur les tangeantes avec une parabole et des fonctions et tous et tous , qui , il faut le dire , m'échappe mais totalement !

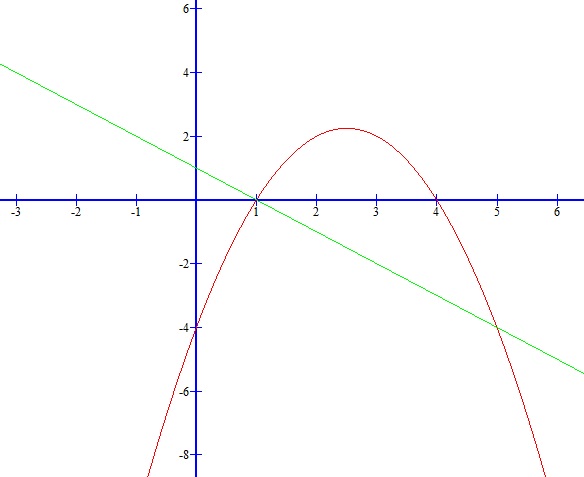
Alors voici le graphique :

Alors , soit la fonction f définie sur R par :

f(x)=-x²+5x-4
et P la parabole qui represente f dans une repère orthonormal

1)Dérerminer les points de P où la tangeante à P passe par 0 , l'origine du repère.

2)Montrer que la tangeante à P est parallèle a la droite d d'equation y=-x+1

Voila étant donné que je ne comprend rien du tout , enfin si je comprend mais je n'ai aucune méthode , je solicite votre aide , merci d'avance !
-----

[Jeanpaul]

Dans ton cours, tu as vu la formule qui donne l'équation de la tangente au point x=u d'une courbe y=f(x).
C'est le moment de t'en servir.

[Duke Alchemist]

Bonsoir.

... soit la fonction f définie sur R par :
f(x)=-x²+5x-4
et P la parabole qui represente f dans un repère orthonormal

1)Dérerminer les points de P où la tangeante à P passe par 0 , l'origine du repère.

Un rappel ici
Il te faut donc :
- déterminer la dérivée de la fonction
- appliquer la relation rappelée ci-dessus en un point d'abscisse a (sans préciser de valeur)
- développer l'expression de manière à avoir l'équation d'une droite y = m*x + p
- déterminer la(les) valeur(s) de a pour laquelle (lesquelles) les coordonnées (0;0) vérifient l'équation de la tangente à P.

2)Montrer que la tangeante à P est parallèle a la droite d d'equation y=-x+1

Il manque au point d'abscisse x=3, non ?
Si la tangente doit être parallèle à la droite donnée, que peux-tu dire de son coefficient directeur (ou sa pente, c'est pareil) ?

Duke.

[inviteb21e9a19]

Merci beaucoup Duke , donc pour le 1) j'ai compris , je n'avias pas cette formule (absent =S)
Ensuite pour le 2) Non on a pas x , mais je me suis débrouiller pour le trouver , avec la dérivée de f(x) et de y ^^

merci encore !!

[A voir en vidéo sur Futura]

[inviteb21e9a19]

Désolé du double post , mais quel valeur prendre pour a ?

Si je considere aucune valeur pour a , j'ai

f(a) = -a²+5a-4
f'(a)= -2a + 5
Et apres avoir suivit l'equation f'(a)(x-a) + f(a)
J'ai -2ax +a² +5x -4

Et je sais pas quoi faire avec ça , donc a ne doit pas etre egale a 0 vu que on demande a l'origine ?

[ansset]

Désolé du double post , mais quel valeur prendre pour a ?

Si je considere aucune valeur pour a , j'ai

f(a) = -a²+5a-4
f'(a)= -2a + 5
Et apres avoir suivit l'equation f'(a)(x-a) + f(a)
J'ai -2ax +a² +5x -4

Et je sais pas quoi faire avec ça , donc a ne doit pas etre egale a 0 vu que on demande a l'origine ?

justement , on te demande de chercher les "bonnes" valeur de a.
tu as bien ecrit l'équation des tangentes.
mais on te propose de trouver celles qui passent par le point (0,0) soit celles qui sont valables pour x=0
et tu trouveras les bonnes valeurs de a .

[inviteb21e9a19]

Donc je doit avoir x=0 mais dans quel équation ? Dans f'(a)(x-a)+f(a) ?

[ansset]

Donc je doit avoir x=0 mais dans quel équation ? Dans f'(a)(x-a)+f(a) ?

OUI dans celle que tu viens de donner qui dépendait de a et de x..
fonction qui d'ailleurs doit valoir 0 puisque la tangente passe par (0,0)

[Duke Alchemist]

Re-

Je n'ai pas revérifié les calculs
mais si tu as y = -2ax +a² +5x -4 qui peut être écrit y = (5-2a)x + a²-4 (c'est mieux pour une équation de droite) et que cette droite doit passer par l'origine, alors tu dois résoudre y = (5-2a)x + a²-4 avec x = 0 et y = 0.
Tu auras ainsi les valeurs de a.

Pour le suivant, tu dois trouver a telle que la pente de la tangente soit égale à -1.

Duke.

[inviteb21e9a19]

Donc , si vous le permettez je vais faire les caluls ici , pour ne pas etre trop perdu

x=0

Donc
y= f'(a)(x-a)+f(a)
y=(-2a+5)(-a)+(-a²+5a-4)
y=2a²-5a-a²+5a-4
y=a²-4

soit

y=mx+p
comme x=0
y=p
a²-4=p

c'est ça ou non ? parce que je sais plus trop quoi faire ensuite =S

[ansset]

mais y aussi vaut 0 puisque la tangente passe par (0,0 )
donc a = ..... ou = ......

[inviteb21e9a19]

Désolé j'ai voulu éditer mais trop tard ,


Donc oui , comme y=0 , alors
a²-4=0
a=2 ou a=-2 non ? c'est ça ?

Oui je pense que c'est ça , merci beaucoup a vous tous , =D merci !

[inviteb21e9a19]

Enfin il me reste a calculer la pente m n'est-ce pas ?

m=yb-ya/xb-xa
= 0-2/0-(-2) = -1

C'est ça?

[inviteb21e9a19]

Enfin il me reste a calculer la pente m n'est-ce pas ?

m=yb-ya/xb-xa
= 0-2/0-(-2) = -1

C'est ça?

Désolé pour le multi post , mais non en fait je doit just faire f(2) et f(-2) pour avoir y et c'est tous.

[Duke Alchemist]

Re-

OK pour la première partie, on a bien a = ±2.

Enfin il me reste a calculer la pente m n'est-ce pas ?

m=yb-ya/xb-xa
= 0-2/0-(-2) = -1

C'est ça?

Euh... mais à quoi te sert le calcul de la dérivée et l'équation de la tangente alors ?

y = (5-2a)x + a²-4
avec la pente 5-2a = -1 donc a = ...

Duke.