Bonjour à tous,
Un problème me rend la tâche compliqué !
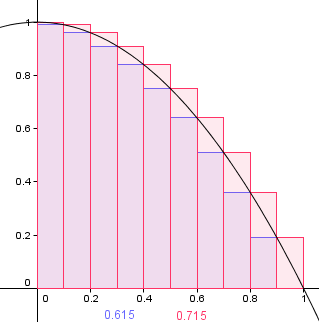
On considère la fonction f définie sur R par f(x) = 1 - x^2 e Cf sa coure représentative dans un repère orthonormal. Le but est de déterminer la valeur de l'aire de la partie du plan délimitée par l'axe des abscisses, la courbe Cf et les droites d'équation x=0 et x=1. On divise le segment (0;1) en n segments. On note A(n) l'aire recherchée.
L'aire A(n) cherchée est comprise entre l'aire Un, somme des aires des rectangles inférieurs et l'aire Vn qui est la somme des aires des rectangles inférieurs.
Questions
1) J'ai montré par récurrence que 1^2+2^2+3^2+4^2+...+n^2 = (n(n+1)(2n+1))/6 pas besoin d'y revenir
2) Determiner Vn en fonction de n (rectangles supérieurs)
3) Donner un encadrement de A(n) en fonction de n
Il reste 3 questions par la suite que je suis incapable de resoudre sans les questions 2) et 3). Elles me débloqueraient le problème !
Merci de votre aide
-----