Simplification d'une somme

**Theos59** · 08/09/2013, 13h29

Bonjour,
Je n'arrive pas à simplifier cette somme : Sigma pour k=o jusque k=n de (exp(k*x)+exp(-k*x))/2
Si je pouvais avoir juste un indice pour démarrer ce serait super !
Merci !

**Theos59** · 08/09/2013, 13h51

Voici ce que ça donne correctement écrit
. Nom : daum_equation_1378644566508.png
Affichages : 71
Taille : 2,4 Ko

**gg0** · 08/09/2013, 13h56

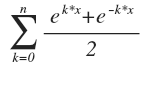
Bonjour.

Si tu connais la trigo hyperbolique, tu reconnais une somme de ch.

mais en développant ta somme, tu verras que c'est une somme de termes en progression géométrique :
$\text{[math]}$

Cordialement.

**Theos59** · 08/09/2013, 14h15

D'accord donc j'obtiens ça :
Nom : daum_equation2.png
Affichages : 73
Taille : 2,8 Ko

A voir en vidéo sur Futura · Aujourd'hui

**Theos59** · 08/09/2013, 14h41

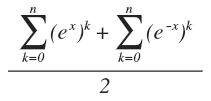
Et là plus rien ...

**gg0** · 08/09/2013, 14h43

Pour l'instant,

on ne peut pas lire ta pièce jointe (il faut qu'un administrateur la valide).
Et après tout, personne n'est tenu de te répondre ...

**Theos59** · 08/09/2013, 14h47

Quand je disais plus rien c'est juste que n'ai plus d'idées c'est tout et que j'y arrive pas. Déjà je demande de l'aide, je ne me permettrai pas ce genre de réflexion

**gg0** · 08/09/2013, 14h53

Ah ! Ok !

Comme quoi, faire des phrases complètes évite d'être mal compris.

Alors regarde (développe) pour des petites valeurs de n, 2, 3 ou 4, en réordonnant les puissances.

Quand on a du mal avec les sommes, on les développe; quand on a un cas général, on peut regarder des cas particuliers. Les idées ne viennent pas sans raison.

Cordialement.

**Theos59** · 08/09/2013, 14h58

Ok merci je vais essayer ça !!

**Theos59** · 08/09/2013, 17h02

Même en développant je n'arrive pas à trouver une expression qui puisse regrouper tous les termes en une seule expression.

**gg0** · 08/09/2013, 17h07

En ne considérant que le numérateur et laissant 1 de côté, tu ne trouves pas une somme de puissance de e^x pour des exposants variant de -n à n ? C'est une série géométrique finie, qu'on sait écrire en une seule fraction.

**Theos59** · 08/09/2013, 17h18

Si j'ai bien compris je trouve ça :
Nom : daum_equation_1378657113060.png
Affichages : 72
Taille : 3,0 Ko

**Lucien-O.** · 08/09/2013, 19h10

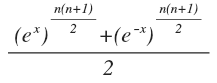
Salut, ma curiosité a été piquée et j'ai tenté de résoudre la question également, donc je m'immisce un brin car je n'aboutis pas à ta réponse Théos (mais je ne suis pas certain que ma réponse soit juste).

J'ai développé la somme et je l'ai traitée comme une suite géométrique d'origine $\text{[math]}$ et de raison $\text{[math]}$ .
Donc la somme des $\text{[math]}$ premiers termes, en laissant $\text{[math]}$ de coté et en mettant $\text{[math]}$ en évidence, doit valoir $\text{[math]}$ en considérant simplement la formule de la somme des termes d'une SG.

Est-ce correct?

**PlaneteF** · 08/09/2013, 19h50

Bonsoir,

Envoyé par Lucien-O.

J'ai développé la somme et je l'ai traitée comme une suite géométrique d'origine $\text{[math]}$ et de raison $\text{[math]}$ .
Donc la somme des $\text{[math]}$ premiers termes, en laissant $\text{[math]}$ de coté et en mettant $\text{[math]}$ en évidence, doit valoir $\text{[math]}$ en considérant simplement la formule de la somme des termes d'une SG.

Est-ce correct?

Dans la somme que tu considères il y a $\text{[math]}$ termes car tu ne laisses qu'un seul " $\text{[math]}$ " de côté, pas les deux, ... sinon il y aurait un "trou" dans la somme de termes d'une suite géométrique (tu ne peux pas passer de l'exposant -1 à +1 sans passer par 0).

Cordialement

**Lucien-O.** · 08/09/2013, 20h03

Bien sûr!
Voilà où le bât blessait, merci!

Bonne soirée.

**gg0** · 08/09/2013, 20h21

Effectivement,

la formule de Theos59 n'est pas la bonne.
Il y a cependant un cas particulier pour x=0, qui donne une valeur qui est la limite en 0 du cas général.

Cordialement.

**Theos59** · 14/09/2013, 15h16

Bonjour
J'ai fini par trouver le résultat final :
Nom : im.png
Affichages : 46
Taille : 5,1 Ko

Merci pour votre aide

TH59

Simplification d'une somme

Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Re : Simplification d'une somme

Discussions similaires

Simplification de somme

simplification de somme

Convergence et limite de la somme d'une somme [séries]

Simplification de polynome (somme récursive)

Déterminer le taux d'intérêt à partir de la somme investie et de la somme de fin de placement ?