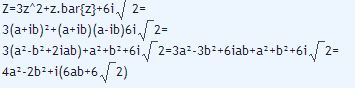Bonsoir a tous ,Voila j'ai exo que j'ai déjà bien entamer mais que n'arrive pas a terminer.Voici l'énoncé ,"Soit z=x+iy,x et y réels.Déterminer les parties réél et imaginaires de 3z²+z.z(barre)+6i2,En déduire les solutions de 3z²+z.z(barre)+6i2=0".
Pour ma part j'ai remplacer les z et z(barre) par (x+iy) et (x-iy) ,j'ai développer et réduit jusqu'à arriver à:
4x²+2y²+i(6xy+62)=0 <= Si quelqu'un pourrais vérifier si je n'ai pas fait d'erreur ça serais gentil.
Donc j'ai deux équations :
4x²+2y²=0 i(6xy-62)=0
x=2/y
Et c'est a la deuxieme équation que je bloque si quelqu'un peut me corriger et m'aider a le terminer ça serait sympas
-----