Démonstration en logarithme népérien

[invite2f157629]

Bonjour,

Comment peut on démontrer que lim_{x- 0} ln(x)/x=1 ?
-----

[invitec996fb1f]

vérifie ta limite il me semble que c'est 0

[inviteaf48d29f]

Alors qu'en fait ce n'est ni l'un ni l'autre.

Il serait intéressant de distinguer les cas suivant que x tend vers 0 par valeurs positive ou négative. Il y a de bonnes chances que la quantité ln(x)/x n'admette pas de limite sinon.

Je précise aussi qu'il ne faut pas écrire lim_{x-> 0} ln(x)/x=... avant d'avoir démontré que ln(x)/x admet effectivement une limite en 0. On ne peut pas se demander à quoi est égale une limite si on n'est même pas sûr que cette limite existe bel et bien.

[invitec996fb1f]

Je ne comprends pas

Il serait intéressant de distinguer les cas suivant que x tend vers 0 par valeurs positive ou négative.

il me semble que la fonction ln est définie pour des valeurs strictement positives donc chercher sa limite quand x tend vers 0 par valeur inférieur n'a pas de sens.
Cdt

[A voir en vidéo sur Futura]

[gg0]

Bonjour.

En écrivant

on trouve facilement la limite quand x tend vers 0 par valeurs supérieures, qui n'est ni 1, ni 0.

Cordialement.

NB : D'accord avec MoonRunner : Pas de limite à gauche.

[invite2f157629]

donc la limite de ln(x) tend vers 0 est 1 et 1/x est 0 donc 1x0=0

[PlaneteF]

donc la limite de ln(x) tend vers 0 est 1 et 1/x est 0 donc 1x0=0

Un peu de sérieux stp.

Cordialement

[invite51d17075]

Bonjour,

Comment peut on démontrer que lim_{x- 0} ln(x)/x=1 ?

tu es sur qu'on te demande la limité en 0+,
parce qu'en 0+, il n'y a même pas de calcul ou de demo à faire.?

[PlaneteF]

Bonjour ansset,

tu es sur qu'on te demande la limité en 0+,
parce qu'en 0+, il n'y a même pas de calcul ou de demo à faire.?

Je pense qu'avant que saoca puisse faire des démonstrations ou des caluls, il va falloir quand même "régler" ce genre de chose "surprenante" (et c'est un euphémisme) :

donc la limite de ln(x) tend vers 0 est 1 et 1/x est 0 donc 1x0=0

[invite51d17075]

confusion dans l'énoncé avec ln(1+x) ?

[inviteaf48d29f]

Ansset, visiblement il n'y a pas besoin que ce soit une forme indéterminée pour que tout le monde se plante sur cette question, il faut croire qu'elle est assez dure comme ça ^^.

[invite2f157629]

je n'est toujours pas compris comment trouver la limite ln(x)/x lorsque x tend vers 0.

[inviteaf48d29f]

Saoca, ce n'est pas une forme indéterminée. ln(x)/x peut aussi être vu comme le produit de ln(x) avec 1/x.

Vers quoi tend ln(x) quand x tend vers 0 ? Vers quoi tend 1/x quand x tend vers 0 (par valeurs positives) ?
Le produit de ces deux limites ?

[invite936c567e]

Bonsoir

Je pense que pour certains ici, un petit rappel sur la fonction logarithme s'impose :

[invite5756bcb3]

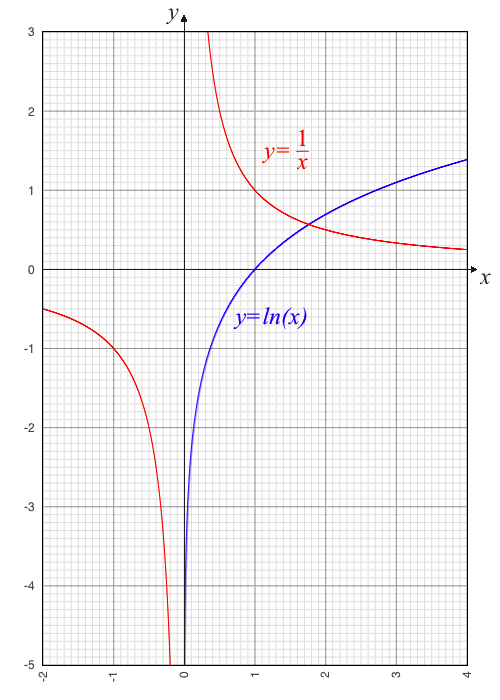
Le mieux est de dire les choses clairement il me semble...
ln(x) n'étant pas défini pour les valeurs négatives, la limite n'existe qu'à droite pour O+





n'est pas une forme indéterminée comme le serait + et donne

[invite936c567e]

Le mieux est de dire les choses clairement il me semble...

... mais pas de faire tout l'exercice à la place du demandeur.

[inviteaf48d29f]

Le mieux est de dire les choses clairement il me semble...

Au contraire. L'intérêt pédagogique de ce forum est d'aider les gens à réfléchir correctement à leurs problème de maths. Toi, Pa5scal et moi sommes capable de répondre à la question de Saoca, mais ce n'est pas nous qui sommes évalués. En lui donnant la réponse de manière à ce qu'il n'ait que besoin de la recopier sans réfléchir tu ne l'aide pas à comprendre, tu l'aides peut-être à avoir une bonne note et à faire illusion.
A cause de ce genre de remarque c'est possible que son prof ne se rende pas compte des difficultés de Saoca (qui sont visiblement assez importantes) et donc qu'il n'agisse pas en conséquence. Le problème c'est que le jour de ses examens tu ne seras plus là pour lui donner les réponses.

Donc non, le mieux est de s'abstenir de faire les exercices à la place de l'intervenant. Ça ne l'aide pas et ça gâche le travail pédagogique de ceux qui tentent de l'aider.

[invite5756bcb3]

Vous avez tout à fait raison. ça me semblait ici juste un peu confus dans la profusion de réponses fausses mélangées à des indications pertinentes ou non.

[invite51d17075]

Vous avez tout à fait raison. ça me semblait ici juste un peu confus dans la profusion de réponses fausses mélangées à des indications pertinentes ou non.

je n'ai vu que le mess #2 qui était faux.
cordialement.

[invite2f157629]

merci a tous j'ai compris, et encore merci.