Bonsoir PlaneteF.
A ce stade, quel pourcentage de ce qu'écrira Mllx est de toi ? 90% ?
En médecine, on appelle ça de l'acharnement thérapeutique
Cordialement.
-----

Bonsoir PlaneteF.
A ce stade, quel pourcentage de ce qu'écrira Mllx est de toi ? 90% ?
En médecine, on appelle ça de l'acharnement thérapeutique
Cordialement.

Dernière modification par PlaneteF ; 15/11/2014 à 19h50.

ben au moins Mllx s'accroche et ne cherche pas une solution toute prête, même s'il a parfois envoyé des mess un peu rapides : "pour voir".
accordons (lui/elle) cela.
pour le reste je suis tj admiratif devant la patience de PlaneteF.
cordialement à tous.

A vraie dire c'est grâce au personne qui m'aide sur ce forum qui fait que je l'accroche encore parce que j'avais commencer a laisser tomber l'année dernière (je n'avais même pas la moyenne au passage le fais de passe de 16 de moyenne a même pas 10 sur mes deux première années de lycée m'n fais un choc ) donc voilà , je suis peut être très lente a la détente mais je vous demanderais d'être très indulgent avec moi
Cordialement
D'ailleurs pour revenir au devoir je voudrais savoir si mon tableau de signe de g'(x) et la variation de g(x) est juste pour que je puisse commencer et terminer la dernière question
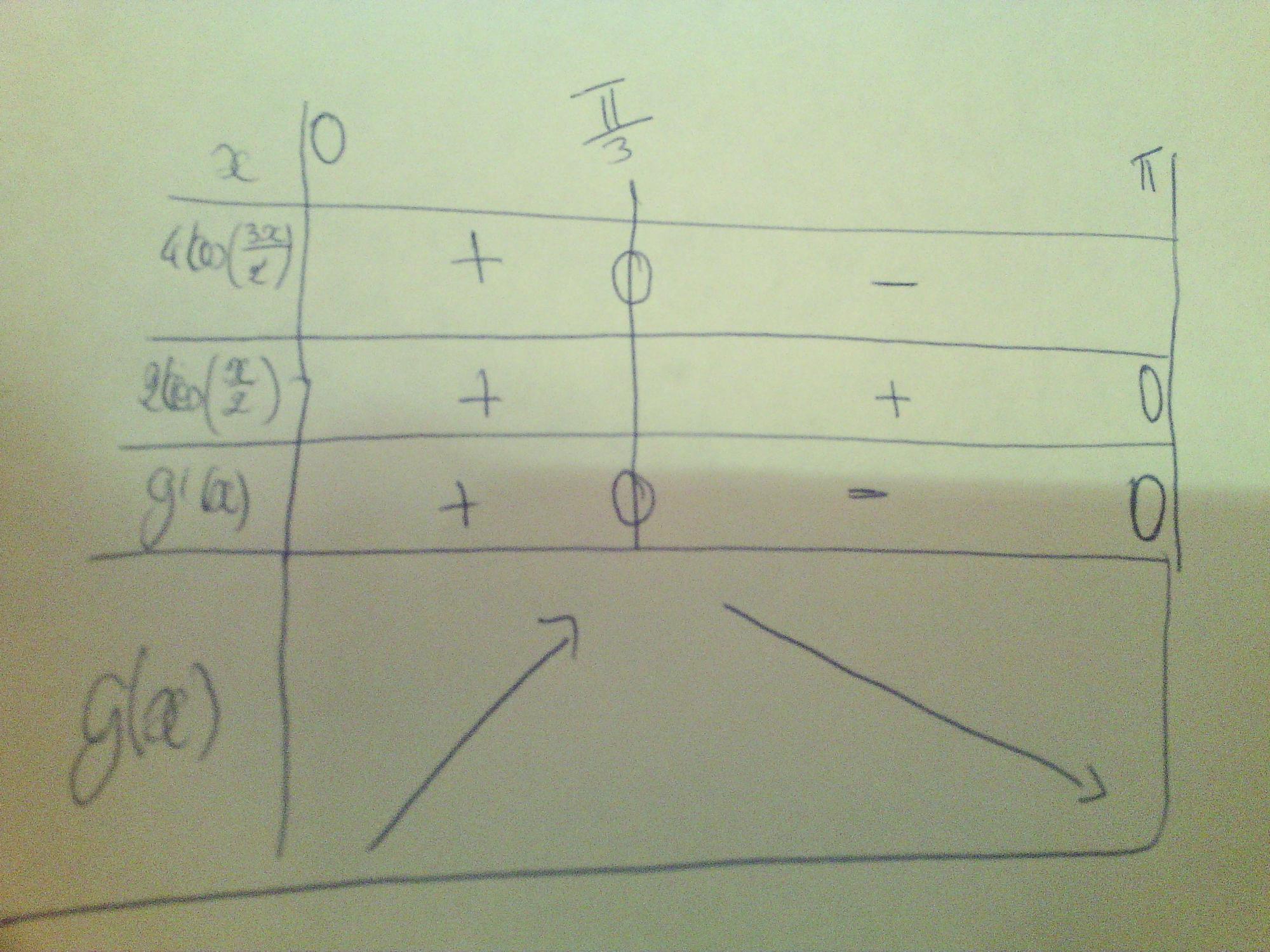

Tu as mis un facteurdans la 2e ligne du tableau, puis un facteur
dans la 3e, soit un facteur
pour
, ce qui n'est pas le cas.
Sinons'annule aussi en
Cdt
Dernière modification par PlaneteF ; 15/11/2014 à 20h48.

J'ai s'éparé la formule G'(x) en deux donc ça donne dans le tableau :
4cos(3x/2)
2cos(x/2)
j'ai pas mis en facteur on voit pas voir très bien .
g(π)=0
Et g(π/3)= une valeur approcher 2,..



Oui car c'est le signe deque l'on étudie, ... pas la fonction
elle-même.
Dernière modification par PlaneteF ; 15/11/2014 à 21h41.

OK d'accord ..
J'aurais une question pour la suite du devoir .. Dans la question 4 , on me demande de représenter la fonction g sur [-2π;2π]
C'est-à-dire une représentation graphique ?! C'est juste pour être sur ...

Oui ...
Cdt

OK d'accord , merci beaucoup pour votre aide , pour cette question vous ne pourrez pas donc je vais me débrouiller encore MERCI bonne fin de soiré
Cordialement .

tu es sure que c'est [-2π;2π] et pas [0;2π] ou [-π;π] ?
c'est un peu curieux vu la périodicité de g. ou alors c'est pour bien l'illustrer.
cordialement.

Salut ansset,
Là dessus je trouve l'énoncé plutôt cohérent, car sinon :
- Si l'on demande une représentation sur, tu ne peux pas le faire avec la seule étude sur
, sauf à y voir une symétrie par rapport au point
mais cela n'est pas demandé avant par l'énoncé. Et en plus on n'utiliserait pas la périodicité de la fonction qui est quand une de ses caractéristiques essentielles, ... donc ce serait ballot

- Si l'on demande une représentation sur, tu peux le faire en utilisant la parité de la fonction, ... mais même remarque au sujet de la périodicité non utilisée.
Par contre une représentation surfait utiliser et la parité et la périodicité de la fonction.
Cdt
Dernière modification par PlaneteF ; 16/11/2014 à 10h51.

... d'ailleurs en te relisant c'est peut-être ce que tu voulais dire par : " (...) ou alors c'est pour bien l'illustrer.".
Cdt
Dernière modification par PlaneteF ; 16/11/2014 à 11h03.

oui c'était ça.
phrase corrective que j'ai rajouté en me relisant.
Cdt.

