[aide] Etude d'une fonction trigonométrique

[invite6488a89f]

... donc quelle est la conclusion évidente quant au signe de , ... et quels sont les 2 cas à envisager pour étudier le signe de (tu peux t'aider d'un cerlce trigo si tu ne visualises pas ce qui se passe).

Cdt

Pour le signe de cos(x/2) : il est strictement positif ou nul en pi/2 et strictement négatif sur [ pi/2 ; pi ]
Et pour le signe de cos(3x/2) : il est strictement positif sur [ 0 ; pi/2] et strictement négatif sur [π/2 ; π ]
J'ai bienr répondu a votre question ?!
-----

[PlaneteF]

Pour le signe de cos(x/2) : il est strictement positif ou nul en pi/2 et strictement négatif sur [ pi/2 ; pi ]
Et pour le signe de cos(3x/2) : il est strictement positif sur [ 0 ; pi/2] et strictement négatif sur [π/2 ; π ]
J'ai bienr répondu a votre question ?!

Non, c'est faux.

[invite6488a89f]

Non, c'est faux.

Haha moi qui croyais avoir compris ...
Où est mon erreur ?!

[PlaneteF]

Un cosinus est positif sur --> Conclusion pour

Un cosinus est positif sur , et négatif sur --> Conclusion pour

[invite6488a89f]

Un cosinus est positif sur --> Conclusion pour

Un cosinus est positif sur , et négatif sur --> Conclusion pour

Bonjour,

> 0 <=> x E
< 0 <=> x E
=0 <=> x = pi//2


> 0 <=> x E
= 0 <=> x = [ pi/2]

ESt-ce sa ?

[PlaneteF]

Bonjour,

> 0 <=> x E
< 0 <=> x E
=0 <=> x = pi//2

> 0 <=> x E
= 0 <=> x = [ pi/2]

ESt-ce sa ?

Pas du tout.

Cdt

[invite6488a89f]

Bonjour,



Pas du tout.

Cdt

je dois étudier le signe de g'(x) sur [ 0 ; pi ] donc le signe de cos(3x/2) et positif sur [0 ; pi/2 ] et négatif sur [pi/2 ; 3pi/2 ] jusqu'à la j'ai bon ?

[PlaneteF]

Non c'est faux :

et positif sur [0 ; pi/2 ]

Positif pour , ... pas pour

négatif sur [pi/2 ; 3pi/2 ]

Idem

[invite6488a89f]

Non c'est faux :



Positif pour , ... pas pour




Idem

Donc
cos(3x/2) est positif sur [0;pi/2] <=> 3x/2 E [0;pi/2 ]
et est negatif lorsque 3x/2 E [ pi/2 ; pi ]
comme ça ?

[PlaneteF]

Mais la "variable" qui nous intéresse ce n'est pas , mais

[invite6488a89f]

Mais la "variable" qui nous intéresse ce n'est pas , mais

HA oui bas c'est sa que je comprend pas alors , comme en passe de 3x/2 à x ?

[PlaneteF]

Pour l'étude du signe de pour c'est-à-dire pour

1er cas :



Conclusion pour le signe de


2e cas :



Conclusion pour le signe de


Ensuite tu précises les endroits où s'annule

[invite6488a89f]

Pour l'étude du signe de pour c'est-à-dire pour

1er cas :



Conclusion pour le signe de


2e cas :



Conclusion pour le signe de


Ensuite tu précises les endroits où s'annule

pour le 1er cas :

[PlaneteF]

Ben oui, ...

[invite6488a89f]

pour le 1er cas :

pour le 2 eme cas :
pi/2 < 3x/2 <= 3pi/2
<=> pi/3 < x <= pi

[PlaneteF]

Ben oui, ... enchaîne, enchaîne ...

[invite6488a89f]

pour le 2 eme cas :
pi/2 < 3x/2 <= 3pi/2
<=> pi/3 < x <= pi

donc

cos(3x/2) est positif losque x E [0 ; pi /3 ]
et negatif


Non, en faite j'arrive pas à en déduire son signe malgré que j'ai fais un cercle trigonométrique sur une feuille

[invite6488a89f]

donc

cos(3x/2) est positif losque x E [0 ; pi /3 ]
et negatif


Non, en faite j'arrive pas à en déduire son signe malgré que j'ai fais un cercle trigonométrique sur une feuille

cos(3x/2) est positif sur [ 0 ; pi/3 ] et négatif sur [ pi/3 ; pi ]
oui / non ???

[PlaneteF]

Ben oui, ...

[invite6488a89f]

Ben oui, ...

ha ouf enfin :
donc
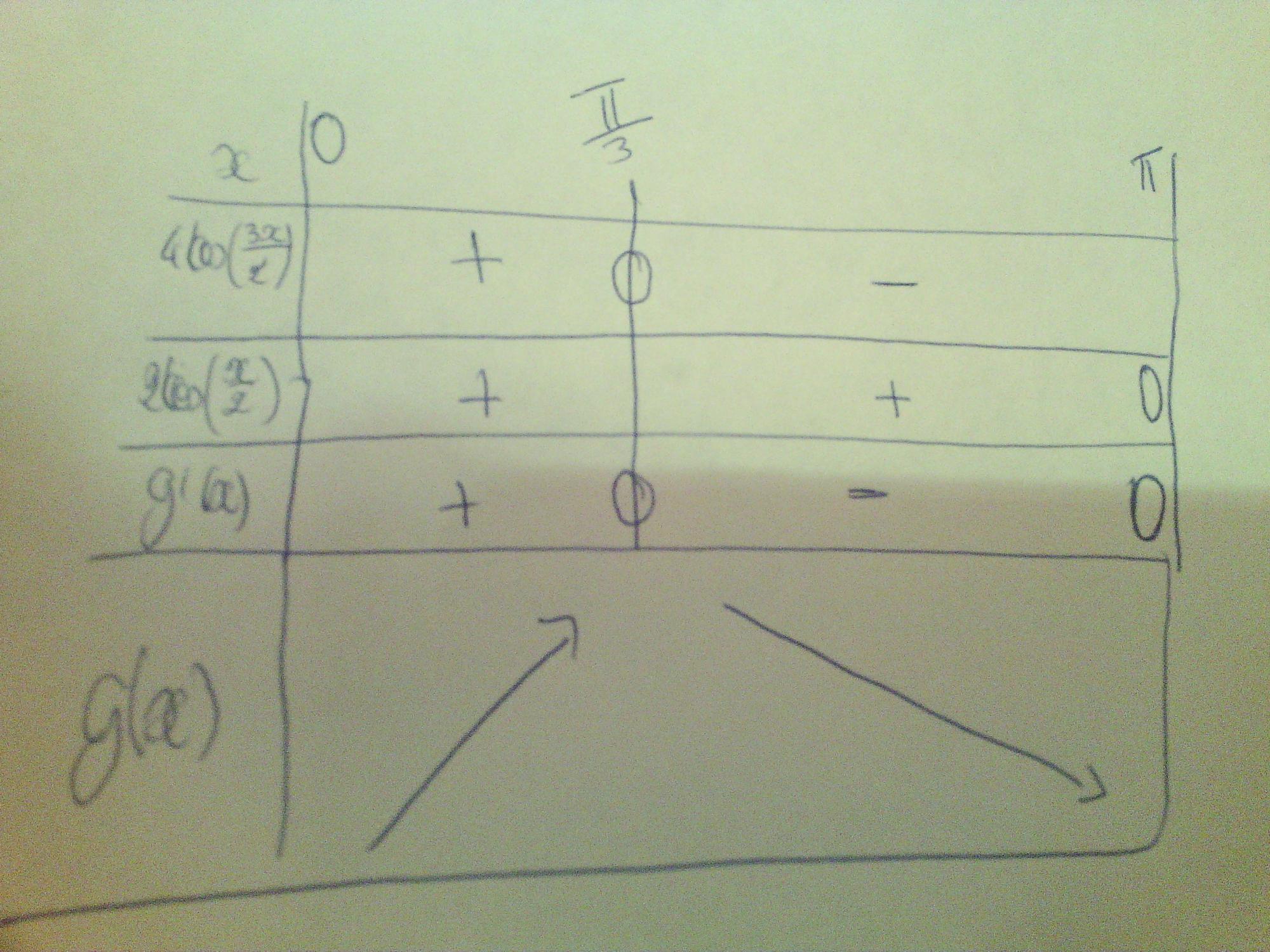
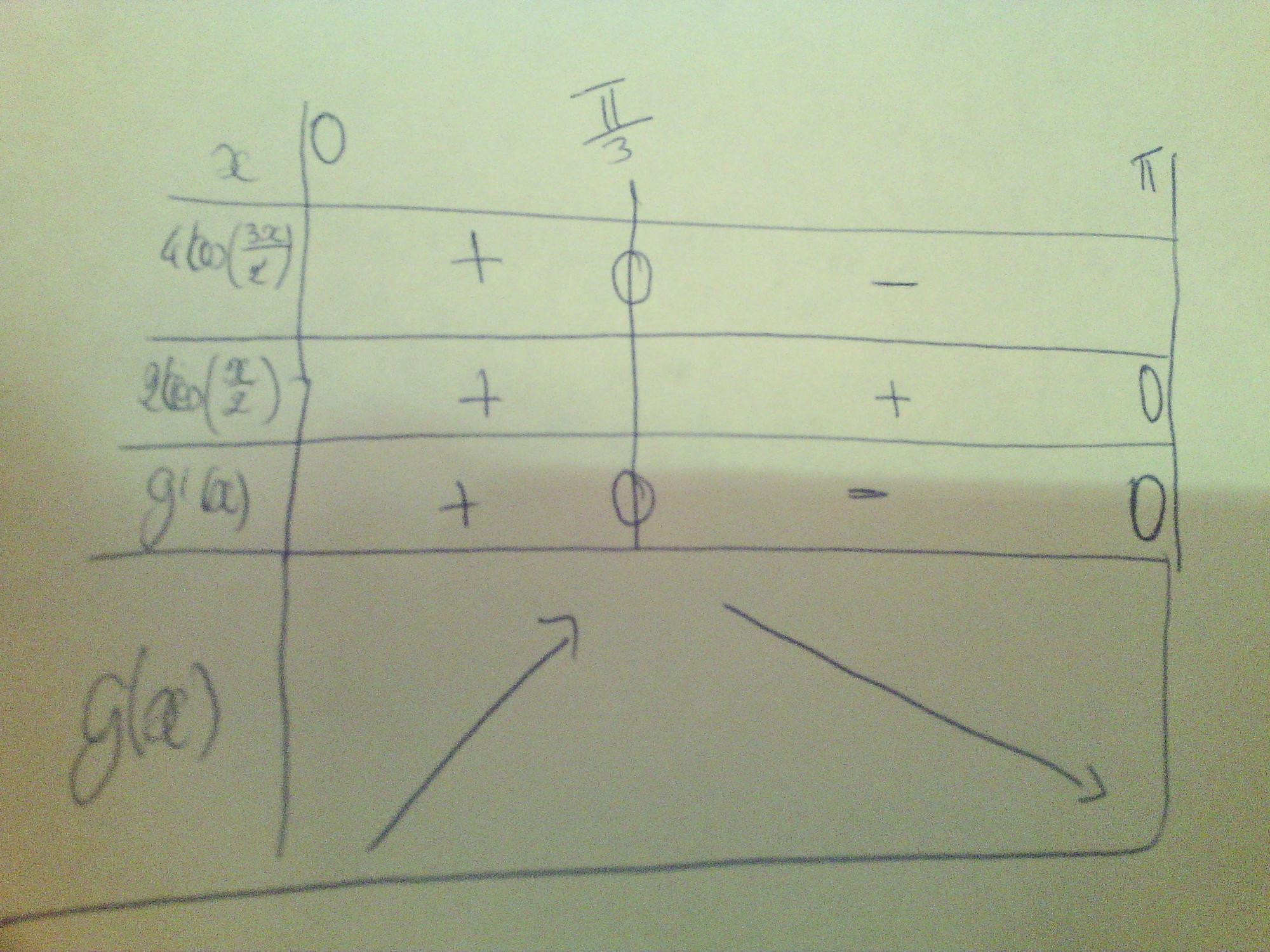
cos(3x/2) est positif sur [ 0 ; pi/3 ] et négatif sur [ pi/3 ; pi ]
ainsi 4 cos(3x/2) est positif sur [ 0 ; pi/3 ] et négatif sur [ pi/3 ; pi ]

et pour le signe de cos(x/2) on a :

cos(x/2) pour x € [ 0 ; pi ] ,ainsi pour x/2 E [ 0 ; pi /2 ]
0<= x/2 <= pi/2
<=> 0 <= x <= pi
donc cos(x/2) est positif sur [0; pi]

ai-je toujours bon ?

[PlaneteF]

Enchaîne, enchaîne ...

[invite6488a89f]

Enchaîne, enchaîne ...

4 cos(3x/2) est positif sur [ 0 ; pi/3 ] et négatif sur [ pi/3 ; pi ]
2cos(x/2) est positif sur [0; pi]
et sa s'annule en pi je croi
donc en dresse le tableau de signe de g'(x) :

[PlaneteF]

et sa s'annule en pi je croi

Les maths ce n'est pas une question de croyance ... et ça ne s'annule pas qu'en

[invite6488a89f]

Les maths ce n'est pas une question de croyance ... et ça ne s'annule pas qu'en

en pi / 2 ou 0
comment savoir si s'annule pour cos (x/2) vu qu'il est positif sur [ 0 ; pi ]

[PlaneteF]

en pi / 2 ou 0

Franchement, comment veux-tu y arriver, ... tu balances des tonnes de résultats au pif, sans vérifier quoi que ce soit. Si tu veux que l'on t'aide, commence par t'aider toi même

Tu peux quand même voir par toi même que :






Et donc ne s'annule ni en , ni en

[invite6488a89f]

Franchement, comment veux-tu y arriver, ... tu balances des tonnes de résultats au pif, sans vérifier quoi que ce soit. Si tu veux que l'on t'aide, commence par t'aider toi même

Tu peux quand même voir par toi même que :






Et donc ne s'annule ni en , ni en

bas j'ai trouvé que g'(x) ne s'annule ni en pi/3 ni pi/4 ni en pi/6
donc je sais pas comment faire ...
Ce devoir me fatigue quand même un peu beaucoup .. je n'en vois même plus la fin ...

[PlaneteF]

bas j'ai trouvé que g'(x) ne s'annule ni en pi/3 (...)

[invite6488a89f]

pourquoi 4 cos(pi/2) ?

[PlaneteF]

Pour ,

(soupirs)

[invite6488a89f]

Pour ,

(soupirs)

oui oui c'est je me suis tromper en refaisons le calcule j'ai mis pi/6 au lieu de pi/3 c'est pour sa que je comprenais pas désoler ... en plus de ca si vous avez vu la photo que j'ai mis sur le signe de g'(x) j, j'avais bien mis que g'(x) s'annule en pi/3 et en pi