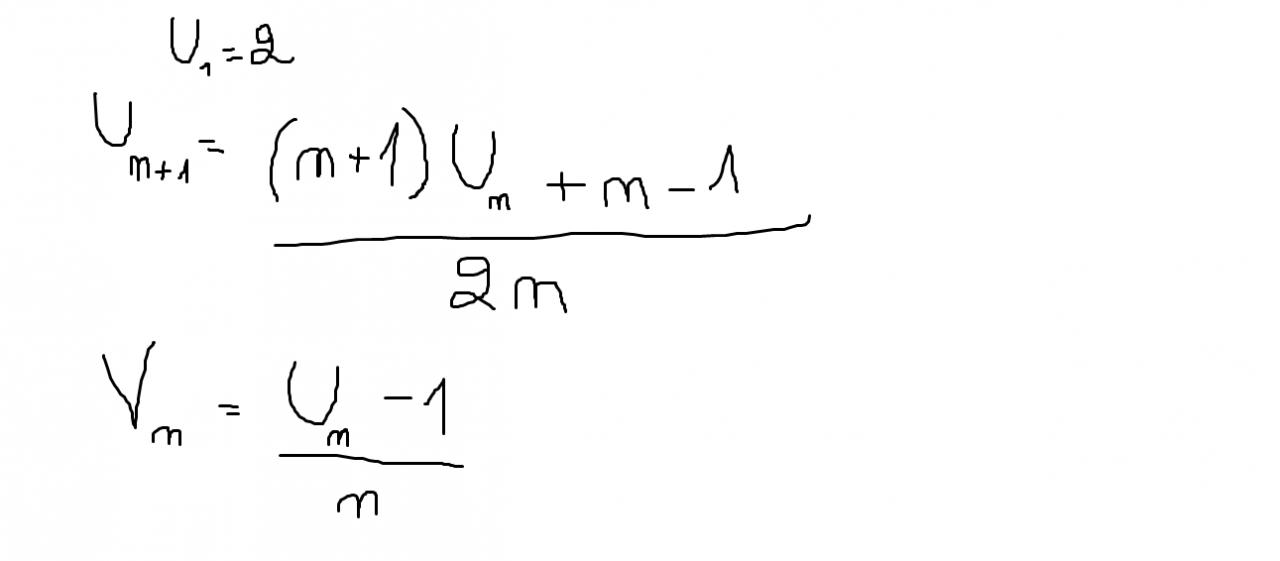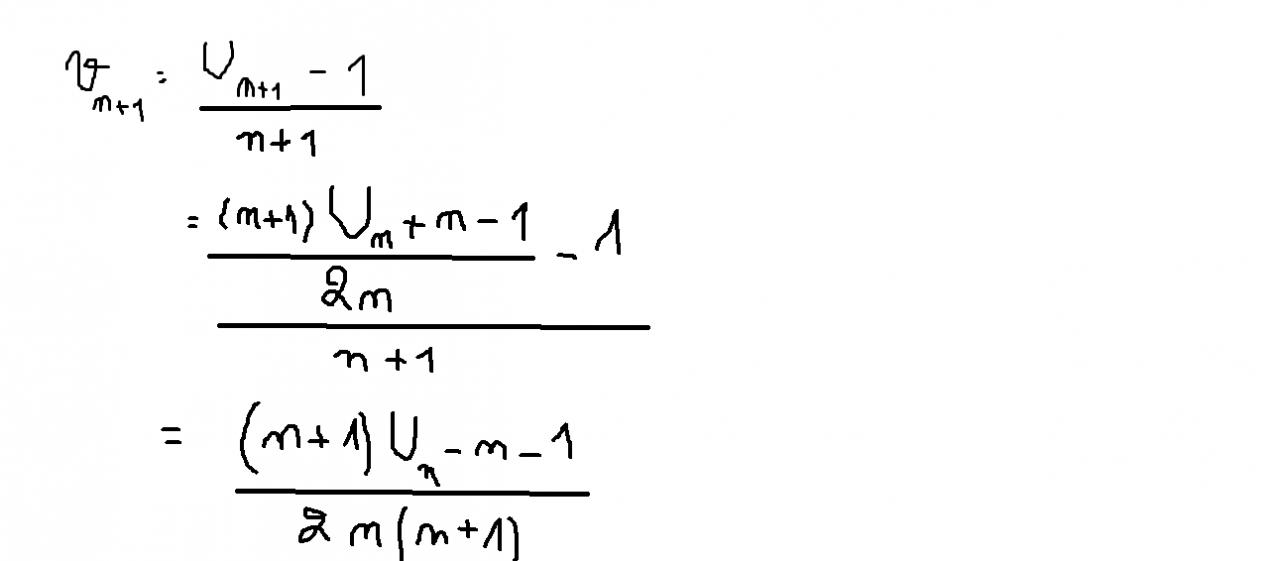bonjour/bonsoir, est ce que quelqu'un peut m'aider dans cette question?: "on considère la suite (Un) définie pour tout entier naturel n non nul par son premier terme U1=2 et la relation de récurrence U(n+1)=(n+1)Un+n-1/2n .on considère la suite Vn=Un-1/n
il faut montrer que (Vn) est géometrique.
ce que jai essayé:
par definition V(n) est geometrique si V(n+1)=q Vn
Vn= Un-1/n
V(n+1)= U(n+1)-1/n+1
=(n+1)Un+n-1-1/2n/n+1 (on simplifie n+1)
=Un+n-2/2n
ensuite...?
merci pour votre aide.
Bonjour.
Tu as écrit :
Vue la suite du texte (la simplification), je crains que ce ne soit pas ça. peux-tu donner l'énoncé corrigé (avec les parenthèses nécessaires à cause des règles de priorité des opérations, par exemple 2/5+3 fait 3,4, alors que 2/(5+3) fait 1/4=0,25) ou confirmer que j'ai écrit le bon énoncé.
Cordialement
salut, merci de m'avoir répondu, voici l’énoncé mieux ecrit
salut,Envoyé par thekimo
dans ce que tu as fait au dessus il y a un leger problème : tu ne peux pas passer de la ligne 2 à la ligne 3 en simplifiant par n+1 ... les additions t'en empêches... à moins que le n+1 ne divise que le (n+1)*Un mais vu comme tu l'as écrit je ne pense pas
bonne journée
merci pour la pièce jointe, en effet c'est plus clair
du coup, repartons de v(n+1)
on a :
ensuite tu remplaces Un+1 comme tu l'as fait ainsi que n
on arrive sur
voila je te laisse finir le raisonnement .... il te reste quatre étape : un développement, deux factorisation et un simplification et tu trouves que ta suite est géométrique
bonne soirée
EDIT : j'ai un problème avec LaTex du coup je ne vois pas les formules donc je ne vois pas si mon code est bon ou s'il y a des fautes XD ... si quelqu'un pouvais me le dire
bonsoir,
j'ai essaye de le refaire:
mais je ne vois pas comment le developement va t-il m'aider ?
-n-1=-(n+1) (formule de cinquième sur le - avant une somme, utilisée à l'envers)
Cordialement.
merci jai reussi à le faire.
c'est bien si tu as trouvémais je ne vois pas comment le developement va t-il m'aider ?
bonne journée
