Suites arithmético-géométrique et homographique

[invite415ba938]

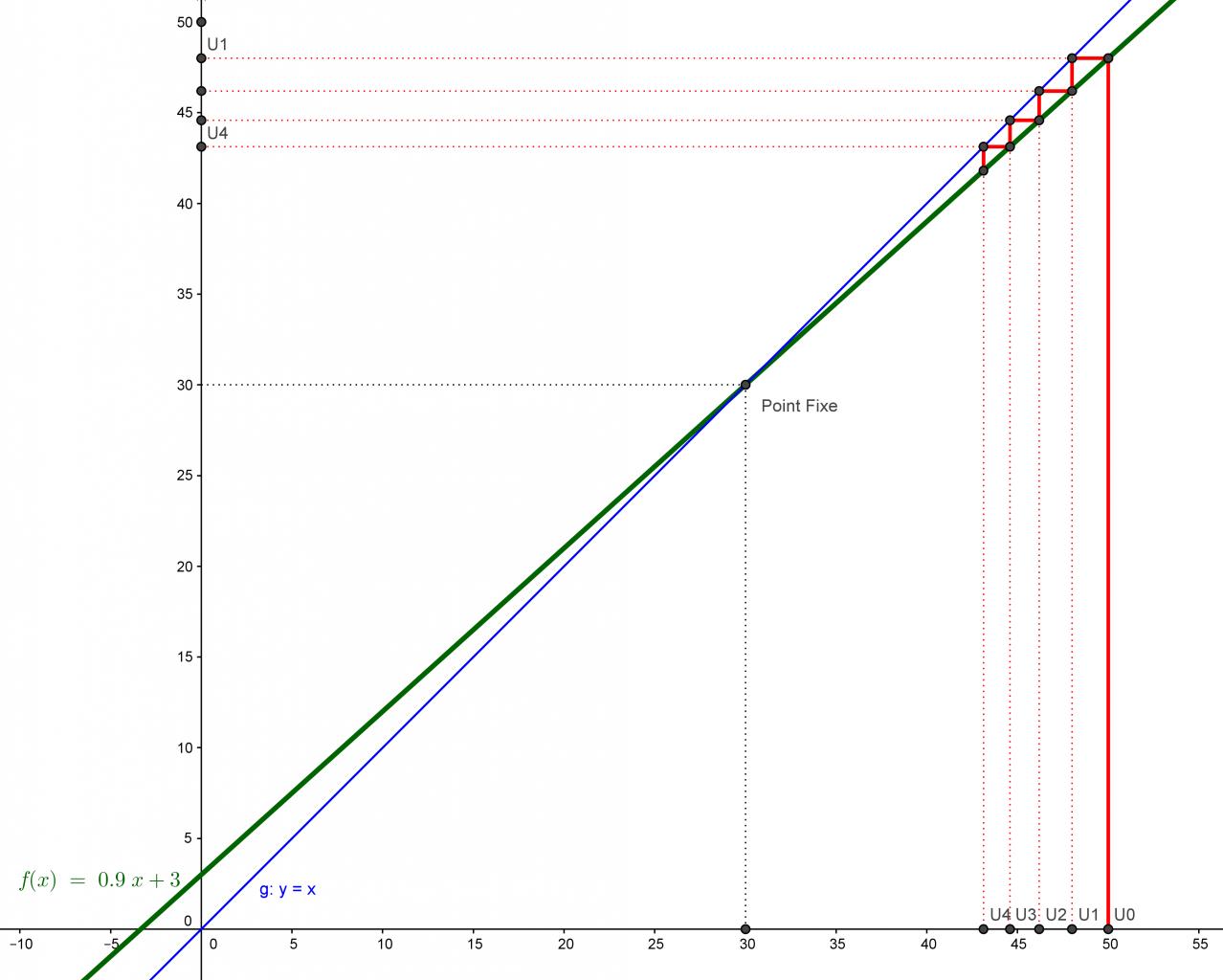
Bonjour, je suis en TS et j'ai un DM à rendre dans lequel on me demande de trouver :
- la suite explicite d'une suite arithmético-géométrique à partir de la forme de récurrence
- la suite explicite d'une suite homogaphrique à partir de la forme de récurrence.


Suite arithmético-géométrique :
U0 = 50
Un = 0.95Un + 3

J'ai du mal à trouver la suite auxiliaire Vn, j'ai regarder sur plusieurs forums mais je n'ai pas compris grand chose....

Pour la suite homographique,il me manque la façon de trouver la suite auxiliaire Vn d'une forme arithmético-géométrique que j'appliquerai ensuite au dénominateur et au numérateur.

Merci de me répondre
-----

[zenxbear]

déjà, c'est une relation de recurrence.

2/ Tu as essayé de dessiner cette suite? Tu visualises ce qui ce passe?

si tu faisais un dessin:



tu verrais un point fixe solution de (?). dont l’abscisse est une valeur particulière tel que si
U0'=cette valeur, alors la suite définie U_n' = 0.95U_{n-1}' + 3 ( qui est la même relation de récurrence que tu as) est en réalité constante!

ta suite "magique" V_n est en fait "U_n- cette valeur".

Si tu initialise ta suite avec une valeur U0=10 par exemple. ta suite va augmenter... vers cette valeur magique.

[invite415ba938]

Merci beaucoup, j'ai compris
Juste une question, quel application utilisez-vous pour avoir un graphique comme ça?

[ansset]

globalement pour une Suite arithmético-géométrique :
U(n+1)=aUn+b avec a diff de 1 ( sinon la suite est arithmétique )
on pose Vn=Un-b/(1-a)
et on retrouve
V(n+1)=aVn

[A voir en vidéo sur Futura]

[zenxbear]

n'oublie plus jamais d'ou sort ce b/(1-a).

sinon le dessin tu fais ça sous géogebra. Mais tu dois pouvoir le faire à la main. A partir du moment ou tu sais tracer sur un papier 2 droites y=x et y=0.9x3, il ne te reste plus qu'à faire schématiquement l'escalier, et visualiser si la suite se rapproche du point fixe, ou s'en éloigne!

Yvan Monka sur math et tiques a un fichier géogebra => cf Représentation des termes d'une suite arithmético-géométrique
le truc, est que ca ne couvre pas ton mini exo, puisque u0=50...
mais l'idée est la même.

Moi je préfère dessiner cela différemment. cf Regarde son fichier Limite d'une suite définie par récurrence. Ca demande de faire appel au tableur sous géogebra, pour positionner les points sur le graphique. Reste plus qu'a les relier.
tu peux dans ce template remplacer la definition f(x) par la valeur que tu as f(x)=0.9x+3... mais u0=50 est toujours hors limite.

[ansset]

Pour la suite homographique,il me manque la façon de trouver la suite auxiliaire Vn d'une forme arithmético-géométrique que j'appliquerai ensuite au dénominateur et au numérateur.

là, je ne comprend pas ce que tu veux faire !?
ce n'est pas ainsi qu'on traite une fonction homographique.
soit par exemple:
U(n+1)=(aUn+b)/(cUn+d) donc une fonction type
f(x)=(ax+b)/(cx+d)
tu peux la ramener à une forme du type
f(x)=a'/(x-b') + c'
avec un nouveau repère centré en (b',c') on trouve
f(X)=a'/X

[invite415ba938]

Merci pour toutes vos réponses!