probabilités dans les échecs

[invited8d9e610]

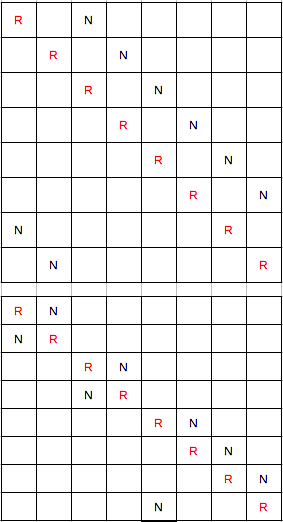
bonjour tous le monde
j'ai un exercice sur le nombres de possibilités de placer des tours sur un échiquier (je pense que ce genre d'exercices
est connu)
mais j'ai un exercice qui est un peu modifié et moi qui aie déjà un problèmes avec ce genre d'exercice je vous demande de l'aide
alors pour mieux comprendre je vais plutôt poser une question classique puis je passerais a mon exercice
combien y a t il de possibilités pour placer 8 tours dans un échiquier 8*8 de façon a ce que dans chaque lignes et chaque colonnes il n'y a pas plus d'une tour
pour ce genre de question je ne sais pas si je dois compter avec les cases ou avec les colonnes (ou les lignes)
parce que je vois deux cas de figures
1/ je prend la première tour et elle a le choix de se placer dans 64 case
puis la deuxième a le choix dans 49 puis la 3ème dans 36 ainsi de suite
ainsi les possibilités sont 64*49*36*25*16*9*4*1 or (8!)²
2/ je pars du faites que chaque tour est dans une ligne( ou colonne) pus la première tour peut se placer dans 8 colonne (ou ligne) puis la deuxième
dans 7 puis la 3ème dans 6 ainsi de suite ce qui donne un nombre de possibilité égale a 8!

merci de m’éclairer a ce sujet je ne sais qu'elle méthode est la juste
ce qui m'aiderais a résoudre cette exercice dont la question est
quelle est le nombre de possibilités pour placer 4 tours blanches et 4 tours noirs dans un échiquier de 8*8 de façon a ce que
dans chaque ligne et chaque colonne il n'y ai pas deux tours de la même couleur
si je prend le raisonnement des cases et prend les tours noirs et la première a le choix de 64 cases puis la 2ème 49 puis la 3ème 36 cases
la 4ème 25 cases en suite pour les tours blanches la première peux se placer dans n'importe quelle case
mais en enlevant les 4 cases des tours noirs elle aura donc 60 cases possibles la 2ème blanche dépendra de l’emplacement de la première
si la première ne contiens pas de tour noirs dans sa ligne ou colonne alors la deuxième aura 45 cases possible
si elle contiens une tour noir dans sa lignes ou sa colonnes alors la 2ème aura 46 cases possible
si elle contiens une noir dans ligne et une noir dans sa colonne alors la 2ème aura 47 cases possibles
puis avec en fonctions de chaque cas résultent d'autres cas ce qui prend beaucoup de temps
et donnera un nombre très très grand
et dans cet exercice je ne pense que je puisse utiliser le raisonnement des colonnes
merci de m'aider et de m’éclairer sur ces nombreux points
-----

[gg0]

Bonjour.

Tes résolutions traitent des problèmes différents. Dans le 1, tu as un ordre sur les tours que tu places, pas dans le deuxième (l'ordre n'est donné que par le numéro de ligne.

Donc quel est le problème réel : Placer les tours T1, T2, T3, ... T8 sur l'échiquier ? Ou bien placer 8 tours, en considérant que échanger deux tours donne le même placement ?

Cordialement.

[invited8d9e610]

le probleme c'est le nombre de possibilites a placer ces 8 tours
et je n'ai pas trop compris ton post Gg0

[invite51d17075]

la réponse 2 me semble fausse , puisse que tu dissocies lignes et colonnes.
quand à la première , elle est juste si tu numérotes tes tours , sinon ( si elles sont équivalentes ) il te faut diviser ton résultat par 8!

[A voir en vidéo sur Futura]

[gg0]

Midorima,

si tu ne sais pas ce que tu veux compter, comment compter juste ? Tu ne vois pas la différence que je fais ???? prends le temps de bien lire.

[invited8d9e610]

et bien vu que dans l'enoncé il est question de placer 8 tours
je pense que cela devrais etre 8! non ?

[gg0]

L'énoncé "placer 8 tours" n'est pas suffisant pour décider ce qu'on veut dénombrer. Si c'est placer 8 tours numérotées de 1 à 8, c'est ton 1 qui convient, si c'est des tours dont on ne s'occupe pas de distinguer laquelle est à telle ou telle place, si échanger deux tours ne change rien, on trouve effectivement 8! On peut justifier ton calcul, mais il faut une explication plus claire. Par exemple dire "pour la tour qui est dans la ligne 1, on a 8 positions possibles. Une fois cette position choisie, il n'en reste que 7 pour la tour de la ligne 2, " etc.

Cordialement.

[invited8d9e610]

Merci pour ta reponse
maintenant j'aimerais passer a l'exercice avec les couleurs
l'enonce n'a pas dis 4 tours numerotées ou un truc du genre il a juste dis 4 tours blanches et 4 tours noirs
donc si je prend les 4 tours noirs je peux trouvé le nombre de possibilités 8*7*6*5 mais comment ajouter les tours blanches est ce que ce serais
(8*9*6*5)² mais dans ce cas coment faire puisque si il y a dans une ligne une blanche et noir elle peuvent etre dans le meme emplacement
voila pourquoi je pense qu'il faut utiliser le nombre de case

[invite51d17075]

RE-
pour ma part, je comprend mieux ta démo par la piste 1.
( pas compris ton calcul avec la démarche 2 )
d'où pour le premier cas (8!)²/8!=8! si les tours sont non différentiés. ( division ad hoc )
ici je ferais de même, sachant que, pour une répartition donnée le nb de combinaisons équivalentes ( le diviseur ) n'est plus 8!

en supposant que tu parles de la couleur des tours et pas de la couleur des cases sur lesquelles se trouvent les tours.

[invited8d9e610]

Bonjour
ansset
oui je parle de la couleur des tours non des cases
et dois je comprendre que pour resoudre l'exercice je dois raisonner avec les cases ?

[invite51d17075]

disons que je trouve la résolution plus simple avec cette démarche ( soit la 1)) pour toi.(*)
On compte toutes les répartitions possibles, en les plaçant à la suite.
On divise par le nb d'arrangement équivalent ( tours similaires ) soit donc dans ton premier cas
(8!)² diviser par 8! , d'où résultat de 8!
dans ce deuxième cas , le (8!)² reste le même , il n'y a que le diviseur qui change. ( à toi de réfléchir : combien de permutations possibles pour les blanches, ainsi que pour les noires ? )

(*) tu arrives au même résultat dans ton approche 2) mais je ne comprend pas ta démo ( et si elle est juste ), donc je ne vois pas comment l'étendre pour ce nouvel énoncé.

[invited8d9e610]

pourquoi ça resterai (8!)² ??
ici on peut mettre 2 tours de différentes couleurs dans une même ligne ou colonne
en raisonnant avec les cases on a 64*49*36*25 pour les 4 tours noirs
et pour les tours blanches c'est une tout autre histoire
pour placer une blanche elle a 60 cases possibles et les 3 autres dépendra de la première placée
si elle contiens des tours noir dans sa ligne ou colonne ou non
je ne vois pas pourquoi cela restera (8!)²
et j'ai une autre question
pourquoi faut il diviser par quelque chose quand les tours sont les mêmes ?

[invite51d17075]

pourquoi ça resterai (8!)² ??
ici on peut mettre 2 tours de différentes couleurs dans une même ligne ou colonne

ben, il aurait fallu le préciser quand même !!!
pas le temps de voir ton calcul

pour la dernière question , tu vois bien par exemple que si tu ne places que les tours noires tu as 4! façons de les placer aux mêmes endroits car tu les places au fur et à mesure et l'ensemble des positions
{p1;p2;p3;p4}, {p2;p1;p3;p4}, {p4;p3;p1;p2}, etc ..... est la même au final

[invited8d9e610]

bonjour
ansset
tu voudrais bien detaille plus ta demonstration
parce que je ne comprend pas trop ce que tu fais avec p1 p2 p3 p4
et comment tu sais qu'il y a 4 facon de les placer au meme endroit
et que signifie au meme endroit ? est ce que tu veux dire dans la meme case ?

[invite51d17075]

supposons que te ne places que deux tours.
tu diras que tu as 64*49 possibilités ( la première puis la deuxième )
mais que les places en p1 puis p2 est la même chose que p2 puis p1 , il faut donc diviser par 2.
si tu as 3 tours il faut diviser par 3! possibilités, etc.

concernant ton deuxième énoncé ou les blanches "seraient" indépendantes des noires, je suis un peu surpris, car cela ne simplifie pas du tout le calcul.
peux tu confirmer que c'est bien l'énoncé ?
Cdt

[invited8d9e610]

Bonjour
ansset
l'énoncé est :
quel est le nombre de possibilités de placer dans un échiquier de 8*8 4 tours blanches et 4 tours noirs
de facon a ce que dans chaque ligne ou colonne il n'y ai pas deux tours de la meme couleur

moi ce que je comprend de cetenonce est que dans une ligne ou colonne ou peut trouver soit une ;
- une tour blanche
-une tour noir
-une tour noir et une tour blanche

donc une blanche peut se placer dans la ligne ou colonne d'une noir sauf dans la case ou est la noir

corrige moi s j'ai mal compris l'énoncé

[invite51d17075]

OK, tu confirmes bien ton énoncé.
c'est plus complexe que si elles devaient juste respecter la première règle.
j'ai une idée de démarche mais pas le temps à l'instant.
Cdt

[invited8d9e610]

Moi j'ai deja exposé mon idée mais je ne sais comment continuer
quand tu aura du temps ce serai bien déexposer la tienne
Merci de ne pas oublier.

[invite51d17075]

promis !
à toute à l'heure.
Cdt

ps: tu peux tj exposer la tienne, je n'ai pas trop de temps avant la fin d'AM.

[Merlin95]

Bonjour,

personnellement sans donner le détail, je trouve (16 x 7) 112 solutions.
Je suis parti du principe qu'une solution est impossible dès qu'une tour n'est pas mitoyenne (sur la ligne et la colonne) à 2 autres tours, ce qui est assez évident lorsqu'on essaie des solutions, mais qui est plus difficile à démontrer rigoureusement.

[Merlin95]

Il me manque certains combinaisons basées sur le même principe, avec je trouve 210 ((16 + 14) x 7) solutions.

[invite51d17075]

moi ce que je comprend de cetenonce est que dans une ligne ou colonne ou peut trouver soit une ;
- une tour blanche
-une tour noir
-une tour noir et une tour blanche

ben, soit aucune, vu la possibilité d'en avoir deux ( de couleurs diff ).
je trouve la "combinatoire" bien complexe à cette heure ci.

[Merlin95]

moi ce que je comprend de cetenonce est que dans une ligne ou colonne ou peut trouver soit une ;
- une tour blanche
-une tour noir
-une tour noir et une tour blanche

Je ne suis pas parti sur ce type de raisonnement combinatoire.

J'ai essayé de placer les 8 tours de manières à ce qu'aucune ne soit sur la même ligne ou colonne qu'une autre. Et finalement le nombre de case de l'échiquier n'étant que 8x8, on se rend compte qu'on a pas beaucoup le choix.

La solution générale et la plus simple étant de les placer ainsi :
tour.png

Ensuite j'ai compté les variantes (finalement j'en trouve 2240) correspondant à ces variations :

(on fait varier les couleurs sur la diagonales)
tour2.png

(on décale un carré RNRN (ici le troisième sur la diagonale) diagonalement)
tour3.png

Et finalement on décale la "diagonale" vers la droite et vers le bas :
tour4.png
tour5.png

Enfin on peut faire la même chose en inversant le sens de la diagonale.

Mais c'est plus intuitif, je n'ai pas montré que les seules solutions étaient les solutions de cette forme (chaque tour possède deux tours adjacentes).
Il y a donc peut-être (à voir si vous avez une idée) une solution qui n'est pas comprises dans mes solutions.

[invite51d17075]

il y a beaucoup d'autres solutions, rien n'empêche que les tours blanches ne soient pas ( 1 jusqu'à 4) alignées sur une noire.
le cas : "aucune d'entre elles" est le plus simple à résoudre : (8!)²/(4!)²

[invite51d17075]

à multiplier par deux !
je crois de moins en moins à cet énoncé dont la résolution me semble plutôt assez complexe.
mais il se peut que quelque chose m'échappe.
si est tel quel ( sans que le prof s'en soit rendu compte ) ce serait un bon exercice en science ludique.
en attendant quelques matheux du site.....
Cdt

[invite51d17075]

en plus même sur ce cas simple. ( aucune alignée blanche ou noire ) je fais une boulette.
le diviseur de 8!² est C(8,4) ! désolé.

[Merlin95]

Je ne vois pas bien ce que tu veux dire, par "rien n'empêche que les tours blanches ne soient pas ( 1 jusqu'à 4) alignées sur une noire".
Mais j'ai trouvé aussi ce genre ce chose :



En effet, pas trop d'idées, trouver une méthode énumérant tous les cas me semble être un problème complexe.

[invite51d17075]

je ne sais pas faire de tableau comme toi.
ce serait plus simple pour illustrer ce que je veux dire.
mais repense à la première question ou il y a 8 noires sans aucune ligne ou colonne commune, imagine que la moitié d'entre elles soient blanches.
cela représente déjà beaucoup de cas.
ensuite il peut il y en avoir une alignée sur une noire, ou deux, ou une dans un croisement ligne/colonne de deux noires, etc .....

ps :a ce propos, lire A(8,4) et non C(8,4) dans mon précédent mess, décidemment, je suis crevé aujourd'hui, trop peu dormi hier.

[invite51d17075]

ps :a ce propos, lire A(8,4) et non C(8,4) dans mon précédent mess, décidemment, je suis crevé aujourd'hui, trop peu dormi hier.

pétard, grrrrrrr ! nawak
il faut revenir à mon premier calcul (4!)(4!) tous les arrangements possibles des blanches et des noires séparément.
et un facteur 2 en les intervertissant.
shame on me !

[invited8d9e610]

rebonjour
je viens de lire les post et je crois que Merlin95 tu as mal lu ton enoné
(excuse moi si je me trope ) mais il ya 4 tours de chaque couleur non 8
parce que j'ai remarqué que tu mets dans ton échiquier toujours 8 tours blanches et 8 tours noirs
pour ma part je redigerais demain mon début de solution car je suis presque sur que c'est faux vu qu'elle ne se terminera jamais