Propriété peu connue de géométrie entre 2 droites qui coupent un cercle

[1max2]

Je viens de découvrir 2 propriétés des droites coupant un cercle ...Tout le monde sait que l' angle formé sur le cercle , est la moitié de l' angle qui part du centre :voir dessin demo2angles.jpg Il s' agit de démontrer que l' angle O formé par l' arc AB est égal à l' angle C formé par l' arc AB aussi ..la démo est simple, mais attention de bien choisir ses égalités .Je peux la donner si on me la demande ..
Mais quand j' étais plus jeune je soupçonnais l' existence d'un lien entre les angles formés par un point qui n'est pas le centre :
On prend un point E quelconque dans le cercle et on trace 2 droites qui coupent le cercle en BC et AD, et je n' ai pas été surpris de voir que l'angle E était la moyenne des 2 arcs BC at AD (leur angle) demoanglesinterne.jpg
Démo :E est donc le point quelconque de croisement , X est ' langle que forme les 2 segments BD et AC .On considère le triangle CED l'angle ECD =arc(AD/2) Pareil l' angle EDC=Arc BC/2 .Ce sont les 2 arcs qui nous intéressent, on écrit que la somme des angles du triangle ECD=180 et on obtient
ArcAD/2 + ArcBC/2+180-X=180 , et donc X=ArcAD/2 + ArcBC/2 C'est à dire X égal la moitié de la somme des angles qu'il forme : les 2 angles en bleu sur le dessin...

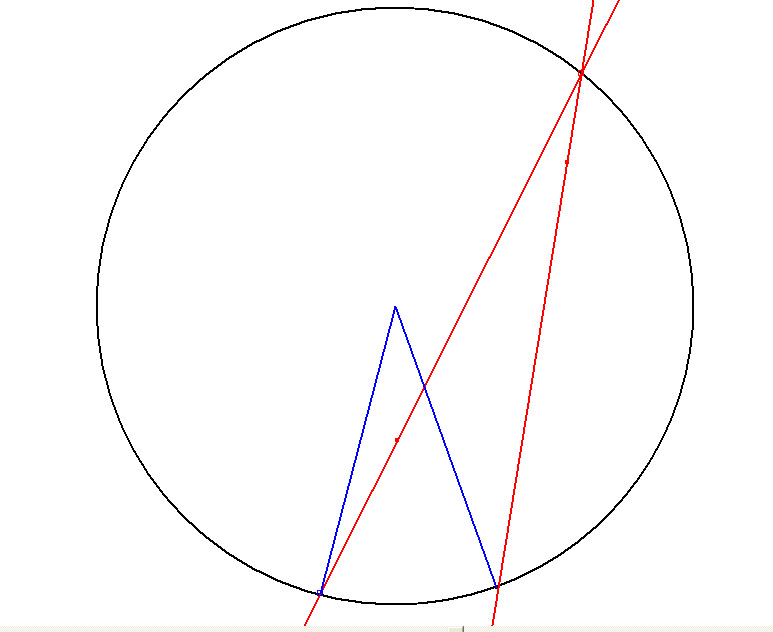
Chose étonnante, quand le point est à l' extérieur du cercle, ce coup ci on fait la différence des arcs formés et non la somme ! C'est l' angle X qui nous intéresse et quel rapport et bingo il a avec les 2 arcs qu'il forme BC et AF (X =(ArcAF-ArcBC)/2
Démo / Elle est simple, mais pour la trouver ne pas partir dans tous les sens !

On considère les triangles FHO et HAG ils ont un angle égal donc la somme des 2 autres angles est égale : L'angle HOF=ArcAF/2 , Pour la commodité j' écrirai ArcAF=AF j'écris que la somme des 2 angles opposés à H est égale (On considère les triangles FHO et HAG) et j'obtiens comme HFO=CD/2 ( arcCD/2)
CD/2+DE=BE/2+ X ..... Or BE=BC+CD+DE ... On obtient CD/2+DE =BC/2+ CD/2+ DE/2 +x et Bingo
X=(DE-BC)/2 =(AF-BC)/2 puisque AF =DE (angles opposés)
On voit donc qu'il y a continuité quand on trace 2 droites qui coupent un cercle, où que se situent ces points, au centre, à l' intérieur ou à l' extérieur !
A mon avis cela devrait servir à démonter la puissance d'un pt par rapport à un cercle...A suivre !


demo-point-exterieur.jpg
-----

[invitedd63ac7a]

Je peux la donner si on me la demande ..Mais quand j' étais plus jeune je soupçonnais l' existence d'un lien entre les angles formés par un point qui n'est pas le centre :

Bravo pour vos recherches si celles-ci vous passionnent. On ne peut que vous encourager à continuer. Ces propriétés des angles inscrits sont connues depuis fort longtemps, au moins depuis 2500 ans. Elles étaient même enseignées au Collège il y a quelques décennies. Le Collège aujourd'hui et le Lycée les ont complètement éliminées des programmes parce que la géométrie n'est plus à la mode aujourd'hui : trop compliquée pour les élèves et inadaptée dans l'optique des programmes postbac.
La géométrie classique reste cependant une activité passionnante, je le répète, n'hésitez pas à explorer ces terrae (in)cognotae.

[1max2]

Merci pour votre réponse et vos encouragements, mais j' ai pratiqué la géométrie à un très bon niveau, mais je n' ai jamais eu affaire à ces propriétés que vous estimez connues depuis 2500 ans, pouvez-vous me donner un lien..Moi, je connaissais très bien la puissance d'un point par rapport à un cercle, et je me fais fort de trouver une démo simple, en rapport avec ce que j' ai démontré, mais j' emploierai alors surement le calcul vectoriel
Vous me parlez de propriétés d' angles inscrits ..dans un cercle je suppose .Moi dans tous les pb que j' ai eu à faire , je n' ai jamais rencontré cette éventualité, même si sans doute cela tournait autour .Comment être certain que vous ayez bien compris le sens de mon post ?
Résumé : cela m'étonne beaucoup que cette propriété que je n' ai jamais rencontré durant mes études et les pb de géométrie soit connue depuis 2500 ans , mais je peux me tromper évidemment !

[invitedd63ac7a]

Les mathématiques, et pour ce qui vous concerne, la géométrie exhibent une multitudes de propriétés que l'on peut montrer et qui sont souvent à l'origine d'exercices d'école. Toutes ces propriétés qui n'ont pas le statut de théorème, car considérées par la communauté mathématique comme des résultats mineurs sans grandes conséquences, existent et peuvent être démontrées. D'ailleurs, une certaine familiarité avec la géométrie et ses figures, comme cela semble le cas pour vous, fait découvrir facilement des propriétés, parfois étonnantes (c'est d'ailleurs une grande qualité de cette vielle Géométrie, ô combien délicieuse), qui ne sont pas répertoriées dans les livres mais qui n'en sont pas moins réels et en général démontrables de façon élémentaire.
Apparemment c'est ce que vous avez fait.

Comme je vous l'ai dit votre travail d'amateur est louable. Maintenant qu'attendez-vous de ce forum en présentant vos résultats par le menu ?

Je n'ai pas de lien à vous donner, vous trouverez des pistes dans les anciens manuel de mathématiques des Lycée d'avant 1960-70, c'est à dire avant la réforme des math modernes. A l'époque où l'on faisait encore de la Géométrie au Lycée. On peut trouver de tels ouvrages numérisés sur Galica-BNF, dans les Anciens fonds des Bibliothèques municipales.

Attendre l'avis d'autre personnes...

[A voir en vidéo sur Futura]

[1max2]

Sur facebook, un ami demande si quelqu'un sait résoudre un pb de géométrie, alors je me prends au jeu et je planche ..Avec les logiciels de géométrie maintenant c'est bien plus simple, et je vois que quand 2 droites sécantes croisent un cercle on a ce résultat, et qu'il fallait s'en servir pour résoudre le pb .Je n' ai plus de nv de l 'ami en question, il s'est complètement volatilisé
J' ai eu envie de mettre ce résultat quelque part, car on a vite oublié la façon de procéder ..
Je m' étonne tout de même que ces résultats soient connus depuis 2500 ans sur quoi vous basez-vous pour affirmer cela?
.La puissance d'un point par rapport à un cercle a été introduite par Jakob Steiner en 1830 d' après ce que j' ai trouvé sur internet .
.Je m' étonne que ce que j' ai trouvé ne soit pas enseigné car je suis certain que ce la aiderait à résoudre plus facilement beaucoup de problèmes..
J'ai étudié la géométrie à un bon niveau pendant les vacances 1967 dans la classe de mon père pour passer le concours d' entrée à l' Ecole Normale d'instit .Une dictée/questions et un pb de math par après midi sur les anales du concours dont je suis sorti premier, et très déçu effectivement qu'en seconde on ne continue ni les dictées, ni la géométrie .Mon prof de math m ' affirmait qu' avec la géométrie vectorielle on résolvait tout ! Je n' en ai jamais été convaincu , par exemple pour démontrer que les 3 angles d'un triangles est plat rien ne vaut la démo géométrique qui est belle et simple ! ..
J'invite les profs de géométrie du collège à enseigner ces résultats ainsi que la démo à leurs élèves ! Quand 2 droites sécantes coupent un cercle , elles partagent ce cercle en 2 arcs l' angle que forme ces droites est la somme géométrique des 2 arcs créés (Arc1+ arc2)/2 ou la différence quand les droites se coupent en dehors du cercle . Cas particulier quand le point de croisement est sur le cercle on retrouve angle = arc créé /2 C'est une propriété plus générale que celle ci .
Cas particulier l'angle rouge est la moitié de l' angle bleu !

[gg0]

Bonjour.

Appeler "bon niveau" ce qu'on faisait en troisième pour le concours d'instituteurs (*) est manquer de jugeote : Il y avait encore de la géométrie en seconde, première et terminale math-élem. Puis des certificats de géométrie en fac de science pour la licence, et encore des formations de géométrie après...
Ce qu'on faisait en collège et lycée à cet époque étai qualifié de "géométrie élémentaire". Il est vrai qu'on ne rencontrait pas le résultat que tu cites dans les études de géométrie élémentaire de troisièm, mais pas non plus des tas de propriétés géométriques qui on été enseignées à cette époque au lycée, puis ne sont plus enseignées au profit d'autres.
D'autre part, seule ton ignorance peut justifier ton " Je n' en ai jamais été convaincu", puisque tu ne peut affirmer cela que faute d'en avoir vraiment fait. à un niveau universitaire.
Enfin, comme tous les amateurs qui ne se renseignent pas, tu considères que ce que tu as trouvé seul est "très important", c'est classique : Tu n'as aucun recul possible, tu ne connais pas l'ensemble des domaines de développement de la géométrie. Mais évite de te ridiculiser plus : ton adresse aux profs de collège m'a bien fait rire. Tu ne sais sans doute rien des programmes actuels de collège (faits pour 90% d'une classe d'âge, pas 15% comme à notre époque), mais on n'y fait que très peu de géométrie. Et le travail des profs est de faire le programme, pas de satisfaire à des envies individuelles.

Cordialement.

Et quand même bravo pour cette propriété !

(*) Je connais, je l'ai passé. Et comme je l'ai raté, d'ai dû devenir prof de maths

[1max2]

Merci pour les encouragements .Connaissiez-vous cette propriété ?
Manquer de jugeote ...Mmmmm .Vous me dites que vous avez raté le concours, et que vous avez fait prof de math ! J' ai une voisine prof de math,et pour passer son concours elle est venue me voir ..
Je crois être le seul à avoir fait complètement le pb de géométrie pour ce concours d'Instit..Les pbs que je faisais pour m'entrainer que mon père trouvait sur les anales je ne les avais jamais vus en en collège.Il y avait une partie orale à ce concours, je me souviens j' ai eu à démontrer la puissance du point % à un cercle, je l' avais déjà traité c'était du gâteau .Suis sorti 1 er du concours ! Ensuite en 1969 à une année près plus de géométrie en seconde C ni première, je me souviens j' avais été très déçu, c'était tout vectoriel, j' avais demandé au prof étonné"Mais on résout tout avec les vecteurs ? " Il me dit oui .Il n' empêche, je suis allé voir sur wikipédia, un gars proposait une démo vectorielle de la puissance d'un point, alors qu'en prenant 2 triangles semblables, on a le résultat de suite :j ' ai fait une petite modif en ajoutant ma démo qui tient 3 lignes !

!Je propose une autre démo qui me semble plus simple et géométrique, et qui peut être abordée en 3 ème sans passer par le produit scalaire . On trace BC et DA et on considère les triangles MAD et MCB :ils sont homothétiques : 2 angles égaux donc on a de suite MD/MB=MA/MC et MA X MC=MB X MA CQFD ce qui montre que le produit est indépendant de sa position . pour le cas tangent on considère les triangles TBM et TAM pareil ils ont 2 angles égaux sont homothétiques et MB/MT=MT/MA>>> MT²=MA x MB.... 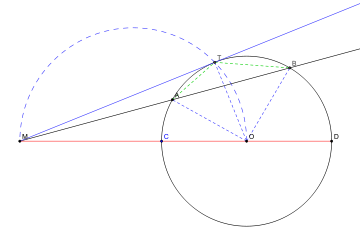https://commons.wikimedia.org/wiki/F...svg?uselang=fr Je joins le dessin de wikipédia, pour avoir accés à la démo il faut cliquer sur l' onglet Démonstration !

[1max2]

Pour gGo , je ne vous ai pas dit qu' à 40 ans vers 1994 donc j' ai passé un deug de math physique par correspondance,(j' ai transpiré pour me remettre ne serait qu'au niveau bac et pouvoir suivre), car les calculatrices étaient passés par là et les courbes étudiées moins pépères! ) juste pour ma culture personnelle, c'est la physique qui me passionne, et j' ai pu notamment après cette "remise à niveau" travailler sur l' expérience de Michelson et Morley, et découvrir des tas de choses sur la relativité restreinte, ce qu'en pensait Poincaré et la gravité avec notamment une démonstration géométrique simple du théorème" La gravité est nulle à l'intérieur d'une coquille sphérique homogène" . ..Si cela vous intéresse je l' ai sur mon site personnel !

[gg0]

Il n'en reste pas moins que c'est de la géométrie élémentaire.

[1max2]

Bien entendu c'est de la géométrie élémentaire,qui semble vous échapper, mais je répète ma question, "Connaissiez-vous cette géométrie élémentaire et notamment cette propriété que j' ai démontrée? ".
De plus vous semblez, peut être afin de vous grandir me sous -estimer, or comme je vous l' ai signalé j' ai poursuivi mes études en passant un deug de Math/ physique par correspondance à 40 ans avec succès, et j'ai eu aussi plusieurs discussions sue ce forum sur le sujet pointu de l' effet Sagnac connaissez vous le sujet ?
Je vous pose 2 questions simples , merci d'y répondre .
1/ Connaissiez-vous cette géométrie élémentaire dont je parle et cette propriété générale des droites sécantes sur un cercle, quelque soit le point de départ des droites?
2/Connaissez-vous l'effet Sagnac?
Quant à moi, sur l'effet Sagnac j' ai démontré que l'on pouvait admettre certes que la vitesse de la lumière était constante, mais sur un aller/retour et qu'elle pouvait être différente sur l' aller et sur le retour comme je l' ai montré dans l' expérience Michelson /Morley ! ..Merci donc de vous excuser, non, je ne manque pas trop de jugeote, même si je peux me tromper .
Voici la discussion sur l'effet Sagnac sur ce forum, modèle selon moi de discussion, tout le monde a su apporter sa compétence, et vous remarquerez que personne n' a répondu à ma dernière intervention, dans laquelle je suppose que la vitesse de la lumière est différente dans l' aller et dans le retour : merci de répondre à mes questions !le lien https://forums.futura-sciences.com/p...-einstein.html

[gg0]

Non, je ne connaissais pas cette propriété, comme je ne connais pas les milliers de propriétés du même genre du fond des exercices de géométrie élémentaire qui se faisaient il y a plus de 50 ans.

Quant à l'effet Sagnac (c'est ton nom ?), je ne connais pas non plus, mais ce que tu en dis à la fin ne m'incitera pas à aller lire. Il y a déjà trop de prétendus inventeur en maths sur les forums pour que j'aille regarder de la physique.
En général, quand personne ne répond dans un forum, c'est qu'il est inutile de continuer, pas que le dernier qui a parlé a raison.
Mais comme tu aimes bien être le dernier à parler, je te laisse à tes prétentions.

[obi76]

Voici la discussion sur l'effet Sagnac sur ce forum, modèle selon moi de discussion, tout le monde a su apporter sa compétence, et vous remarquerez que personne n' a répondu à ma dernière intervention, dans laquelle je suppose que la vitesse de la lumière est différente dans l' aller et dans le retour : merci de répondre à mes questions !le lien https://forums.futura-sciences.com/p...-einstein.html

Cette "démonstration" est :
- non conforme au point 6 de la charte
- dans la discussion que vous indiquez, les erreurs ont été soulevées
- c'est HS ici.

et vous pouvez avoir le niveau que vous prétendez avoir, plusieurs des intervenants qui vous ont répondu ne sont pas des ignares non plus, loin de là...

Pour la modération,

[invite9dc7b526]

@1max2: le cercle est un cas particulier de conique et je pense que tu trouverais plus d'informations si tu cherchais les propriétés des coniques. Regarde en particulier les théorèmes d'Apollonius.

[1max2]

Pardon, mais j' ai pris le résultat admis par tous pour C+ et C- et j' ai remarqué que la vitesse moyenne(valable pour une voiture aussi ) sur un aller-retour n 'est pas (C(t+) + C(t-))/2 mais (2C(t+) x C(t-))/(C(t+) + C(t-))
ET........si l'on calcule la vitesse moyenne sur cet "aller-retour" , devinez ce que l'on trouve ? ...On trouve c , vitesse de la lumière dans le vide .(2C(t+) x C(t-))/(C(t+) + C(t-))=c !!
C'est la même chose pour un Sagnac avec fibre d'indice n
V(t+)=(c²-v²)/(nc+v)
V(t-)=(c²-v²)/(nc-v).............la vitesse moyenne devient ....c/n !
Personne ne m' a contredit là dessus, vu que j' ai pris les résultats admis dans le repère tournant ! Sur Terre quand on envoie un faisceau lumineux à l' ouest et un à l' Est en même temps et sur le même parcours(distance), le faisceau qui va dans le sens de rotation arrive après, c'est l' effet Sagnac, on est bien obligé d' admettre que dans le repère tournant Terre la lumière va plus vite d'un côté .Ce que j' ai trouvé (et sans doute d' autres aussi, mais moi je n' en ai jamais entendu parler ) c'est que la moyenne des vitesses"apparentes" vers l' est et vers l'ouest donne c dans le vide et c/n dans la fibre , c'est un résultat remarquable !
J' ai pris congé un certain temps du forum, et j' ai publié ici un résultat de géométrie élémentaire que je ne connaissais pas, mais que je soupçonnais ...
ggO s'est moqué de moi, c'est son droit tant que c'est correct, un autre prétend que c'est connu depuis 2500 ans, je veux bien le croire c'est probable, mais il ne m' a pas donné de précision ni de lien .. Je suis certain par contre que cette propriété est connue, mais je ne l' ai jamais vue ! Je n' ai aucune prétention !Mon but était de poser la démo quelque part pour laisser une trace .
Je suis certain que ce serait utile de mettre cette propriété au programme de 3 ème car c'est en fait une propriété plus générale de 2 droites sécantes coupant un cercle, ! Le cas particulier connu est celui où les 2 droites se coupent sur le cercle !
Non, je ne m' appelle pas Sagnac
Minushaben, merci pour l'info j' irais voir du côté des coniques, par contre je connaissais le théorème d' Apollonius.

[danyvio]

Je ne sais pas si les notions d'angle inscrit, arc capable etc. étaient connues il y a 2500 ans, mais elles étaient connues des marins. Ils pouvaient faire le point en mesurant l'angle sous lequel ils voyaient deux phares ( ou d'autres amers). Connaissant cet angle, par une construction géométrique "élémentaire" mon cher Imax2, ils traçaient sur la carte LE cercle sur lequel ils étaient susceptibles de se trouver. A défaut d'un troisième amer, ils avaient toujours le pôle nord pour construire un deuxième cercle coupant le premier au bon endroit.

[1max2]

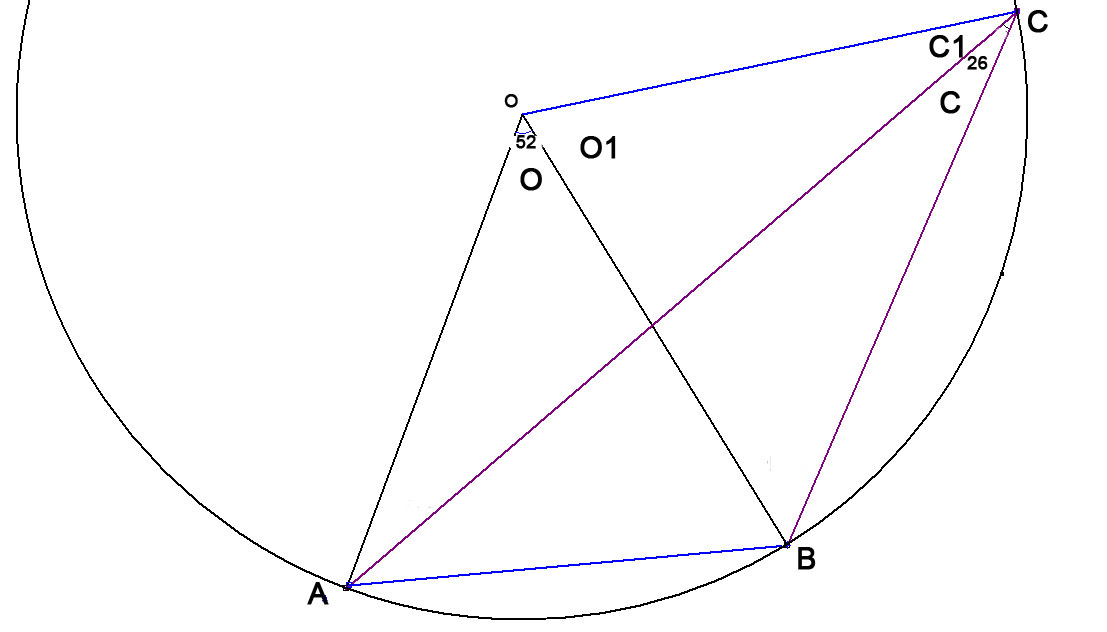Très très intéressant , je cherchais justement à quoi pouvait servir cette propriété, mais si j' ai bien compris en regardant l' angle qu'ils faisaient avec le phare ils pouvaient tracer le cercle, et c'est donc la propriété connue qu'ils employaient celle des arcs capables, quand l'intersection des droites se situe sur le cercle .Ce n'est pas cette propriété dont je parle c'est une propriété plus générale, j' espère que vous l ' avez compris !
Il avaient donc le nord et pouvaient alors tracer une droite et se situer sur ce cercle, c'est effectivement intéressant , je ne connaissais pas, vous avez un lien internet ?

[invitedd63ac7a]

Je ne sais pas si les notions d'angle inscrit, arc capable etc. étaient connues il y a 2500 ans,

D'accord, je fais amende honorable, je ne sais pas si cela était connu il y a 2500 ans, mais il y a 2300 ans Euclide connaissait ces notions puisqu'elles sont traitées dans le Livre III des Eléments. Désolé pour l'erreur de 2 siècles.

[1max2]

Merci du lien, très intéressant, j' ai lu assez rapidement j' avouemais Euclide parle effectivement selon wikipédia (que chacun peut modifier contrairement à la bible )
Je note Angle au centre et angles inscrits :" La prop.20 prouve que l'angle au centre est le double de l'angle inscrit correspondant. La prop.21, généralisée dans les prop.26 à 29, prouve que des angles inscrits interceptant le même arc sont égaux et réciproquement. La prop.22 prouve que les angles opposés d'un quadrilatère inscrit dans un cercle sont égaux à deux droits.
Propriété des segments de cercle. Les prop.23 à 25 traitent des segments de cercle. Par exemple, un segment étant donné, la prop.25 décrit le cercle dont il est le segment. Les prop.33 et 34 donnent des constructions relatives aux segments de cercle."
J' ai peur que vous n' ayez pas bien compris le sujet de mon post, pour moi les droites se croisent à un point quelconque du cercle, et non au centre ou sur le cercle avez-vous compris cela ? je peux me tromper évidemment ! Euclide ne parle pas selon wikipédia d'un point quelconque du cercle, qui est le sujet de mon post, sauf erreur de ma part !

[invitedd63ac7a]

Je citais les Elements d'euclide en réponse á l'interrogation de Danyvio. Je n'ai pas dit que votre propriété était citée dedans. Sans dénigrer votre travail qui reste intéressant et louable car il peut constituer un bon exercice dans un problème à donner à des élèves. Il fait référence à une propriété géométrique parmi une infinité d'autres qui peuvent être trouvées. Par exemple, pensez aux polygones à n côtés inscrits dans un cercle pour n valeur entière quelconques >2. On peut exhiber à partir de ces derniers de multiples propriétés, selon les contraintes que vous leur appliquerez. Certaines seront inintéressantes, d'autres paraitront étonnantes. Tels ce polygone régulier à 17 côtés constructible exactement (Gauss) à la règle et au compas. Alors que ceux qui précèdent ne le peuvent pas, sauf pour 3,4,5,6,8,10,12,16.

[Resartus]

Bonjour,
Quelques secondes de recherche internet donnent ceci : (vers le milieu de la page)
http://www.alloprof.qc.ca/BV/Pages/m1297.aspx

Mais il est en effet probable que la géométrie élémentaire disparait plus rapidement en France qu'au Canada…

[1max2]

Oui effectivement, merci pour le lien c'est cette propriété, je ne la connaissais pas ! Il me semble l' avoir souvent croisée dans certains problèmes, et je suis certain que si je l ' avais connue et pu l'employer beaucoup de problèmes auraient été plus simples à résoudre !Ce qui m ' a étonné c'est de ne pas avoir appris cette propriété alors qu'elle me semble assez élémentaire, et que le cas où le point de croisement des droites se trouve sur le cercle n'est qu'un cas particulier en fait !

[1max2]

Voilà , j' ai retrouvé: sur facebook, un ami me demande de trouver la solution pour démontrer que GHI sont alignés , je me suis servi de cette propriété que j' ai du évidemment démontrer

[invitedd63ac7a]

Je voudrait préciser le sens du mot élémentaire que j’utilise régulièrement dans un sens bien précis. Les mathématiques élémentaires, ce sont les mathématiques que l’on enseigne, dans le secondaire, c’est à dire au lycée et au collège. Cela correspond, aux premiers livres des Eléments d’Euclide (je fais référence à Euclide car jusque dans les années 1970, les programmes de géométrie du secondaire étaient basée sur les premiers livres des Eléments). Attention, mathématiques élémentaires n’est en rien péjoratif, des exercices de mathématiques élémentaires peuvent être très compliqués, car ils utilisent nécessairement et seulement les théorèmes du Collège-Lycée.

[invitedd63ac7a]

@imax2
La figure de votre message #22 illustre une jolie propriété de géométrie projective: elle est vraie pour les coniques d'une façon générale, mais on la retrouve encore en remplaçant le cercle par deux droites quelconque du plan (conique dégénérée, sauf erreur).
Construisez votre figure en fil de fer, mettez la au soleil (ou derrière une lampe ponctuelle), son ombre est une conique (ellipse, parabole hyperbole) et la propriété demeure...

[1max2]

@imax2
La figure de votre message #22 illustre une jolie propriété de géométrie projective: elle est vraie pour les coniques d'une façon générale, mais on la retrouve encore en remplaçant le cercle par deux droites quelconque du plan (conique dégénérée, sauf erreur).
Construisez votre figure en fil de fer, mettez la au soleil (ou derrière une lampe ponctuelle), son ombre est une conique (ellipse, parabole hyperbole) et la propriété demeure...

Vous voulez dire que les points ABC et DEF peuvent se trouver sur 2 droites ABC sur l'une et DEF sur l'autre, mais ce n'est pas le théorème de Desargues ça ? C'est assez loin pour moi, je me souviens Desargue se démontrait assez facilement en 3 D mais j' ai buté sur la démo en 2 D, et ça me fait penser à une propriété que j' ai lue sur un livre de Feynman effectivement qui remplaçait l' ellipse de l' orbite par une droite et on avait le même résultat .......Je vais me pencher là dessus ...