Dm dérivées exponentielles

[Lucas34200]

Bonsoir à tous j'ai un dm à réaliser et je coince un peu si vous pourriez m'aider ça serait sympa
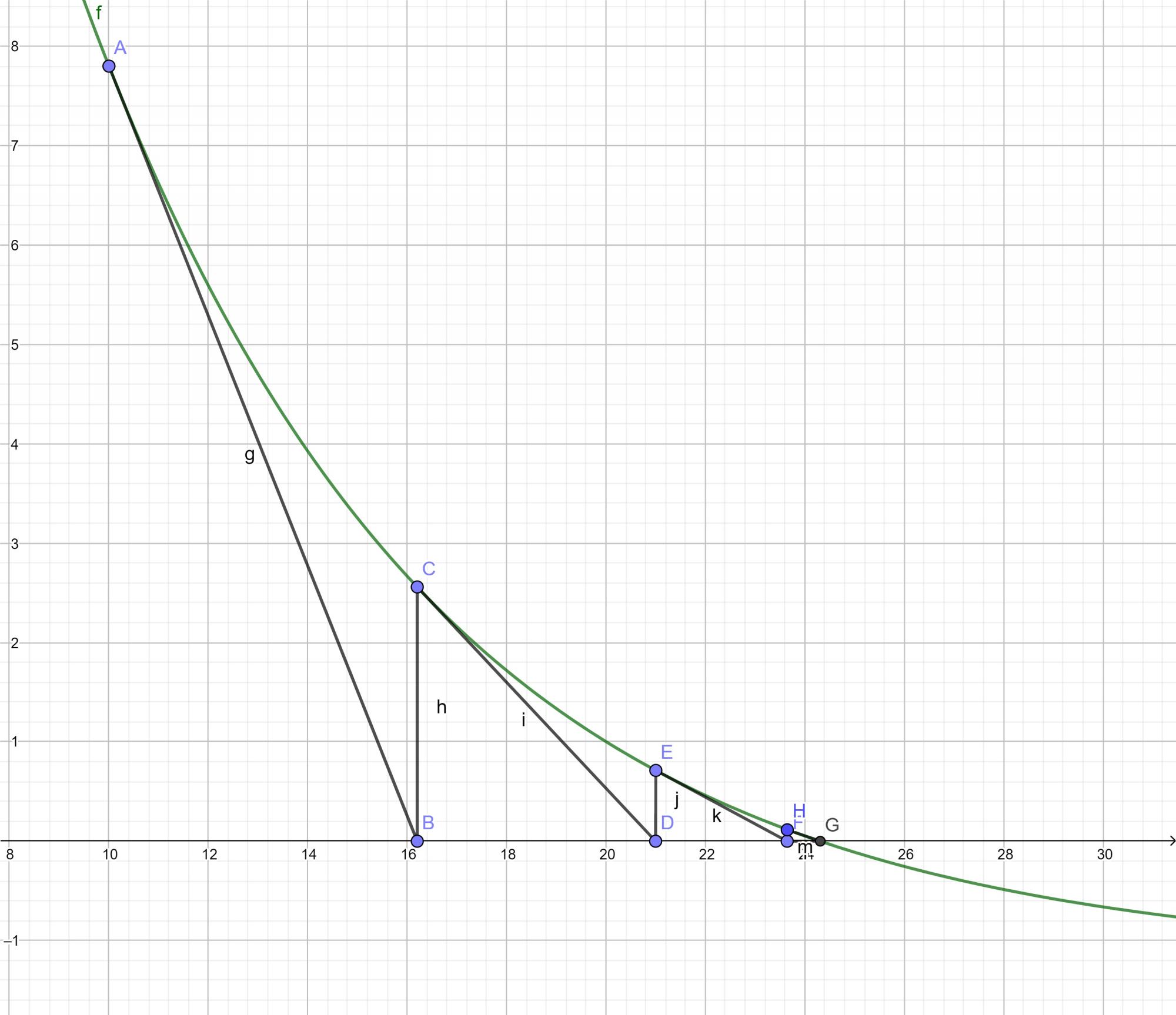
La toiture d'une salle de sport a un profil représenté ci contre
Ce profil est modélisé par la fonction : f1(x) = -0,09x^2+ 0 ,04x + 16,4 sur [0;10]
f2(x) = 12e^(-0,14077x+1,12) - 1,2 sur [10 ; +infini [
1 ) Etudier la continuité de la courbe de la toiture au point d'abscisse 10

2 ) Déterminer les expressions des dérivées de f à gauche et à droite de 10. f est-elle dérivable en 10 ?
Pour des raisons de faisabilité l'écart entre les deux tangentes ne doit pas être supérieur à 10%. Cette conditions est-elle respectée ?

3 ) La pente de la courbe ne doit pas excéder en pourcentage 200% pour que le revêtement ne se détache pas trop facilement . Cette courbe respecte-t-elle cette condition ?
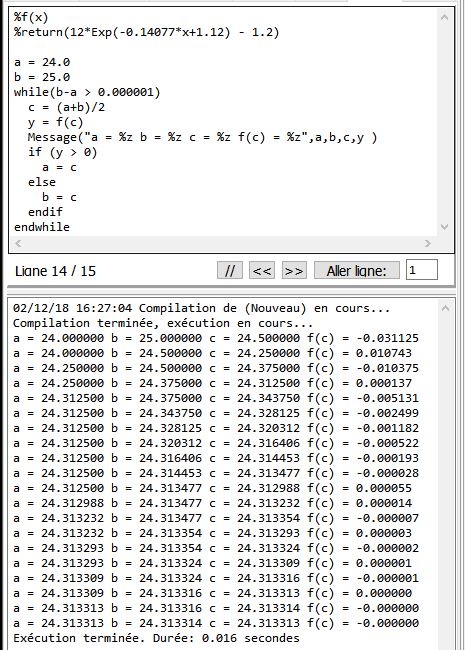
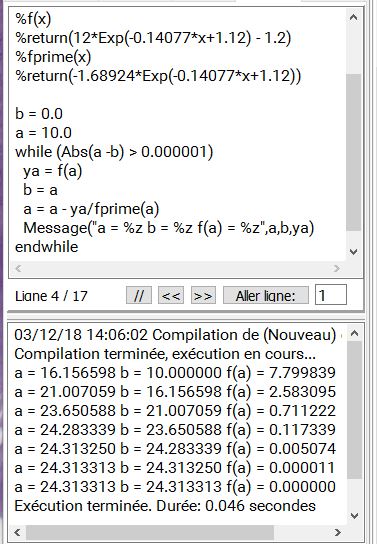
4 ) Ecrire un algorithme qui permette de determiner l'abscisse du point C de contact avec le sol . Donner une valeur approchée au centième près de cette abscisse

Une fonction est continue en un point lorsque lim f(x) ( quand x tend vers a ) = f(a) f1(x) = 7,8 et f2(10 ) = 7,79 La fonction n'est donc pas continue en 10
2 ) f'1(x) = -0,18x +0,04
f'2(x) = -0,14077 x 12e^(-0,14077x+1,12 )
Pour f1(10) y = -1,76x+ 25,4 , pour f2(10 ) y =-1,26 x +20,39 comme l'écart entre le coefficient de la tangente de f1(10 ) et de f2(10 est de 50% alors la condition n'est pas respectée
3) je sais que les coefficients directeurs des tangentes ne doivent pas dépasser 2 en valeur absolue et que je dois encadrer tous les nombres dérivés et montrer qu'ils sont compris entre -2 et 2
jai étudié les variations de mes 2 fonctions mais à aucun moment j'ai trouvé des résultats entre 2 et - 2
4) je sais que l'on doit utiliser l'algorithme de dichotomie et que C est censé être le milieu de f1(x) et f2(x) mais quels sont les deux valeurs que je dois prendre pour a et b pour effectuer et créer l'algorithme ? je vous remercie d'avance de vos reponses
-----

[ansset]

bjr,
concernant la 3), il est facile de montrer que |f'1(x)|<2
quand à f'2(x) c'est une fonction strictement décroissante en valeur absolue donc il suffit de montrer que |f'2(10)|<2
concernant la 4, on attend peut être de toi un algorithme "à la Newton" concernant la fonction f2.
à savoir par projection successive de la tangente en un point de la courbe sur l'axe des abscisses, ce qui donne une autre abscisse et une autre tangente. ( possibilité d'explication plus complète si nécessaire )


ps: je ne comprend pas cette histoire de "milieu" des deux fonctions.
pour ma part , le résultat est de l'ordre de 24.

ps2, les fonctions ne sont effectivement pas contnues en x=10, mais l'écart est bien plus faible que ce que tu présentes ( env 1,6 10^(-4))

[Lucas34200]

Bonsoir merci de votre réponse alors j'ai calculé f'2(10) et ait obtenu -1,26 qui est bien inférieur à 2 en valeur absolue et pour f'1(10 ) j'ai -1,76 donc la condition est bien respectée car les deux resultats sont inférieurs à 2 en valeur absolue
4 ) là j'ai vraiment pas compris ce que vous avez dit , je vois juste que le point d'abscisse C est compris entre 24 et 25 graphiquement mais je sais pas comment établir l'algorithme et non plus le langage
pour l'écart en effet faute d'étourderie de ma part dans les calculs

[ansset]

le principe est le suivant , on part d'un point sur la courbe de f2 , par exemple (10,f2(10))
la tangente à cette courbe en ce point (x0,f2(x0)) vaut
T0(x)=f2(x0)+(x-x0)f'2(x0)
On cherche l'intersection de cette tangente avec l'axe des abscisses, soit quand T0(x1)=0
Ce qui donne un point d’abscisse x1 qui vérifie
x1=x0-f(x0)/f'(x0)
et on recommence avec un nouveau point sur la courbe (x1,f2(x1))
cette suite converge très vite vers le point ou f2(x)=0. ( à 10^(-n) prêt )
tu peut le faire par programme ou tout simplement sur excel.

désolé de ne pas joindre un graphique ( suis nul avec géogébra )

[A voir en vidéo sur Futura]

[ansset]

En partant de x0=10,
les valeurs successives obtenues sont
16,156....
21,007....
23,650....
24,283....
24,31325
24,3133132 pour lequel f2(x)=0 ( à 4 10^(-11) prêt)

[Lucas34200]

bjr merci de la reponse Mathématiquement je vois le raisonnement mais au niveau algorithme je suis vraiment nul jai vu plusieurs différents algorithme concernant dichotomie mais je sais pad lequel utiliser , jai pense à un algorithme de balayage tant que f(x) >0 on incrémente de 0.01 et je prends a et b qui sont respectivement 24 et 25vmais apres je sais pas comment faire et rediger correctement

[ansset]

Il est certainement probable qu'il est attendu un raisonnement par dichotomie.(*)
dans ce cas , on peut constater graphiquement que f(x)=0 pour x0=24<x<x1=25
avec f(24)>0 et f(25)<0
algo possible
calculer f(x3) avec x3=(x1+x2)/2)=24,5
si f(x3)>0 prendre x4=(x3+x2)/2
sinon prendre x4=(x3+x1)/2
etc....
prendre à chaque fois le milieu entre la dernière abscisse où f(x) >0 et celle ou elle est négative.

la méthode que j'ai suggéré est plus générale et "va plus vite", mais n'est certainement pas enseignée en 1ere.
j'essayerai quand même de faire un schéma dans la journée.

[jacknicklaus]

bjr merci de la reponse Mathématiquement je vois le raisonnement mais au niveau algorithme je suis vraiment nul jai vu plusieurs différents algorithme concernant dichotomie mais je sais pad lequel utiliser , jai pense à un algorithme de balayage tant que f(x) >0 on incrémente de 0.01 et je prends a et b qui sont respectivement 24 et 25vmais apres je sais pas comment faire et rediger correctement

voir ici : https://forums.futura-sciences.com/m...ml#post6261158

attention, faudra peut-être modifier, dans le post donné en exemple, on avait une fonction croissante dans l'intervalle initial [1,2]. Faut inverser le choix "a=c" et "b=c" si c'est décroissant dans l'intervalle.

[Lucas34200]

merci de vos réponses alors jai réalisé un algo mais je sais pas si c'est correct
f(x)=12e^(-0.14077x+1.12)
a=24
b=25
Boucle x fois
c=(a+b)/2
y= f(c)
tant que f(x)>0
on incrémente d'un pas de 0 01
si y>0 b=c
sinon a=c
Fin boucle

[ansset]

non, il ne peut marcher tel qu'écrit, car f(24,5)<0
donc tu ne peux incrémenter ( en augmentant ) à partir de cette valeur.

[ansset]

En fait , l'idée est d'avantage de redéfinir a ET b, en fct de f(c)

[ansset]

plus clairement,
soit tu incrémente avec un petit pas à partir de 24, mais ce n'est pas un algo par dichotomie.
soit tu recherches à chaque fois une valeur intermédiaire en fct des résultats précédents.
ici, j'ai l'impression que tu veux faire les deux en même temps , confusion !

[Lucas34200]

si je prends a=24 et b =24.5 mon algorithme marchera ?

[ansset]

lequel, car tu mélanges une incrémentation avec une dichotomie !
Il faut faire un choix !
et tu oublies ( si tu optes pour une dichotomie ) qu'il te faut un résultat à 1% prêt.

[ansset]

quel algo ?
si tu veux faire une dichotomie , il suffit de s'inspirer du post #8 ( de Jack ).
mais dans ce cas, il faut aussi tenir compte qu'on te demande une valeur approchée à 10^(-2) prêt.
donc finir la boucle quand (b-a)<0,01 par exemple et non sur un nb arbitraire d'itérations.
(a, b et donc c évoluant à chaque itération )

Tu peux aussi faire une incrémentation d'un eps choisi ( mais c'est plus "bourrin" ) à partir de 24. et t’arrêter dès que f(x)<0.
Mais pas les deux en même temps.

pardon pour le double post, mais l'ancien n'apparaissait plus !!!! ?????

[Lucas34200]

Je pense que je vais opter pour l'algo avec incrémentation mais pourriez vous m'aider à le réaliser pour dichotomie vous m'avez donné un exemple mais pour incrémentation non et j'en ai pas fait encore en classe

[ansset]

que n'as tu pas fait en classe.?
sinon , les deux méthodes ont été expliquées, qu'est ce qui coince ?
pour la dichotomie, il suffit d'adapter le post de jack.
pour l'incrémentation avec un "petit pas", c'est évident, non ?

[ansset]

sinon, mais c'est plus pour la culture générale, la méthode avec les tangentes ressemble à ça :
je reposterais ( image non-valide )

[jacknicklaus]

Je pense que je vais opter pour l'algo avec incrémentation mais pourriez vous m'aider à le réaliser pour dichotomie vous m'avez donné un exemple mais pour incrémentation non et j'en ai pas fait encore en classe

je crois que le petit langage utilisé est suffisamment évident à lire pour me dispenser de commentaires.

[ansset]

nouvel essai :

[ansset]

pour le reste, rien à ajouter au post de Jack.
l'algo ( dichotomique ) est très facilement compréhensible.
quand à ma figure, c'est uniquement pour montrer qu'il existe d'autres solutions.
( plus complexes mais parfois très efficaces )
ne pas en tenir compte ici, vu les difficultés que tu rencontres

[Lucas34200]

Merci beaucoup , je crois que j'y serais jamais arrive sans votre aide parce que j'étais complètement paumé au sujet de cet algorithme et je voudrai juste avoir une petite précision j'ai étudié les variations de la 2eme fonction f'2(x) qui est au negative donc décroissante en la redérivant pour savoir si f'2 (x) était croissante ou décroissante et j'ai obtenu f''2(x) = 0,23 e^(-0,14077x+1,12) qui est de signe positif donc au final f'2 ( x) sera croissante ou décroissante ?

[ansset]

bon reprenons....
f'2(x) est décroissante, mais ce n'est pas ce qui importe le plus.

reprenons l’algorithme par dichotomie entre24 et 25
on sait que que la solution se trouve entre les deux et que l'on souhaite une valeur à 0,01 prêt.
l'intervalle initial est ente 24 et25.
donc a=24 et b=25
et f2(a)>0 et f2(b)<0
le but du "jeu" est de réduire au max cet intevalle
sot c=(a+b)/2
soit f(c)>0 auquel cas le chiffre cherché est entre c et b
dans ce cas on remplace a par c et on reprend l'intervalle entre le nouveau a et b inchangé
soit f(c)<0 auquel cas le chiffre cherché est entre a et c
dans ce cas on remplace b par c et on reprend l'intervalle entre le nouveau b et a inchangé

peut être qu'un dessin te serait plus parlant.

à chaque fois l'intervalle se réduit.
et on arrête dès que les nouveaux b-c <0,01

comprends tu le principe. ??

[Lucas34200]

oui jai réussi à comprendre le systeme et là f(c) <0 donc la valeur de notre point se situe entre a et c puis ensuite on a mis la valeur trouve a la place de b puis on fait de nouveau tourner l algo et ainsi de suite jusqu'à f(c) =0
mais pour calculer les limites aux bornes de f'2(x) je dois rederiver et là j obtiens une fonction croissante pour f'2(x) dokc je suis 1 peu perdu

[ansset]

1) oublie la dérivée de f2 ici. elle est inutile.(*)
2) on ne cherche pas c tel que f2(c)=0, mais une valeur approchée à 1/100 ème prêt.
il suffit pour cela d’arrêter la boucle quand les derniers (b-a)<0,01.

(*) ici , je ne m'en servais que pour l'optimisation "à la Newton" que j'avais proposé pour la "culture générale", mais qui n'est probablement pas apprise en 1ère. ( donc à oublier ), et qui n'a rien à voir avec l'approche dichotomique.

ps; on ne change pas forcement a par c, puis b par c systématiquement, tout dépend à chaque itération de la valeur de f(c).

[Lucas34200]

désolé de m'être mal exprimé mais je parlais de la question 3 et du calcul de la dérivé de f'2(x) qui est une fonction décroissante par méthode calculatoire mais croissante dans les négatifs à la calculette alors j'ai un doute
Ok j'essaye de le réaliser dans l'après midi tout en m'aidant du modèle apporté plus haut par monsieur jacknicklaus et en l'adaptant à mon exo

[jacknicklaus]

La méthode de Newton, dont on voit bien qu'elle est bien plus rapide que la dichotomie (7 étapes pour obtenir 24.313313 et 20 étapes pour la dichotomie)

A titre exercice; essaye de retrouver la formule "a - ya/fprime(a)" qui donne la coordonnée x où la droite , qui passe par le point (a,f(a)) et dont la pente en cet endroit est f'(a), coupe l'axe y = 0. cf graphique d'ansset

 Cliquez pour afficher

[gg0]

désolé de m'être mal exprimé mais je parlais de la question 3 et du calcul de la dérivé de f'2(x) qui est une fonction décroissante par méthode calculatoire mais croissante dans les négatifs à la calculette alors j'ai un doute
Ok j'essaye de le réaliser dans l'après midi tout en m'aidant du modèle apporté plus haut par monsieur jacknicklaus et en l'adaptant à mon exo

Rappel :
"f2(x) = 12e^(-0,14077x+1,12) - 1,2 sur [10 ; +infini ["
parler de f2 "dans les négatifs n'a aucun sens !!
D'autre part, tu parles de "de la dérivé de f'2(x)" alors qu'il s'agit plus probablement de f'2, pas de sa dérivée. de la dérivée de f2.

Attention à ce que tu fais (rester dans l'énoncé) et à ce que tu écris.

Cordialement.

[ansset]

La méthode de Newton, dont on voit bien qu'elle est bien plus rapide que la dichotomie (7 étapes pour obtenir 24.313313 et 20 étapes pour la dichotomie)

et encore, c'est parce que je suis parti du début de la courbe ( x=10)
en partant ( comme la dichotomie ) de 14, il suffit de 3 itérations pour aboutir à un résultat < 1/100

[ansset]

erratum, en partant de x=24 c'est encore bien plus court.