Bonjour,
Je ne comprend pas comment je peux réussir à poser mes intégrales pour trouver la hauteur de l'eau dans le problème suivant.
Une sphère de 8 cm de rayon se trouve à l'intérieur d'une seconde sphère de 13 cm de rayon, qui contient une certaine quantité d'eau. La coupe transversale ci-contre indique le niveau d'eau. Déterminer la hauteur de l'eau dans la grande sphère lorsque l'on retire la petite sphère. (La petite sphère touche dans le fond de la grande sphère).
Dois-je utiliser la méthode des disques, des disques troués, des tubes ? Comment dois-je m'y prendre. Merci d'avance.
Chris Cooper
-----





 ( ou r est dépendant de la hauteur h' comprise entre R-h et R )
( ou r est dépendant de la hauteur h' comprise entre R-h et R )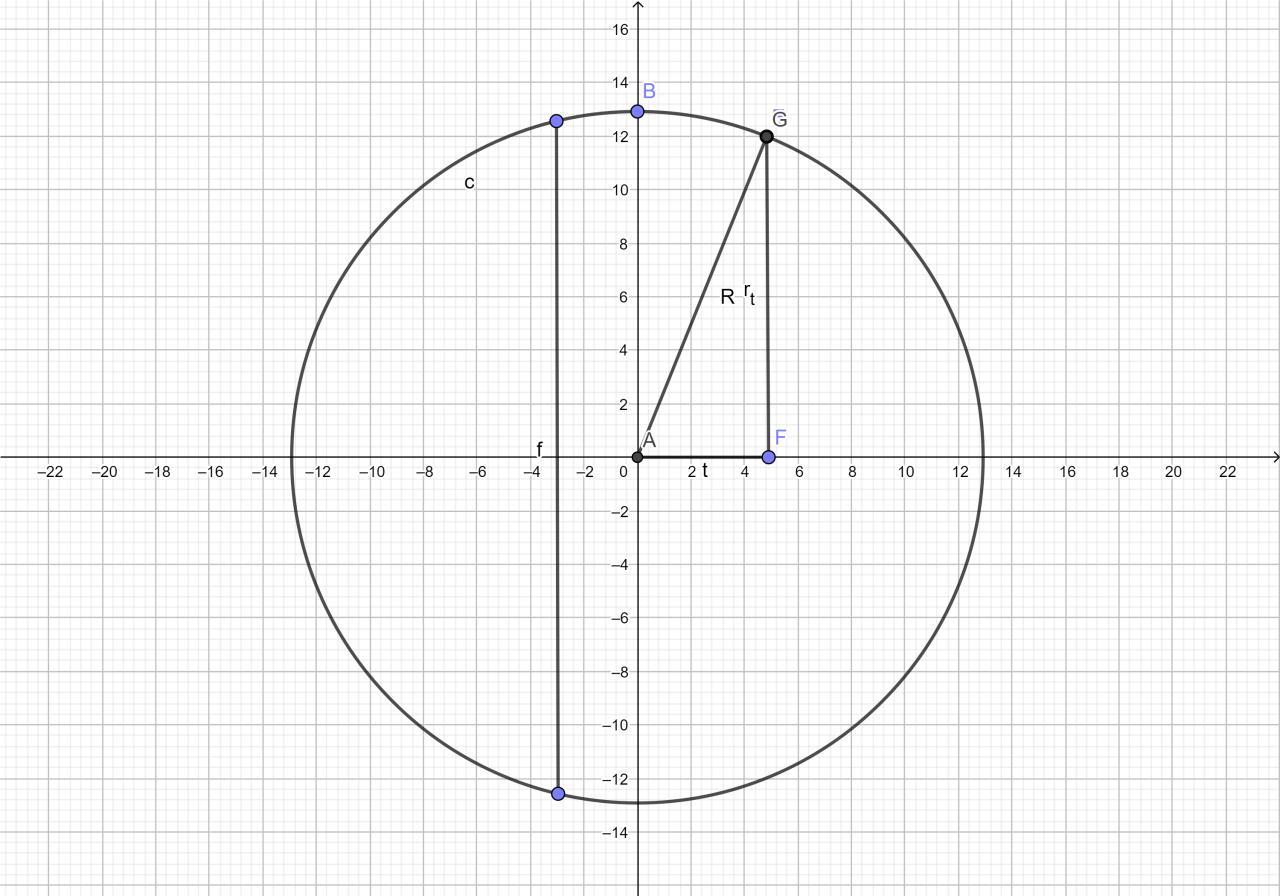 une image pour être plus clair.
une image pour être plus clair.