Les coniques

[Yvan_Delaserge]

Bonjour,

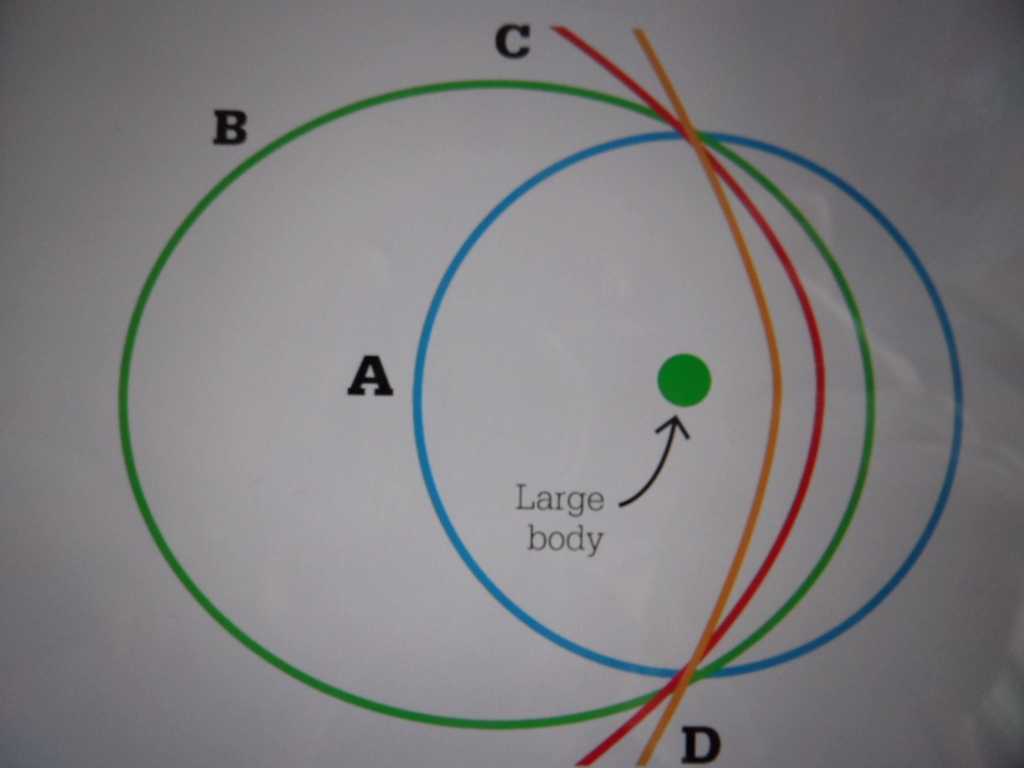
On sait que les coniques sont de quatre types: cercle (A), ellipse (B), parabole (C), hyperbole (D).



Ces quatre courbes se caractérisent par leur excentricité. Si elle est de:
0: C'est un cercle.
>0, mais <1: C'est une ellipse.
1: C'est une parabole.
>1: C'est une hyperbole.

Sur le dessin, on voit que toutes ces courbes passent( à peu près mais admettons que ce soit bien le cas) par les deux mêmes points.

Ma question est la suivante: Est-il vrai que:
S'il s'agit d'un cercle, on ne peut faire passer que deux cercles par ces deux points. Un qui se trouvera à gauche et un à droite, sur le dessin ci-dessus.
Même chose pour une parabole.

Par contre, pour une ellipse ou pour une hyperbole, on aura une infinité de possibilités.

Cette affirmation vous paraît-elle correcte?

Merci d'avance.
-----

[gg0]

Bonjour.

Soient A et B deux points distincts. Pour tout point O de la médiatrice du segment [AB], le cercle de centre O et de rayon OA passe par A et B.
par contre, si le rayon est fixé, et strictement supérieur à AB/2, il existe deux cercles de ce rayon passant par A et B, dont les centres sont symétriques par rapport à la droite (AB).

Une remarque : En général, on rajoute à tes quatre cas trois cas dégénérés : deux droites, une droite (dite double) et un point. Ce qui épuise les cas possible, que la définition soit géométrique (intersections d'un plan avec un cône) ou analytique (courbes non vides d'équations ax²+by²+cxy+dx+ey+f=0, avec au moins l'un des coefficients a, b et c non nul. le cercle est le cas a=b non nul, c=0).

Cordialement.

[Yvan_Delaserge]

Bonjour gg0 et merci de votre réponse.

Une droite passant par les deux points équivaudrait je pense à une hyperbole d'excentricité infinie.
Donc il existe une infinité d'hyperboles possibles passant par les deux points?

Amicalement,

[gg0]

Oui,

une hyperbole limite, ou un cercle limite, ou une parabole limite, etc.
Et par deux points passent une infinité d'hyperboles (même si on impose que les points soient sur la même branche), de paraboles, d'ellipses, ...

[A voir en vidéo sur Futura]

[Yvan_Delaserge]

Oui bien sûr. Par deux points on peut faire passer une infinité de toutes les coniques. C'est moi qui ai mal posé le problème, désolé.
C'est parce que je ne voyais qu'une partie de l'espace, là où x et y sont positifs.



Les deux points dont je parlais sont l'origine et le point tout à droite, de coordonnées x;y = 700;200.

Combien de cercles, ellipses, paraboles, hyperboles, peut-on faire passer par ces deux points, en posant comme conditions:
a) qu'elles doivent être symétriques par rapport à l'axe y.
b) qu'elles doivent être tangentes à l'axe x, au point 0;0.
c) que les valeurs de y de tous les points de ces courbes doivent être positives.

Les équations des trois courbes sont les suivantes:
parabole: y= c*x^2
cercle: y= r- racine (r^2 - x^2) où r est le rayon.
hyperbole: y=racine (a^2(1+(x^2/b^2))) -a

Si on veut que la parabole ou le cercle passent par les deux points, une seule valeur de c, respectivement de r, pourra aboutir à ce résultat.
Alors que pour l'hyperbole, on peut y arriver avec une infinité de combinaisons de a et b, chaque combinaison donnant une courbe différente.

[gg0]

Rien à voir avec ta question initiale !!!

Par exemple, pour ta parabole, tu n'as pas choisi une parabole quelconque passant par O et M, mais encore une parabole de sommet O; ce qui change tout !!

[gg0]

Par contre, tu laisse bien plus de liberté à ton hyperbole.

Et comme finalement, c'est toi qui décides du sens des mots, je ne vois plus d'utilité à répondre à des questions piégées.

[Yvan_Delaserge]

Bonsoir gg0.
Tu as raison, ma question initiale était mal posée.
Mais es-tu d'accord avec mon raisonnement de la fin du message #5?
Merci d'avance car un regard extérieur et informé est précieux, pour moi.

[gg0]

Vu que tu imposes dans l'équation que la parabole passe par O et qu'il y a un seul paramètre, il est facile de le déterminer avec l'autre point (s'il n'est pas sur l'axe des y); idem pour le cercle (si le deuxième point est dans le premier quadrant).
Mais ça ne s'oppose en rien au cas de l'hyperbole, puisque tu as justement choisi une équation avec deux paramètres.
Tu fabriques une opposition qui n'a rien à voir avec la nature des courbes.

A noter : Il y a bien d'autres types d'équations possibles pour ces trois courbes.

[Yvan_Delaserge]

Bonsoir gg0 et merci de ta réponse.
Tu veux dire qu'il existe d'autres équations pour une courbe hyperbolique, passant par 0;0 et symetrique par rapport à l'axe y?

[Yvan_Delaserge]

Je pose mes questions peut-être un peu maladroitement et je conçois qu'il peut être agaçant pour celui qui les lit de se demander "mais ou veut-il en venir?"
J'explique donc pourquoi je pose ces questions.
J'aimerais savoir si la surface d'un reflecteur parabolique rond, de diamètre et de profondeur connues, ne peut avoir qu'une seule et unique forme.
Même question si la surface du réflecteur est sphérique.
Même question si elle est hyperbolique.

[gg0]

Tout est dans la définition des quantités mesurées.
Je suppose qu'il s'agit à chaque fois de surfaces de révolution autour d'un axe sur lequel tu fais la mesure de la "profondeur". le bord de ton réflecteur est donc un cercle, dans un plan perpendiculaire à l'axe. Et c'est la diamètre de ce cercle que tu appelles le diamètre du réflecteur. le problème se ramène alors à un problème plan en coupant par un plan contenant l'axe, et même à un demi-plan puisqu'une rotation de 180° autour de l'axe ramène la courbe d'un côté à celle qui est dans l'autre demi-plan. Et donc, avec un repère adapté, à la détermination des courbes (parabole, cercle, hyperbole) passant par l'origine, avec tangente horizontale, et par le point de coordonnées (demi-diamètre, profondeur).
Pour parabole et cercle, il est effectivement raisonnable de prendre les équations que tu cites. Les paraboles sont toutes de même forme (par translation, rotation et homothétie, on passe de n'importe quelle parabole à n'importe quelle autre); idem pour les cercles. Par contre, les hyperboles (comme les ellipses, sont toutes de formes différentes. Donc tes données (profondeur et diamètre) ne définissent pas une hyperbole. Il manque disons l'angle entre les asymptotes à l'hyperbole.
Dans ce sens là, il y a bien une infinité d'hyperboles possibles.

Cordialement.

NB : Dommage que tu n'aies pas commencé par cette explication.

[Yvan_Delaserge]

Super. Merci gg0. Voilà qui répond parfaitement à ma question.
On ne sait jamais comment faire pour bien faire. Faut-il exposer sa question brute de décoffrage au risque de passer pour quelqu'un qui attend qu'on fasse tout le travail pour lui?
Ou bien faut-il tenter d'exposer le problème en termes mathématiques? On est sur un forum de mathématiques après tout!
Encore une fois merci. Il est probable que j'aie encore quelques questions prochainement. Ce que je cherche a faire est simple à enoncer: Transformer une antenne parabolique à un seul réflecteur en antenne Cassegrain. Vaste programme.

[albanxiii]

Bonjour,

On ne sait jamais comment faire pour bien faire. Faut-il exposer sa question brute de décoffrage au risque de passer pour quelqu'un qui attend qu'on fasse tout le travail pour lui?

Comme vous avez fait là :

Je pose mes questions peut-être un peu maladroitement et je conçois qu'il peut être agaçant pour celui qui les lit de se demander "mais ou veut-il en venir?"
J'explique donc pourquoi je pose ces questions.

ça me semble la bonne démarche. Au besoin précisez que vous n'êtes pas un étudiant qui a un exercice à faire.

[gg0]

Bonjour Yvan.

Il aurait été plus clair que tu exposes à la fois ton but (le réflecteur - message #11) et tes préoccupations mathématiques. A la lecture de ton premier message, on était bien loin de ce que tu as fini par préciser. Résultat, j'ai répondu exactement à ce qui était écrit, pas à ce que tu voulais savoir.
Sur une question de maths, on fait des maths; sur une question de maths appliquées, on fait de l'application des maths.

Cordialement.