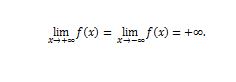Bonjour tout le monde,
Veuillez bien m'aider avec cet exercice;
Soit f une fonction dérivable sur R telle que;
Montrer qu'il existe a de R*- et b de R*+ tels que :
f(a) > f(0) + 1 et f(b)> f(0) + 1
j' ai essayé de considérer la fonction g(x)= f(x)-(f(0)+1) et de raisonner par absurde sans succès.
Merci d'avance!
Bonjour.
Il suffit d'appliquer les définitions des limites à l'infini en utilisant f(0)+1; éventuellement en imposant les signes pour a et b.
Par exemple que donne
Cordialement
Bonjour
1 - montrer que f(0) existe
2 - écrire la contraposée de
3 - comparer avec la définition de
4 - conclure
There are more things in heaven and earth, Horatio, Than are dreamt of in your philosophy.
