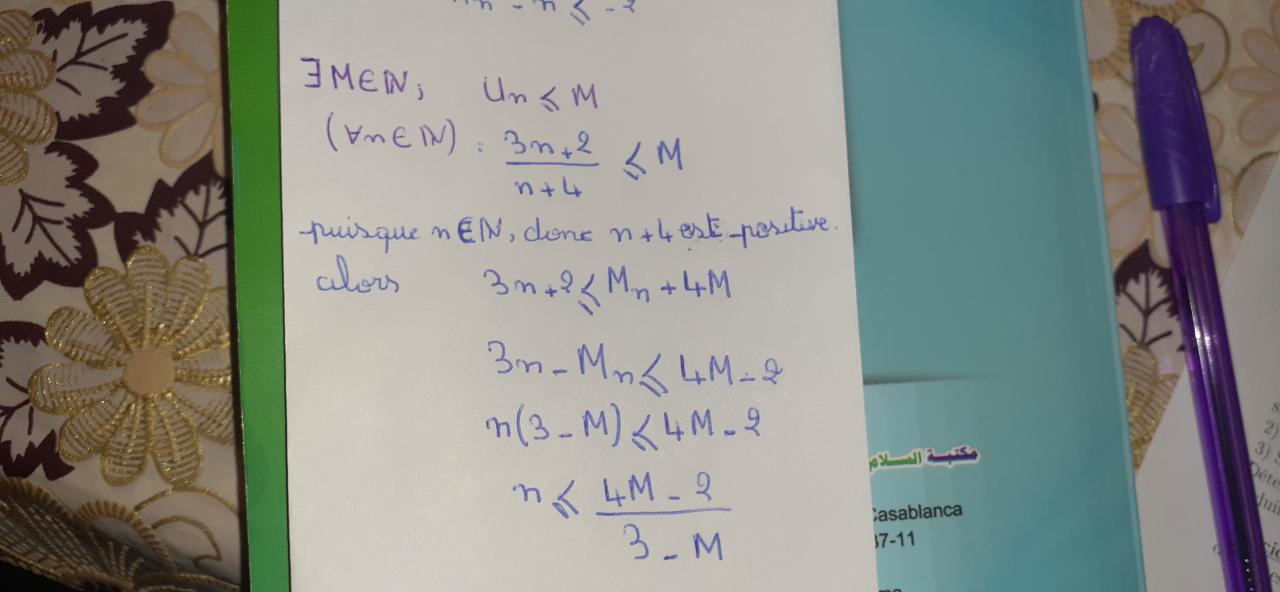3 questions à propos des suites numériques

[Mohamed amine nnn]

Salut tous le monde, j'ai besoin de l'aide ici.

D'abord l'énoncé de l'exercice est:
Soit une suite Un=n²-2n+3
la question demande de montrer que (Un) n'est pas majorée, alors on montrer ça avec le principe d'absurde comme la photo montre, du coup j'ai 3 questions:

1- Premièrement, je n'arrive pas à comprendre où est l'absurdité dans le résultat?

2- qu'est-ce la différence si on change l'ordre de (il existe) et (quelques soit) dans la réponse?

3- j'ai deja fait un exercice qui demande de montrer que Un<3 avec: Un=(3n+2)÷(n+4), et j'ai essayé de résoudre la question suivante: montrer que (Un) est majorée si on suppose que on ne sait pas que Un<3. J'ai essayé de la résoudre avec le principe de l'absurde mais je ne trouve pas la réponse ! (Sans utiliser les limites)

Merci.
-----

[albanxiii]

Bonjour et bienvenue sur le forum,

Je pense que vous avez mal posé les hypothèses de départ.
Dire que est majorée revient à dire qu'il existe tel que pour tout entier n on a .
Vous partez de cette hypothèse et vous montrez que vous arrivez à une contradiction.

Pourquoi la question 2 ?

[duduch74]

l'absurdité réside dans le fait que si Un est majorée par M, Un<M pour tout n entier naturel. Or toi tu montres que Un<M est vrai seulement pour certains entiers naturels n, ce qui est contradictoire avec la définition d'une suite majorée.

Pour la question 3, tu peux essayer de montrer qu'elle est convergente vers un réel et croissante. Et alors elle est majorée par ce réel. C'est un théorème de ton cours.

[gg0]

Bonjour Mohamed amine nnn.

Pour la question 2, si on change la phrase, ce n'est plus la même propriété.
La définition de "U_n est majorée" est "il existe un réel M tel que pour tout entier n, U_n<M"
Si tu écris "pour tout entier n, il existe un réel M tel que U_n<M", ça ne dit plus rien, puisque c'est vrai (par exemple on peut prendre M=n+1). Tu aurais pu le voir toi même en écrivant la phrase et en te demandant ce qu'elle dit.

Pour ta question 3, il est effectivement possible de démontrer "par l'absurde" (*) que U est majorée en supposant "U n'est pas majorée". Tu le traduis (il faut savoir nier une proposition), puis tu en déduis une contradiction. Mais c'est bien plus compliqué à faire que de justifier directement que ta suite est majorée par 3. Comme actuellement tu as déjà du mal à comprendre des preuves simples (ta question), il vaut mieux travailler les bases, puis revoir ça en supérieur(**), après des cours de logique.

Cordialement.

(*) En fait, ce n'est pas tout à fait la preuve par l'absurde, seulement la définition de "faux" : Soit P une propriété, si P implique quelque chose de faux, P est fausse.
(**) C'est le forum du collège/lycée, donc j'ai supposé que tu es en lycée.

[A voir en vidéo sur Futura]

[Mohamed amine nnn]

@duduch74 merci monsieur mais je n'ai pas étudié la suite convergente , je viendrai de l'étudier l'année prochaine in-chae-allah et merci énormément monsieur pour votre effort

[Mohamed amine nnn]

@gg0 Oui , j'ai essayé de le résoudre avec l'absurde mais je suis bloqué je ne sait pas comment je peux avancer !!
Du coup merci énormément monsieur pour votre temps c'est très gentille de votre part

[Mohamed amine nnn]

@albanxii D'accord monsieur merci énormément pour votre temps �� c'est très gentille de votre part

[Mohamed amine nnn]

Dans ma réponse j'ai supposé que Un est majorée et j'arrive au résultat dont la photo mais je ne sais pas comment l'interpréter pour prouver ma supposition . Merci énormément

[jacknicklaus]

Bonsoir

un indice :

d'autre part, donc ...

[gg0]

Bonjour Mohamed amine nnn.

Ton calcul est bon jusqu'à l'avant dernière ligne. La suite est incorrecte. Tu le comprendras facilement, puisque tu avais pris soin de vérifier le signe de n+4 au départ pour transformer l'inéquation. Comme tu n'as pas le signe de 3-M, tu ne peux pas passer à la dernière ligne.

Sinon, supposer que U est majorée ne sert à rien pour prouver qu'elle est majorée !! Ça pourrait servir si on voulait démontrer qu'elle ne l'est pas, mais comme elle l'est, tu perds ton temps. Tu as écrit une page pour rien (ça arrive souvent en maths, c'est aussi comme ça qu'on apprend).

Si tu veux démontrer qu'elle est majorée en supposant qu'elle ne l'est pas, il faut partir de "U n'est pas majorée".