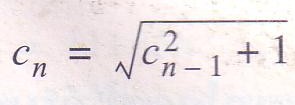est-ce une suite géométrique ??
Salut,
Voila j'ai un problème sur un exercice, je dois trouver si la suite suivante est géométrique ou pas, je ne sais pas de quelle manière je dois faire, est ce que c'est avec l'axiome de réccurence ou quelque chose d'autre. Cliquez sur le lien pour voir la suite.
Moi ce que j'ai fais j'ai calculé Cn+1 Mais est ce que cela suffit a démontrer que la suite n'est pas géométrique car je crois quel ne l'est pas mais j'attend votre aide pour me confirmer ca. merci
Si U1/U0 = U2/U1 alors elle est géo.
oui je veux bien mais avec la racine je fais comment ???
Exemple u0=1, u1=1, u2=1, u3=2, u4=5, ...Envoyé par M4tt
Ceci dit, l'approche proposée par m4tt, un peu modifiée par une application correcte de la logique du premier ordre, est une bonne piste...
Quand à la racine, un peu de manipulation algébrique permet de s'en occuper.
Cordialement,
pour la racine est ce qu'il faut utiliser l'expression conjuguée
Honnêtement, on n'a même pas besoin de se débarasser de la racine
Je suis d'avis de mmy, développe la piste proposée par M4tt mais modifiée (puisque l'assertion est fausse) : essaie d'écrire le rapport des premiers termes u2/u1, et u1/u0 puis compare-les . Si la suite est géométrique, alors nécessairement il faut que ces deux fractions soient égales, mais ça ne suffit pas (puisque pour que la suite soit géométrique, il faut que u(n+1)/u(n) soit une constante qui ne dépende pas de n). Par contre, si les deux fractions ne sont pas égales, alors tu es sûr que la suite n'est pas géométrique
