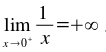La somme des entiers naturels existe ... et elle est négative

[prgasp77]

Bonjour à tous,
je me baladais sur Wikipédia, à la page de la fonction Zéta de Riemann, lorsque m'est apparut cette équation fonctionnelle :



Je me suis renseigné après coup, et celle-ci semble être approuvée sur différents sites (pourtant sérieux). Son soucis ? Elle implique que

Or, par définition,


J'ai alors continué mes recherches, et vu que Ramanujan avait remarqué ce paradoxe, mais apparemment, personne n'en a conclut que l'équation fonctionnelle était fausse en -1, voire sur tout le disque fermé ...
Quelqu'un peut-il m'éclairer là dessus ? Merci.
-----

[God's Breath]

La relation ne vaut que pour . Pour les autres valeurs de , la fonction est définie par prolongement analytique.

Il en est de même pour la fonction : la formule ne vaut que pour , les autres valeurs sont également définies par prolongement analytique

[prgasp77]

Oops ...
Et pourrais-tu m'en apprendre un peu plus sur ce prolongement, notamment sur son utilité. Merci beaucoup.

[God's Breath]

Dans un premier temps, voir prolongement analytique.

[A voir en vidéo sur Futura]

[breukin]

Une curiosité :
On a pour |z|<1 :

donc :

En appliquant brutalement à –1, on arrive à :

Or si on considère la fonction associée :

On a bien :

Comme si l'on devait affecter une valeur à une série divergente, il y avait une valeur particulière à privilégier , à laquelle on arrive par différents canaux ?

[breukin]

Je poursuis formellement :


Donc :


Mais les deux canaux ne sont peut-être pas si indépendants ?

[breukin]

Allez, encore un autre exemple :
On a pour |z|<1 :

donc :

En appliquant brutalement à 1, on arrive à :

Or si on considère la fonction

elle vérifie l'équation fonctionelle, analogue à celle de la fonction

On a bien !

[invite4ef352d8]

Salut !


cela peut paraitre en effet assez surprenant d'obtenir toujour la meme valeur, mais en fait, ca ne l'est pas tant que ca ^^


je vais prendre (parceque c'est le plus simple) l'exemple de la série somme des (-1)^k (k allant de 0 à l'infinie)



supposons qu'on est un moyen "raisonable" de la calculer (par exemple, regarder la valeur du prolongement de la somme des (-1)^k.x^k en x=1 ou la valeur du prolongement de (-1)^k/k^s quand s=0). et qu'on trouve une valeur S.

par raisonable, j'entend un procédé qui soit linéaire (si U et V sont deux série la somme de U+V c'est la somme de leurs sommes), et telle que si l'on enlève le premier de la série ou trouve la meme somme moins le premier terme.


du coup, si on applique ce meme moyen à la série "décaler" d'un cran : somme des (-1)^k k allant de 1 à l'infinie. on aimerait bien trouvé d'une part -S (parceque c'est la série opposé), et d'autre part S-1 (parceque on à enlever le premier terme)

du coup, on doit avoir S=1-S, et donc S=1/2

ainsi quelque soit le moyen 'raisonable' (et tous les moyens que tu propose sont raisonable) de calcule on trouvera forcement 1/2.

on peut appliquer le meme raisonement à toute les séries de la forme "somme des n", "sommes des n^2", "somme des a^n", "somme des n^17*b^n" etc... mais les raisonements formelle pour obtenir les valeur sont de plus en plus compliqué ^^

[mgarand]

J’ai lu la «*démonstration*» comme quoi la somme des entiers positifs serait un nombre négatif et de surcroît fractionnel (-1/12).
C’est une amusante supercherie, qui s’apparente à un tour de magie, réalisé grâce à une manipulation maline mais tout à fait abusive du langage mathématique.
Cette «*démonstration*» repose sur un mode d’écriture de l’opération *addition* qui est fautive, car cette écriture néglige le fait que l’infini n’est pas un nombre avec lequel on peut faire des opérations par exemple*: ∞-∞ =*? Ecrire ∞-∞ n’a pas plus de sens que d’écrire 1/0, qui a tout l’air d’être d’un nombre et qui n’en est pas un, c’est une écriture fautive comme il serait fautif d’écrire que ∞=1/0*: l’écriture mathématique convenable est que la limite de 1/x lorsque x tend vers 0 est l’infini ce qui en bonne écriture mathématique s’écrit*:



[B permettez que je vous démontre que 1=0

En utilisant la même manipulation fautive je vais vous démontrer que 0=1*; ce qui vous l'avouerais est encore plus fort*!
Soit S = 1+1+1+1+1+1+1 +…….
Calculons S-S selon la méthode des «*colonnes décalées*»
S-S = 1+1+1+1+1+1+...
-1-1-1-1-1-1- …
Toutes (*) les colonnes s’annulent, sauf la première et il reste donc 1
Donc S-S = 1
Or par définition même de la soustraction (qui est l’addition de l’inverse) S+(-S) qu’on écrit plus simplement S-S*: S-S=0
J’ai donc démontré que S-S = 1 Et S-S=0 donc 0=1.

Je pourrais d’ailleurs démontrer de la même manière que 2 = 0, et donc que 1= 2, et ainsi de suite montrer que tout les nombres entiers sont égaux, ce qui facilite ensuite tout les calculs et rend l’algèbre très simple, quoique bien sûr inutile*!

J’ai surtout démontré que ce mode opératoire (colonnes décalées) pour faire des additions quand la liste des nombres à additionner est infinie est fautive

D’ailleurs cette manière fautive de poser l’addition provient du fait qu’on ne peut pas écrire S=∞ et donc -S =-∞, alors pour échapper à cette écriture fautive on en invente une autre tout aussi fautive mais qui a l’air plus innocente*!

Pour conclure*: si la somme des entiers était un nombre fractionnel négatif voilà qui mettrait par terre la théorie des groupes de Galois, l’addition ne serait plus une loi interne à l’ensemble N et par là les fondements mêmes de l’algèbre s’effondreraient et tous les calculs algébriques deviendraient impossible, ce qu’on comprend bien dés lors que je pourrais démontrer que 0= 1. Si 0=1 , l’algèbre est morte*!

(*) Toutes*? c’est là que ce niche la faute … que veut dire ce «*toutes*» quand il s’agit d’une infinité*? Le propre de l’infini c’est de ne jamais être atteint et donc ne jamais avoir «*toutes*»

[Médiat]

Bonjour,

Cette "arnaque" a été dénoncée plusieurs fois ici, néanmoins votre "démonstration" n'est pas correcte, puisque vous utilisez une méthode que Riemann a démontrée fautive (Théorème de réarrangement de Riemann)

[mgarand]

Évidemment que ma démonstration est fautive ! c'est bien ce que je voulais démontrer d'ailleurs, ! Vous m'avez lu sans doute un peu vite !
je montre que la démonstration pour trouver -1/12 pour la somme des entiers est fautive, car en reprenant la même méthode j'arriverai à conclure que 0=1 =2 = 3 etc, que tous les nombres entiers seraient égaux, forcément il y a quelque chose qui cloche et j'en donne l'explication

[Médiat]

je montre que la démonstration pour trouver -1/12 pour la somme des entiers est fautive

Elle n'est pas fautive, mais ce n'est pas la somme au sens usuel, c'est pourquoi je parle d'arnaque

Je suis bien d'accord avec vous quand vous écrivez :

Cette «*démonstration*» repose sur un mode d’écriture de l’opération *addition* qui est fautive

mais pour moi la raison tient dans le fait que cette opération "infinie" n'est tout simplement pas définie, dans IN il n'est pas question d'écrire la moindre formule avec l'infini.

[mgarand]

Je ne veux pas chicaner, mais enfin faire une démonstration en utilisant un langage mathématique incorrect rend de facto la démonstration fautive, puisque que les mathématiques c'est d'abord un langage, et une démonstration consiste toujours, notamment quand il est question de s'appuyer sur des calculs, à écrire ligne après ligne la même chose différemment mais dans un langage qui doit rester correct, car le signe égal ne veut rien dire d'autre qu'exprimer la même chose de deux manières différentes dans le langage très formalisé des mathématique, il s'agit toujours de la même chose écrite de deux manière différentes de chaque coté du signe égal. Il convient donc que les deux manières soient toutes les deux écrites dans un langage mathématique correct, sinon c'est le signe égal lui-même qui n'a plus de sens !

Pour le reste nous sommes bien d'accord, et je considère que je démontre par l'absurde que pratiquer une "addition" par "colonne décalées" pour calculer la somme de "tous les entiers positifs" (expression qui n'a d'ailleurs aucun sens, puisque tous ne veut rien dire pour une infinité) et parvenir au fameux -1/12 est fautif, puisqu'en utilisant le même mode opératoire je peux démontrer que 0=1=2=3 etc, ce qui est absurde.
Je mets ainsi en évidence la coté fautif de ce mode opératoire dès que le nombre de colonne est ..infinie Ceci provient du fait que l'écriture de cette "addition" par colonnes décalées d'une infinité de nombres est une écriture mathématiquement fautive et elle conduit inéluctablement à un résultat faut.

[Médiat]

Tout ce que je voulais dire c'est qu'il existe une justification mathématique tout à fait légitime et rigoureuse, qui, à la suite définie par Un = n, associe -1/12 (mais ce n'est pas la somme).

[mgarand]

Là vous suscitez ma curiosité ! Et que serait donc cette valeur de -1/12 puisqu'en effet ce n'est pas la somme, l'impossible somme de tous les entiers ? Qu'est-ce donc ?

[Médiat]

Vous pouvez regarder :
http://forums.futura-sciences.com/ma...-a-1-12-a.html
http://forums.futura-sciences.com/ma...ml#post4516747
et même
http://forums.futura-sciences.com/ma...ml#post5659860

[pm42]

Là vous suscitez ma curiosité ! Et que serait donc cette valeur de -1/12 puisqu'en effet ce n'est pas la somme, l'impossible somme de tous les entiers ? Qu'est-ce donc ?

Lire les 4000 fils du forum qui en parle répondrait sans doute à votre question (comme déjà remarqué par Mediat plus haut). Une recherche sur "somme des entiers" permet de les trouver.

[gg0]

Mgarand :

On dirait que tu n'as pas lu les deux premiers messages, qui expliquent pourquoi on peut se permettre d'écrire par "extension" cette formule bizarre, sans que ce ne soit autre chose qu'une écriture limite qui ne parle pas de ce qui se passe quand on additionne les entiers indéfiniment (on sait que ça augmente indéfiniment). C'est un calcul purement formel (qui respecte la forme, que ça ait un sens ou pas).

Cordialement.

[mgarand]

"écriture par extension", "écriture limite" ; mais qu'est-ce que ça veut dire ? Les mathématiques ne supportent pas ce genre d'approximation du langage et d'objet non défini ! C'est tout simplement n'importe quoi !
Vous pouvez certes écrire n'importe quoi, c'est votre droit, même en usant et abusant de symboles mathématiques, si ça vous amuse ou si vous espérez épater les autres mais de là à prétendre à ce que ça soit intelligible c'est une autre affaire !
Tous ça n'est hélas pas sérieux !

On me propose de lire le fil de 4000 interventions dans ce forum pour y découvrir ce que pourrait signifier ce fameux -1/12 qui n'est pas la somme des entiers positifs mais qui auraient quand même quelque chose avoir avec, mais qu'il est mystérieusement impossible de nommer !
Je vous laisse à vos délires pseudo scientifiques si ça vous amuse de vous raconter des histoires à longueur de page .. !
Diafoirus est toujours vivant ! Il ne sévit pas qu'en médecine Monsieur Molière et au 21 ème siècle on en est pas moins prétentieux qu'au 17 ème quand il s'agit d'étaler un pseudo savoir en jargonnant ! Désolant ...
... donc désolé !

[mgarand]

Savez vous ce qu'est-une Quasi-somme ?
On appelle qS la quasi somme de tous des éléments d’un ensemble E dans lequel on a définit une opération*«*addition*»
On notera qS[E] la quasi-somme tous les éléments de l’ensemble E
Remarque*: Si P est un sous ensemble de E , comptant un nombre limité de k éléments qs[P] est égal à Somme S des k éléments, donc dans ce cas qS [P] = S*:
Premier Théorème : La quasi-somme est égale à la somme quand le nombre d’éléments à sommer est fini. Je ne vous inflige pas la démonstration que vous ferez sans doute facilement
Sinon, si le nombre d'éléments de E est infini ? Hé bien la quasi-somme est le plus souvent ce qu’on veut,
Par exemple on décide que la Quasi-somme des entiers positifs est égale à -1/12. ça fait plaisir à certains et ça mange pas de pain !
De toute façon ça n’a pas d’importance puisque ça ne sert à rien ! Pour l’instant ... me direz -vous, oui car allez savoir, dans ce forum quelqu’un va reprendre le concept de la quasi-somme et développer toute une branche magique des mathématiques à partir de ce concept.
Je consens qu’on associe mon nom à cette branche des mathématiques Merci d’avance*!

[Dynamix]

Vous connaissez la définition de la "somme pas usuelle" en math ?

Non , mais par exemple : 1+1=0
c' est pas franchement "usuel"
et il n' n'y a pas de raison pour se fâcher à cause de ça .

[Médiat]

On me propose de lire le fil de 4000 interventions dans ce forum pour y découvrir ce que pourrait signifier ce fameux -1/12 qui n'est pas la somme des entiers positifs mais qui auraient quand même quelque chose avoir avec, mais qu'il est mystérieusement impossible de nommer !

Désolant, mais pas désolé, car vous venez de vous ridiculiser, ce n'est par parce que vous ne comprenez pas la notion de prolongement analytique qu'ils sont des "délires pseudo-scientifiques".

[pm42]

On me propose de lire le fil de 4000 interventions dans ce forum pour y découvrir ce que pourrait signifier ce fameux -1/12

Non, on vous propose de vous renseigner avant d'affirmer n'importe quoi, ce qui est la base de la base.

Comme dit plus haut, votre discours est ridicule.

[Médiat]

Bonjour,

Je crois que tout a été dit : on ferme !

Médiat, pour la modération

[gg0]

Donc je ne réponds pas au message #19 !!!

[JPL]

Ça y est, j'ai sorti ma clé ! Celle de Médiat ne marchait pas.
Mission remplie.