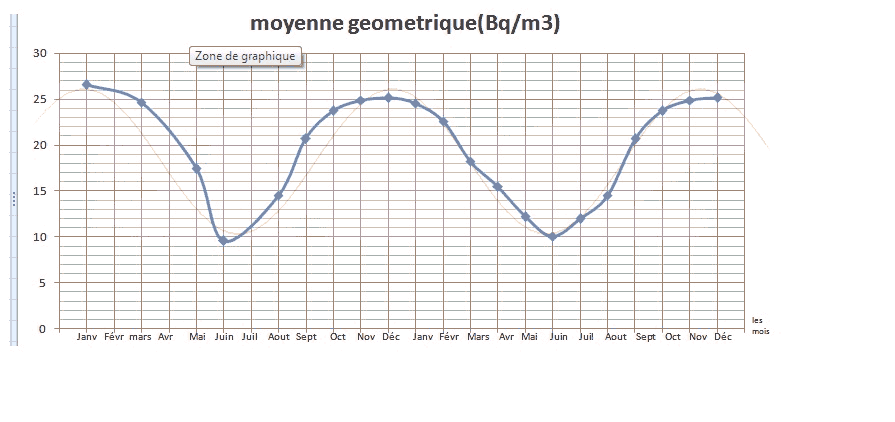
Bonsoir,
Pourriez m'expliquer comment trouver l'équation d'une fonction de la forme f(t)=a*cos(b*t+c), où a,b,c sont les inconnues, connaissant certaines valeurs de cette fonction pour différents instants t ?
J'ai pensé à la méthode des moindres carrés mais je ne vois pas comment l'utiliser pour cette fonction. J'ai essayé la fonction "minimize" de wolfram alpha mais je n'obtiens pas de valeurs pour a,b,c.
Merci d'avance
Ca n'a pas l'air trivial.
Peut être que ce document te serait utile ?
Par curiosité j'ai implémenté cette méthode et elle est complètement bluffante !Envoyé par HigginsVincent
salut, si tu au lieu de utilises comme modèleça sera plus simple et il suffira de chercher le maximum dans la densité spectrale de puissance (le module au carré de la transformée de Fourier de ta suite de points). Si tu as suffisament de points et que
@ acx01b
Tout dépend de la pertinence de la transformée de Fourier. Si l'on ne dispose que d'un petit nombre de points il est peu probable que le résultat soit significatif. De même si les points ne sont répartis que sur une fraction de sinusoïde. Pour savoir si la méthode est applicable, il faudrait que jimmypage77 donne plus d'information sur les donnés du problème (ordre de grandeur du nombre de points, indication sur leur répartition, ...)salut, si tu au lieu de utilises comme modèle ça sera plus simple et il suffira de chercher le maximum dans la densité spectrale de puissance (le module au carré de la transformée de Fourier de ta suite de points). Si tu as suffisament de points et que alors l'approximation sera négligeable.
@ jimmypage77
Pourrais-tu mettre sur le forum un exemple numérique de tes données. J'ai un programme disponible pour les traiter. Il serait alors possible de dire si la méthode décrite dans l'article suivant convient (ou non) à ton cas d'application.
"Régressions et équations intégrales", 3ième partie : "Régression sinusoïdale", procédure détaillé : pages 35-36 ( Pour l'application pratique de la méthode, il n'est pas indispensable d'avoir lu les explications données dans les pages précédentes qui sont un peu compliquées). L'article est accessible par le lien :
http://www.scribd.com/JJacquelin/documents
@ HigginsVincent
As-tu traité quelques exemples numériques ?Par curiosité j'ai implémenté cette méthode
Je serais intéressé par tes observations sur les résultats obtenus.
il s'agit de la transformée de Fourier des fonctions et ici des distributions, dont l'axe des fréquences est
Concernant la méthode proposée par acx01b :C'est bien comme cela que je l'ai compris, ce qui n'enlève rien à ma remarque (qui n'avait nulement l'intention de dénigrer cette méthode, mais seulement de signaler que, selon les données, le pic peut être trop peu marqué dans certains cas).il s'agit de la transformée de Fourier des fonctions et ici des distributions, dont l'axe des fréquences est R.
Voui, je peux les poster ici ou te les envoyer par MP, comme tu veux !
salut,
je ne suis pas sûr que ça soit bien clair pour toi. Le maximum du module de la TF est toujours la meilleure fréquence (en ayant pour modèle
@ HigginsVincentIl faut éviter de surcharger la discussion qui intéresse jimmypage77 par des exemples qui ne sont pas les siens. Si tu me transmets tes observations par message personnel, ce sera très bien et je t'en remercie par avance.je peux les poster ici ou te les envoyer par MP, comme tu veux !
@ acx01bL'utilisation d'une FFT pour répondre à ce genre de problème est une méthode qu'il m'est arrivé de proposer autrefois lorsque cette question était posée sur les forums de maths (on doit pouvoir retrouver des cas où j'ai répondu à la question par cette méthode basée sur TF). Donc, je ne suis pas contre, bien au contraire. Néanmoins, on peut dire tout ce qu'on veut, il n'y a que la comparaison des résultats concrets obtenus par application d'une méthode ou d'une autre pour voir laquelle est la plus fiable dans des conditions particulières. C'est pourquoi je demandais à jimmypage77 de mettre ses données numériques sur le forum.je ne suis pas sûr que ça soit bien clair pour toi. Le maximum du module de la TF est toujours la meilleure fréquence (en ayant pour modèle ) , par contre si le rapport de l'espace en les points est irrationnel, ce maximum peut être n'importe tout sur tout entier, ce qui rend donc la méthode assez peu intéressante au premier abord. Mais en approximant ce rapport par un rationnel assez proche, on peut majorer l'erreur (norme du résiduel) commise en restreignant l'étude de la TF sur un petit interval (dont la taille est égale au dénominateur du rationnel si je ne me trompe pas).
Bonjour,
Tout d'abord, merci pour les liens que vous m'avez fourni.
En fait, je m'intéresse à l'équation de cette sinusoïde afin de déterminer la masse de Jupiter. Je m'explique :
Modèle : J'ai considéré un modèle simplifié dans lequel les trajectoires elliptiques des satellites sont approximées par des trajectoires circulaires. Les satellites gravitant autour de Jupiter en suivant la 3ème loi de Kepler, il suffit de déterminer expérimentalement le rayon de la trajectoire circulaire et la période de chaque satellite pour obtenir 4 approximations de la masse de Jupiter.
Expérience : Lors de différentes soirées d'observation, j'ai enregistré les positions des satellites de Jupiter en plaçant une webcam au foyer de mon télescope. J'ai ainsi obtenu 9 clichés, répartis sur 6 jours consécutifs. Les pixels séparant le centre de Jupiter de chaque satellite sont en fait la projection, à différents instants, d'une trajectoire circulaire. J'ai donc mesuré la distance (en pixels) qui sépare le centre de chaque satellite du centre de Jupiter sur tous les clichés. J'ai alors essayé de faire une modélisation en sinusoïde afin de déterminer la période et le rayon de la trajectoire circulaire de chaque satellite.
Sur un logiciel comme Latis Pro, lorsque je rentre, avec mes données, un modèle du type r(t)=R*cos((2Pi/T)*t+Phi) (où R est le rayon de la trajectoire circulaire et T la période du satellite considéré), la modélisation ne "converge pas". C'est pourquoi j'essaye de déterminer l'équation de cette sinusoïde.
@JJacquelin
Voici les résultats obtenus pour le satellite nommé Europe :Pourrais-tu mettre sur le forum un exemple numérique de tes données. J'ai un programme disponible pour les traiter. Il serait alors possible de dire si la méthode décrite dans l'article suivant convient (ou non) à ton cas d'application.
Date Temps (h) Temps (s) Europe
16/01/2011 18h06 0 0 -119,4
17/01/2011 19h48 25h42 92520 97,3
17/01/2011 20h07 26h01 93660 99
17/01/2011 20h28 26h22 94920 100,7
18/01/2011 20h21 50h15 180900 72,1
18/01/2011 20h41 50h35 182100 68,1
19/01/2011 21h25 75h19 271140 -127,9
20/01/2011 18h53 95h51 345060 -34,2
21/01/2011 19h45 120h43 434580 134,1
Les signes + et - indiquent que le satellite se trouve respectivement à droite ou à gauche de Jupiter.
Les distances de la dernière colonne sont en pixels.
Toutefois, connaissant l'échantillonage (E=1.28") et le diamètre apparent de Jupiter au moment des observations, j'ai obtenu qu'un pixel représentait 3919 km.
Données théoriques :
- Période de Europe : 3j13h
- Distance à Jupiter : 671261 km
- Masse de Jupiter : 1.8986*10^27 kg
@JJacquelin
Pourrais-tu me dire si tu obtiens quelquechose avec ton programme ?
Merci d'avance.
En ayant seulement vu les données numériques (tracées sur la figure jointe), je savais d'avance que la régession échourait très probablement, ce qui s'est effectivement produit.
En effet, il n'y a que six points vraiment distincts (compte-tenu de ceux qui sont presque superposés). C'est très insuffisant. Il suffit de jetter un coup d'oeil à la figure 12 de l'article cité pour s'en rendre compte : Il n'a même pas été possible de tracer sur cette figure des cas avec un nombre de points inférieur à huit.
Donc, inutile de perdre ton temps à programmer cette méthode.
Je serais curieux de savoir ce que donne, pour cet exemple, la méthode proposée par acx01b. J'espère qu'il fera le calcul et nous indiquera ce qu'il obtient.
Ok, merci d'avoir essayé JJacquelin !
Sinon on m'a aussi conseillé d'utiliser les sommes de Riemann en initialisant une certaine valeur pour la période T.
Posons y(ti)=a*cos((2pi/T)*ti+c)
On a alors Sum(yi²*(ti+1 - ti))/T = 1/T*(intégrale de 0 à T de (a*cos((2pi/T)*t+c))²dt
En effectuant le changement de variable x=(2pi/T)*t+c, la somme est alors égale à pi*a².
Bonjour jimmypage77, j'ai peut-être une bonne nouvelle pour toi.
En effet, je n'avais pas fait attention à deux points importants dans l'énoncé de ton problème :
Premièrement, il n'y a que trois paramètres à optimiser alors que mon programme optimisait quatre paramètres.
Deuxièmement et c'est encore plus important, tu donnes une première approximation de w grâce à : Période de Europe = 3j13h
soit w voisin de 2*pi/(3600*(3*24+13))=0,00002533...
Le traitement devient très simple : une régression linéaire pour calculer deux paramètres (b et c de l'équation écrite sur la figure).
Attention, mes notations sont différentes des tiennes.
Ensuite, le calcul du coefficient ro et de l'angle phi est évident.
Déjà avec cette première approximation de w, le résultat est excellent et on peut se demander s'il y a lieu d'aller chercher mieux.
Toutefois, si l'on voulait ensuite moidifier un peu w pour réduire l'écart quadratique moyen (et ce ne pourra être qu'une très petite amélioration) , pratiquement toutes les méthodes itératives devraient donner de bons résultats, du fait de l'excellente valeur initiale connue pour w.
salut
voila le code matlab que j'ai fait :
il me trouve comme fréquenceCode:x = [0,92.52,93.66,94.9,180.9,182.1,271.14,345.06,434.58]*1000; octave:131> y = [-119.4,97.3,99,100.7,72.1,68.1,-127.9,-34.2,134.1]; octave:132> f = [0:1/max(x)/500:0.01]'; octave:133> TF = sum (bsxfun(@times,exp(2*i*pi*f*x),y),2); octave:134> [m,ind] = max(abs(TF)); octave:135> plot(x,y,'r+','MarkerSize',16) octave:136> hold on; octave:137> plot(2*real(TF(ind)*exp(-2*i*pi*[0:480]*f(ind)))/length(x)) octave:138> hold off;
et une image qui le montre
je pense qu'avec aussi peu de points il vaudrait mieux utiliser ma méthode comme initialisation de l'autre méthode proposée
Bonjour acx01b,
il y a sans doute une erreur dans tes conversions ou les unités choisies. En effet :ne correspond manifestement pas à ce qui est attendu pour une période voisine de 3j 13h soit T=306000 secondesil me trouve comme fréquence f=3.1617
La fréquence devrait être voisine de f=1/T=0,000003268
Il est probable que, pour tenir compte du facteur 1000 utilisé dans tes calculs, il aurait fallu diviser par 1000 au lieu de multiplier.
Ainsi ton résultat serait f=0,0000031617 , ce qui est bien l'ordre de grandeur attendu et en assez bon accord avec mon résultat f=w/2pi=0,0000032875
Ceci n'enlève rien a l'intérêt de ton calcul, en particulier dans un cas où l'on ne disposait que d'un aussi faible nombre de points expérimentaux.
Salut
j'ai le meme problème et je sait pas comment le résoudre!!!!!aidez moi SVP
plus des information sur mon problème ,j'ai fait des mesure pendant 2 année et donc je veux modéliser une une
phénomène par cette fonction:
f(t)= a*cos( b*t+c) mais je sait pas comment trouver a,b et c!!!
j'ai comme donné:
1ère année
t1 janvier ---->f(t1) connue
t2 janvier ---->f(t2) connue
.
.
.
t12 janvier ---->f(t12) connue
2ère année
t1 janvier ---->f(t1) connue
t2 janvier ---->f(t2) connue
.
.
.
t12 janvier ---->f(t12) connue
samrana,
As-tu des renseignements théoriques sur f ? (amplitude, période, etc.)
Bonjour,
Samrana, vous avez déjà ouvert un (deux en fait...) fil(s) sur ce sujet : http://forums.futura-sciences.com/ma...dre-une-e.html
Vous ne pourriez pas y rester ? Ca faciliterai la lecture et les réponses pour tout le monde.
@+
Not only is it not right, it's not even wrong!
j'ai seulement des valeur de f !!
Bonsoir,
Voir Cholesky.
JR
l'électronique c'est pas du vaudou!
re
précision cela fournit une approximation polynomiale.
JR
l'électronique c'est pas du vaudou!
mais j'ai un courbe comme ca
[ATTACH=CONFIG]2233
Pièce jointe 050[/ATTACH]
"Structurellement", votre fonction doit être périodique sur une année, non ?
Dernière modification par leon1789 ; 07/07/2013 à 22h02.
nn pas forcement par ce que a chaque mois a une valeur déférent a l'autre moi
Oui bien sûr, sur votre graphique, nous voyons bien des valeurs différentes pour le même mois de l'année. Mais cela ne signifie pas qu'il n'y a pas de périodicité sur un an pour le modèle théorique.
Mais bon, vous dîtes qu'il n'y a pas de périodicité d'une année, ok (...dommage, cela aurait donné la valeur de b précisément).
Cela étant, le cosinus de votre modèle a*cos( b*t+c) implique une périodicité : il serait bon d'en avoir une idée.
Dernière modification par leon1789 ; 08/07/2013 à 05h44.
Par ailleurs, j'ai l'impression que votre graphe est beaucoup trop rond entre septembre et mars pour que la cosinus de a*cos( b*t+c)+d soit un bon modèle...
Vous voulez un truc qui ressemblerait à ceci ?
Bonjour samrana,
Ton modèle f(t) = a*cos(b*t+c) ne convient pas du tout car cette fonction f(t) "oscille" de part et d’autre de 0. Au contraire, on voit que tes points expérimentaux sont tous supérieurs à 0.
Il faut faire intervenir un quatrième paramètre A :
f(t) = A + a*cos(b*t+c)
C’est donc une régression non-linéaire à quatre paramètres A, a, b, c
Je change les notations pour que ce soit en accord avec mes programmes de calcul et les notations de la figure ci-dessous (Le fait de remplacer ton cos par mon sin revient à changer la valeur de ta constante c). Nouvelle notation :
y(x) = a + R*sin(w*x+phi)
ce qui est la même chose que
y(x) = a + b*sin(w*x) + c*cos(w*x)
avec b= R*cos(phi) et c=R*sin(phi)
La méthode la plus simple consiste à fixer la valeur de la constante w :
w = 2*pi/12
(ce qui suppose que la fonction a exactement une période de 12 (en mois, c'est-à-dire de 1 an).
La régression porte alors sur les trois paramètres (a, b, c) de la fonction
y(x) = a + b*sin(2*pi*x/12) + c*cos(2*pi*x/12)
Elle est linéaire relativement à ces trois paramètres. C’est donc très simple à calculer (voir la méthode classique de régression linéaire par la méthode des moindres carrés, que l’on trouve dans tous les cours de statistiques). Le résultat est donné sur la figure jointe ( en bleu : valeurs des paramètres et courbe correspondante)
Si l’on ne veut pas imposer la valeur de w, la régression est non-linéaire, ce qui beaucoup plus compliqué. Il faut utiliser l’une des diverses méthodes qui sont décrites dans la littérature (faire une recherche sur la toile avec les mots clef "regression sinusoidale"). Il existe des logiciels de calcul où ces méthodes sont implémentées. Il suffit d’utiliser ces logiciels.
Toutes ces méthodes sont récursives (elles font des calculs successifs qui optimisent progressivement).
Une méthode non récursive est décrite dans l’article "Régression et équations intégrales" ( résumée pages 35, 36) :
http://www.scribd.com/JJacquelin/documents
Le résultat donné par cette méthode est présenté en rouge sur la figure.
On voit que w obtenu est un peu différent de 2pi/12 : On n’a plus exactement 12, ainsi qu’il fallait s’y attendre. Par contre, l’écart quadratique moyen (eqm) est un peu plus faible. Par conséquent, l’optimisation (au sens des moindres carrés) est améliorée, mais au prix d’une période qui ne respecte pas exactement le rythme annuel.
D’autres méthodes de régressions sinusoïdales donneraient des résultats légèrement différents pour w, donc pour la période, car elles seraient basées sur des critères d’optimisations qui ne sont pas toujours les mêmes.
Comme d’habitude, il faut savoir ce que l’on veut et donc choisir la méthode en fonction des critères que l’on considère comme essentiels.
