
- Forum
- Futura-Sciences : les forums de la science
- MATHEMATIQUES
- Mathématiques du supérieur
- Théorème des quatre couleurs
Théorème des quatre couleurs
- 25/06/2016, 10h14 #91invitebd98b571

- Date d'inscription
- janvier 1970
- Messages
- 191
Re : Théorème des quatre couleurs
------

- 25/06/2016, 11h15 #92Médiat
- Date d'inscription
- août 2006
- Âge
- 75
- Messages
- 20 622
Re : Théorème des quatre couleurs
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
- 25/06/2016, 12h45 #93invite75a796c1

- Date d'inscription
- janvier 1970
- Messages
- 738
Re : Théorème des quatre couleurs
C'est quand même dommage de ne pas être dans le forum Enigmes, du coup on ne peut pas exiger de jeu d'essai ...
Et si nous nous mettions d'accord sur un format ?
Ensuite le challenge* serait de faire mieux que celui qui a mieux fait : nous pourrions ainsi tenir tout l'été !
Sinon, tant pis ...
* Ce ne serait pas vraiment un challenge entre nous mais plutôt un jeu collectif.
- 25/06/2016, 13h05 #94Dlzlogic
- Date d'inscription
- juillet 2011
- Messages
- 2 117
Re : Théorème des quatre couleurs
Bonjour,
A propos d'enclave, il y a deux solutions, soit une enclave de deux communes à l'intérieur d'un département (mon exemple de 2 communes du PdC isolées dans le Nord), soit une région (resp. pays) à l'intérieur d'un pays.
Dans le premier cas, les deux communes devront avoir la couleur de leur département, dans le second cas, (de mémoire) je l'ai traité. C'est en fait le cas général d'une zone qui n'a qu'un voisin. On le trouve dans le cas de la Corse (Nord et Sud).
@ Mike, ce serait assez amusant de faire des essais, voire un concours. J'ai un tas de fichiers qui correspondent aux hypothèses, y'à qu'à choisir. Mais, je tiens à vous prévenir, le traitement des zones en général n'ai pas très facile, et c'est le "pré-traitement" obligatoire. Petit exemple simple, on a 3 zones limitrophes A, B, C. On a réussi à tester que A et B ont une limite commune, ainsi que A et C et B et C. Soit on sait comment elles sont organisées (méthodes ds triangles) soit on le ne sait pas (méthode de graphe), alors, ça me parait couteux à traiter.
- 25/06/2016, 13h54 #95invite9dc7b526
- Date d'inscription
- janvier 1970
- Messages
- 6 218
Re : Théorème des quatre couleurs
Allez je continue avec mes considérations générales:
pour 4 couleurs, si on raisonne en termes de graphes, le théorème des quatre couleurs donne une condition suffisante (planaire => 4-colorable) mais on peut voir que cette condition n'est pas nécessaire puisque le graphe "des 3 maisons et des 3 puits", K3,3, qui est bien connu pour ne pas être planaire, est évidemment colorable avec 2 couleurs.
- 25/06/2016, 18h16 #96invite75a796c1

- Date d'inscription
- janvier 1970
- Messages
- 738
Re : Théorème des quatre couleurs
pas grave ; il faut au moins un gros jeu d'essai dans un format commun aux joueurs@ Mike, ce serait assez amusant de faire des essais, voire un concours. J'ai un tas de fichiers qui correspondent aux hypothèses, y'à qu'à choisir. Mais, je tiens à vous prévenir, le traitement des zones en général n'ai pas très facile, et c'est le "pré-traitement" obligatoire. Petit exemple simple, on a 3 zones limitrophes A, B, C. On a réussi à tester que A et B ont une limite commune, ainsi que A et C et B et C. Soit on sait comment elles sont organisées (méthodes ds triangles) soit on le ne sait pas (méthode de graphe), alors, ça me parait couteux à traiter.
- 25/06/2016, 19h15 #97Dlzlogic
- Date d'inscription
- juillet 2011
- Messages
- 2 117
Re : Théorème des quatre couleurs
Je pense à deux fichiers, les départements Français et les régions Européennes. Je pense les avoir tous les deux en format SHP et MIF/MID. Ce sont des formats très connus, mais bon courage si vous partez de rien.
Je me pose une question. Est-ce le problème des quatre couleurs qui a donné l'idée des graphes, ou au contraire, la théorie des graphes existe et on l'a appliquée au problème des quatre couleurs ?
- 25/06/2016, 22h57 #98invite23cdddab
- Date d'inscription
- janvier 1970
- Messages
- 2 151
Re : Théorème des quatre couleurs
Pas très intéressant comme jeu d'essai... ça va surtout tester la vitesse du prétraitement et pas celle de l'algorithme de coloriage en lui même.

- 26/06/2016, 05h29 #99Seirios
- Date d'inscription
- mai 2005
- Localisation
- Dans le plan complexe
- Âge
- 34
- Messages
- 10 382
Re : Théorème des quatre couleurs
Si l'on en croit wikipédia, la théorie des graphes a été introduite avant que le problème des quatre couleurs se pose. Ce n'est pas étonnant en soit, le problème de coloration est tout de même assez restreint.If your method does not solve the problem, change the problem.
- 26/06/2016, 11h32 #100invite75a796c1

- Date d'inscription
- janvier 1970
- Messages
- 738
Re : Théorème des quatre couleurs
Etonné de ne pas trouver de résolution avec des méthodes syntaxiques, je sentais le présumé challenge intéressant.Je pense à deux fichiers, les départements Français et les régions Européennes. Je pense les avoir tous les deux en format SHP et MIF/MID. Ce sont des formats très connus, mais bon courage si vous partez de rien.
Je me pose une question. Est-ce le problème des quatre couleurs qui a donné l'idée des graphes, ou au contraire, la théorie des graphes existe et on l'a appliquée au problème des quatre couleurs ?
Disposant de temps cette semaine, j'aurais surement proposé un couple syntaxe-IA pour retrouver une partie des 500 cas de base. Mais ça a trainé , le temps a passé ...
la piste : il faut utiliser yaml ou un de ses clones. Une analyse d'expressions et un résolveur en force brute des sous-graphes théoriques ( à utiliser une seule fois par sous-graphe ) devrait suffire à faire un petit programme léger et rapide. Il faudra surement tâtonner avant de déterminer la liste des sous-graphes efficaces. Une bonne semaine quoi ...
- 26/06/2016, 12h20 #101Dlzlogic
- Date d'inscription
- juillet 2011
- Messages
- 2 117
Re : Théorème des quatre couleurs
Bonjour,
Si cela semble intéressant, pas d'objection pour écrire un fichier dans un format simple qu'on voudra bien me préciser, et qui rendra minimal ce que certains appellent le prétraitement.
Bonne journée.
- 26/06/2016, 12h32 #102invite9dc7b526
- Date d'inscription
- janvier 1970
- Messages
- 6 218
Re : Théorème des quatre couleurs
la recherche d'un ensemble de "configurations inévitables" est la partie difficile du programme d'Appel & Haken. Il faut voir que cet ensemble n'est pas unique. Dans l'article initial, le nombre de configurations était d'environ 2000, maintenant on est descendu à moins de 500. L'algorithme d'Appel & Haken fait appel a une heuristique probabiliste, c'est à mon humble avis le point crucial dans leur démarche (et peut-être celui qui a été le plus critiqué).
mouais...Une bonne semaine quoi...
- 26/06/2016, 17h19 #103invite75a796c1

- Date d'inscription
- janvier 1970
- Messages
- 738
Re : Théorème des quatre couleurs
ben mon ami, fournissez un jeu d'essai ... je n'ai pas la semaine d'une traite mais on verra bien.
A mon avis, la difficulté n'est pas de trouver un moyen de décoder les cas d'un jeu d'essai, mais de démontrer la pertinence et l'existence d'un ensemble de sous-graphes , montrer qu'il est unique ou non et d'en exhiber un dont tous les éléments ont été résolus.
Ca, je n'y prétends pas. M'appuyant sur ce résultat, je me propose de rechercher de manière hiérarchisée des régularités en nombre fini ( en utilisant le générateur Yaml ) comme le fait un compilateur quand il analyse une expression. Sauf que la syntaxe sera apprise au fur et à mesure des "syntax errors" rencontrées. Une suite d'instructions est aussi un long graphe.
Il serait motivant de disposer au préalable de tous les sous-graphes et d'utiliser le même type de fichiers que les auteurs.
- 27/06/2016, 08h54 #104invite9dc7b526
- Date d'inscription
- janvier 1970
- Messages
- 6 218
Re : Théorème des quatre couleurs
ah donc tu parles d'un algorithme de coloriage. Comme tu faisais allusion aux 500 cas je pensais que tu voulais reproduire la démonstration du théorème des quatre couleurs.
Pour un algorithme de coloriage est-ce pertinent de chercher dans le graphe à colorier l'une des configurations qui apparaissent dans la preuve? Il faut savoir que dans la preuve du théorème on se limite aux triangulations. L'une des 500 configurations en questions apparaît nécessairement dans une triangulation, mais pas dans un graphe planaire quelconque. Donc il te faudrait commencer par ajouter des arêtes à ton graphe de façon à en faire une triangulation. Puis repérer la configuration dans la liste des 500 possibles. Ensuite, quoi?
- 27/06/2016, 12h33 #105Dlzlogic
- Date d'inscription
- juillet 2011
- Messages
- 2 117
Re : Théorème des quatre couleurs
Bonjour,
"ben mon ami, fournissez un jeu d'essai ... je n'ai pas la semaine d'une traite mais on verra bien. "
J'ai répondu hier soir, et soit j'ai fait une fausse manipe, soit ma réponse est en attente de validation. Dans le doute, je recommence
http://www.dlzlogic.com/France_Dep/dep_france_dom.shp
http://www.dlzlogic.com/France_Dep/dep_france_dom.shx
- 27/06/2016, 12h37 #106invite75a796c1

- Date d'inscription
- janvier 1970
- Messages
- 738
Re : Théorème des quatre couleurs
ensuite colorier le sous graphe avec une résolution brute effectuée une seule fois par sous-graphe et pouvant être inscrite en dur dans les paramètres du programme.
Enfin, effectuer l'ajustement des palettes hiérarchiquement au fil de la lecture, avec parfois plusieurs sous-solutions.
Le graphe d'origine peut toujours être linéarisé, ce n'est qu'un artifice pour une acquisition séquentielle.
- 27/06/2016, 12h44 #107invite9dc7b526
- Date d'inscription
- janvier 1970
- Messages
- 6 218
Re : Théorème des quatre couleurs
Mais rien ne dit a priori que le coloriage d'un certain sous-graphe puisse être étendu au graphe entier.

- 27/06/2016, 12h51 #108invite75a796c1

- Date d'inscription
- janvier 1970
- Messages
- 738
Re : Théorème des quatre couleurs
Prenons un sous-graphe résolu. Les 4 couleurs trouvées aux frontières ne sont que des indices dans une palette. Quand on réunit plusieurs sous graphes, des solutions partielles deviennent incompatibles mais il en reste forcément au moins une. C'est un corrolaire de l'existence d'une démo valide. Il y a au maximum 24 solutions de palettes aux frontières de chaque sous-graphe, indépendamment de sa taille.
ps : message écrit avant de vous avoir lu mais ça tombe bien
- 27/06/2016, 13h27 #109invite9dc7b526
- Date d'inscription
- janvier 1970
- Messages
- 6 218
Re : Théorème des quatre couleurs
Ca ne me paraît pas évident. Qu'il existe un coloriage du sous-graphe qui puisse être étendu au graphe entier, c'est clair d'après le théorème des quatre couleurs, mais que tout coloriage puisse l'être ne me semble pas vrai (j'ai la flemme de chercher un contre-exemple mais ça ne doit pas être dur). Donc si tu colories un sous-graphe sans tenir compte de ce qu'il y a autour, rien ne te garantit que tu ne devras pas revenir sur ce coloriage.

- 27/06/2016, 14h27 #110invite75a796c1

- Date d'inscription
- janvier 1970
- Messages
- 738
Re : Théorème des quatre couleurs
oui, ajuster les palettes c'est un peu "revenir en arrière" mais ce n'est pas tout reprendre à zéro.
Un sous-graphe donné, éventuellement lui-même composé de sous-graphes, est pour le reste du graphe une suite fermée de segments colorés. Son intérieur est opaque. Je suis confiant dans la réduction hiérarchisée des inconnues et la capacité d'un tel programme de trouver une expression de toutes les solutions de coloriage possibles. C'est la force de l'existence du théorême. Sans lui, minimiser des voies élémentaires qui ont forcément des solutions ne serait plus une stratégie sure.
- 27/06/2016, 16h18 #111invite75a796c1

- Date d'inscription
- janvier 1970
- Messages
- 738
Re : Théorème des quatre couleurs
Bonjour,Bonjour,
"ben mon ami, fournissez un jeu d'essai ... je n'ai pas la semaine d'une traite mais on verra bien. "
J'ai répondu hier soir, et soit j'ai fait une fausse manipe, soit ma réponse est en attente de validation. Dans le doute, je recommence
http://www.dlzlogic.com/France_Dep/dep_france_dom.shp
http://www.dlzlogic.com/France_Dep/dep_france_dom.shx
super , c'est un début.
Il va d'abord falloir comprendre comment ce format fonctionne pour obtenir une représentation par éléments au sens du pb.
J'ai trouvé de la doc.
Merci.
- 28/06/2016, 11h48 #112invitebd98b571

- Date d'inscription
- janvier 1970
- Messages
- 191
Re : Théorème des quatre couleurs
Bonjour
C'est vraiment dommage que les formats des fichiers soient "quasi-cryptés". Avec quels logiciels spécialisés peut-on les lire ?
Dlzlogic, pouvez-vous donner un fichier texte que tout le monde peut lire facilement ?
- 28/06/2016, 12h43 #113Dlzlogic
- Date d'inscription
- juillet 2011
- Messages
- 2 117
Re : Théorème des quatre couleurs
Bonjour,
Il est vrai que ce n'est simple de lire des fichiers du type géographique.
Si je le met sous forme :
X0 ; Y0
X1 ; Y1
.....
X0 ; Y0
Pour chaque département, cela vous convient ?
Sinon, indiquez-moi un autre format.
- 28/06/2016, 13h26 #114invitebd98b571

- Date d'inscription
- janvier 1970
- Messages
- 191
Re : Théorème des quatre couleurs
Si possible, je serais ravi d'un fichier texte écrit sous la forme d'ensemble de coordonnées des points de la zone
zone 1 = { [x0, y0], [x1, y1], ....... }
zone 2 = { [x0, y0], [x1, y1], ....... }
.etc.
- 28/06/2016, 15h12 #115Dlzlogic
- Date d'inscription
- juillet 2011
- Messages
- 2 117
Re : Théorème des quatre couleurs
Bonjour,
J'ai créé un fichier suivant votre format;
http://www.dlzlogic.com/France_Dep/France_Dep2016.TXT
Je n'ai pu faire qu'un contrôle visuel.
Il est certain que c'est une version un peu simplifiée, Il est probable que des enclaves et trous soient purement et simplement ignorés. Très possible que les N° de zone ne correspondent pas aux N° de département.
Par ailleurs, ça m'a bien amusé de remettre le nez dans ce programme.
Bon calcul.
- 28/06/2016, 18h51 #116invitebd98b571

- Date d'inscription
- janvier 1970
- Messages
- 191
Re : Théorème des quatre couleurs
Merci beaucoup d'avoir fait l'effort de déposer un tel fichier
Facile de colorier Voici la carte :
Voici la carte :
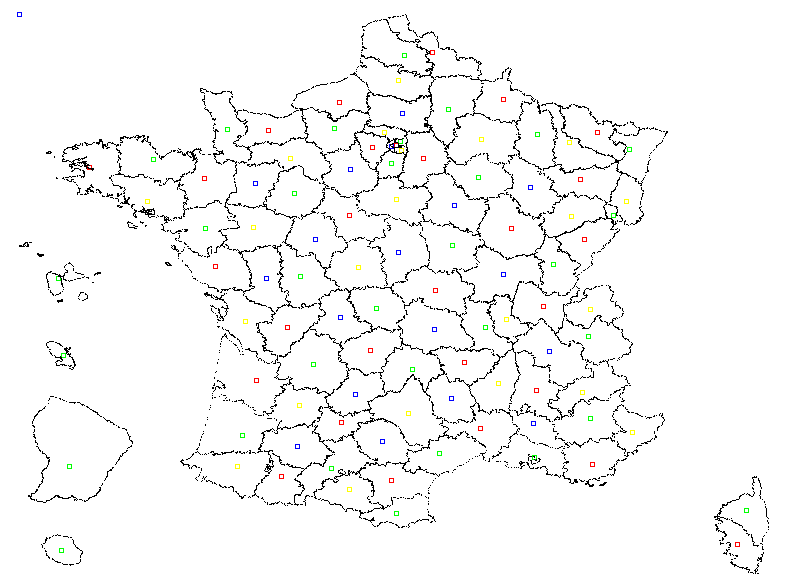
Vous remarquez le carré bleu en haut à gauche de l'image qui indique que la zone extérieure est coloriée en bleu. Ce qui implique que tous les départements au bord doivent être de couleur différente.
Et votre solution ?
- 28/06/2016, 19h10 #117Dlzlogic
- Date d'inscription
- juillet 2011
- Messages
- 2 117
Re : Théorème des quatre couleurs
Oui, ça a l'air impeccable.
Ce n'est pas tellement le résultat qui m'a fait ouvrir ce sujet, mais la méthode basée sur les triangles qui me paraissait intéressante.
Je suppose que vous avez attaché à chaque département le numéro de ses voisins, puis cherché une attribution de couleur en utilisant un graphe.
Vous utilisez quel langage ou quel logiciel ?
- 28/06/2016, 20h52 #118invitebd98b571

- Date d'inscription
- janvier 1970
- Messages
- 191
Re : Théorème des quatre couleurs
Merci

D'accord. Mais j'aurais aimé savoir ce que donne votre méthode à base de triangles lorsqu'on a ajoute la grande zone englobante, s'il vous plait.
Oui, la première étape est bien la détection des zones qui sont voisines (zones => graphe) par calcul d'intersection des frontières.
La seconde est effectivement le coloriage du graphe résultant (le grande zone englobante augmente un peu la difficulté).
Et la troisième est de coller les couleurs sur les zones (graphe => zones).
un logiciel de calcul formel (pour uniquement la gestion aisée des ensembles), mais tout langage de programmation peut convenir en gérant soi-même des tableaux.
- 29/06/2016, 01h43 #119invite75a796c1

- Date d'inscription
- janvier 1970
- Messages
- 738
Re : Théorème des quatre couleurs
Salut,
joli travail
Avez vous essayé votre algo avec des configurations plus compliquées ?
J'irai beaucoup moins vite ...
- 29/06/2016, 09h45 #120invitebd98b571

- Date d'inscription
- janvier 1970
- Messages
- 191
Re : Théorème des quatre couleurs
Bonjour
non, je n'ai pas essayé avec des configurations plus compliquées.
Juste pour les yeux, le cheminement de l'algo heuristique à son 39ème et dernier essai :
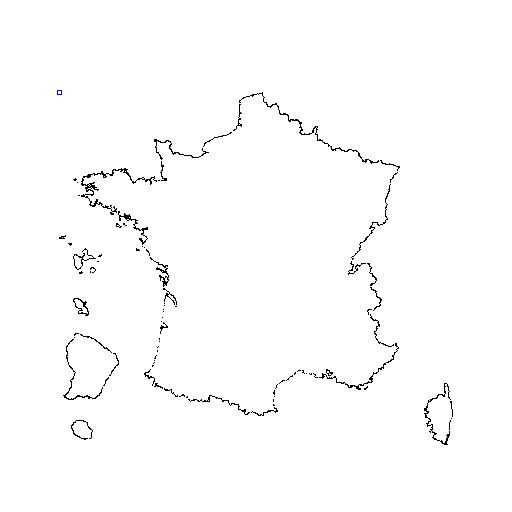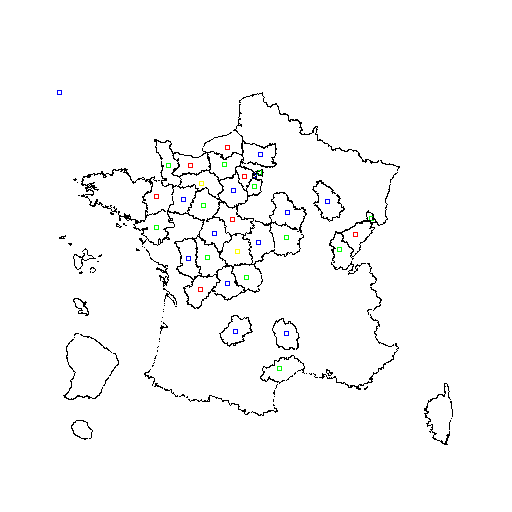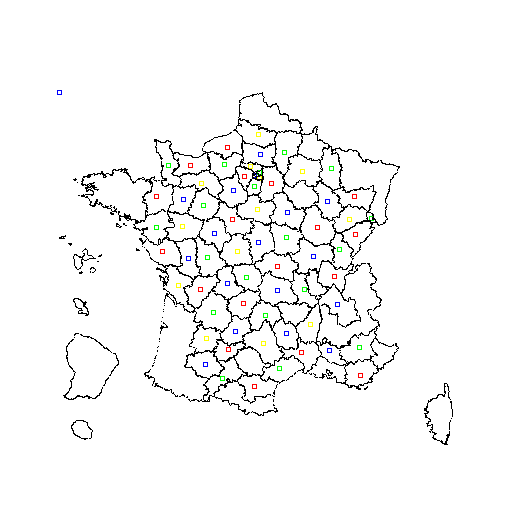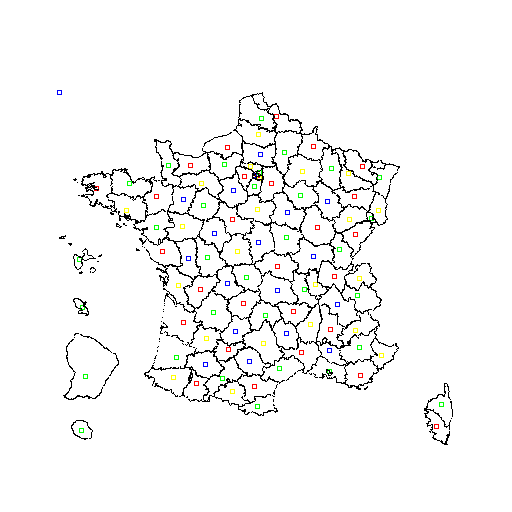

Discussions similaires
-
Tous les spectres de couleurs, couleurs RGB, et couleurs monochromatiques
Par acx01b dans le forum PhysiqueRéponses: 31Dernier message: 03/08/2014, 20h57 -
théorème des 4 couleurs
Par inviteeb9ddbba dans le forum Mathématiques du supérieurRéponses: 66Dernier message: 31/03/2009, 17h51 -
Théorème des Quatre Carrés
Par invited3e24d42 dans le forum Mathématiques du supérieurRéponses: 4Dernier message: 22/06/2008, 11h29 -
Théorème des quatres couleurs - revues scientifiques
Par invite3e257a4d dans le forum Mathématiques du supérieurRéponses: 0Dernier message: 07/11/2007, 17h33 -
Quatre couleurs
Par invite693d963c dans le forum Mathématiques du supérieurRéponses: 4Dernier message: 06/12/2005, 22h08
Fuseau horaire GMT +1. Il est actuellement 16h49.

