Relation suite des predecesseurs impaires des premiers et position des carrés

[invite84127968]

Il semble que ma pièce jointe n°2 dans mon message précédent ne soit pas valide: je la remet donc:


-----

[invite84127968]

Pas trop de temps ce matin, mais en faisant un petit test rapide en me levant:

(n*4)-3 puis -2, même principe qu'avant... cette fois tout les carrés sont dans les mêmes colonnes et la colonne 81 comporte tout les carrés successifs au moins jusqu'à 4761.

[Merlin95]

Si tu réponds pas aux messages qui te sont posés cest un monologue et cest assez irrespectueux.

[ansset]

@Lyet:

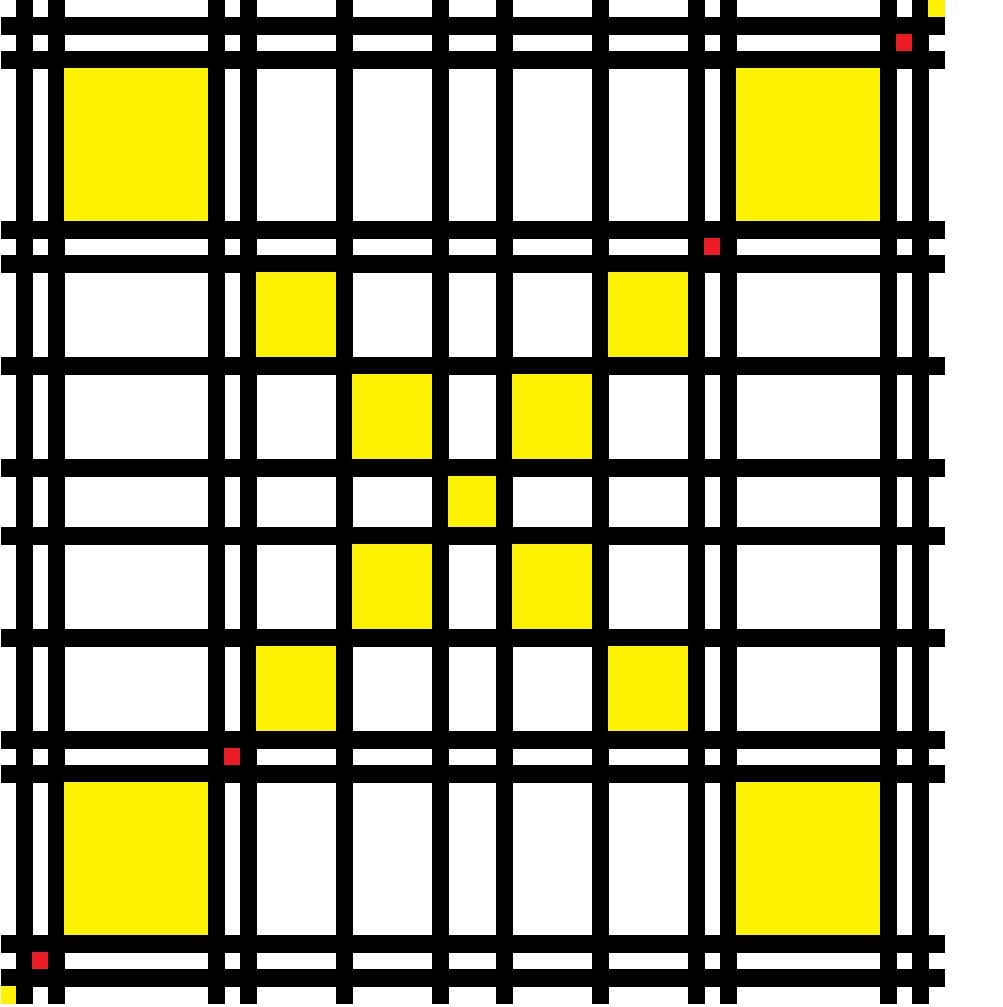
Ce que Je cherche est une structure isomorphe dans les écarts entre nombre premier qui puisse m'amener à développer graphiquement cela :

soit la figure ( à la Mondrian ) du post 31 ?
qui serait une figure recherchée et non obtenue je suppose ?

si c'était si simple ?????

[invite84127968]

Si tu réponds pas aux messages qui te sont posés cest un monologue et cest assez irrespectueux.

En même temps l'heure de mon dernier post est celle juste avant que je parte bosser et celle de celui ci juste après que je rentre: je tenterai de reformuler plus proprement dès que j'ai un peu de temps..

[invite84127968]

@Lyet:

soit la figure ( à la Mondrian ) du post 31 ?
qui serait une figure recherchée et non obtenue je suppose ?

si c'était si simple ?????

La figure à la Modrian existe, elle se révèle en colorant les colonnes et les lignes sur tableur en plaçant les entiers naturels en abscisse et ordonné, les lignes noirs sont les nombres premiers: pour celle en post 31, il s'agit d'un intervalle entre deux nombres premiers dans lequel les écarts sont isomorphes (j'utilise peut-être ce terme de façon galvaudée, symétrique serait plus juste?).
L'idée est de chercher ou ce genre de figure peut se retrouver dans ces écarts, l'important étant de garder la proportion: sont -elles uniques ou pas? C'est un peu ce que cherche.

Pour la formule de ce matin j'analyse, ceux qui ont suivis peuvent peut-être déjà avoir vérifier si on retrouve le même résultat qu'avec n=19 (pour mémoire somme des prédécesseurs impaires de 19=100 d’où le côté intéressant )

[invite84127968]

Pour la formule de ce matin la succession des carrés obtenus s’arrête à 79^2
La suite obtenue avec ces écarts est la suivante:

81.jpg

Observations rapides: 81 n'est pas un premier, 4 premiers carrés successifs correspondent à 4 premiers n successifs..

[invite84127968]

Observations rapides: et somme des écarts ne peut être impaire donc = à 81 car les écarts entre premiers sont paires pour n>2.
Il y a moyen de trouver une formule généralisatrice de cette relation.. pas le temps ce matin.

[ansset]

La figure à la Modrian existe, elle se révèle en colorant les colonnes et les lignes sur tableur en plaçant les entiers naturels en abscisse et ordonné, les lignes noirs sont les nombres premiers: pour celle en post 31, il s'agit d'un intervalle entre deux nombres premiers dans lequel les écarts sont isomorphes (j'utilise peut-être ce terme de façon galvaudée, symétrique serait plus juste?).
L'idée est de chercher ou ce genre de figure peut se retrouver dans ces écarts, l'important étant de garder la proportion: sont -elles uniques ou pas? C'est un peu ce que cherche.

je ne comprend pas toujours pas vraiment ( notamment le lien entre ton graphique et tes "résultats" ), et pourtant force est de constater que tu cherches à expliquer tes démarches.
je préfère donc laisser ceux qui ont compris faire leurs commentaires éventuellement.
cordialement.

[Merlin95]

En même temps l'heure de mon dernier post est celle juste avant que je parte bosser et celle de celui ci juste après que je rentre: je tenterai de reformuler plus proprement dès que j'ai un peu de temps..

En même temps cest pour toi et pouvoir te dire si ce sur tu fais est intéressant que je dis ça. Si tu veux continuer à faire mumuse dans ton coin je vois pas trop l'intérêt de venir en parler ici. Mais c'est toi qui voit. Je préfère aussi laisser intervenir ceux qui ont compris ta démarche.

[invite84127968]

je ne comprend pas toujours pas vraiment ( notamment le lien entre ton graphique et tes "résultats" ), et pourtant force est de constater que tu cherches à expliquer tes démarches.
je préfère donc laisser ceux qui ont compris faire leurs commentaires éventuellement.
cordialement.

Je suis en mesure de montrer l'idée concernant ce lien, la première formule donnée génère un écart de 2 entre les colonnes contenant des carrés, la seconde génère des écarts de 2,4 et 6 avec une succession unique de deux 6 pour les colonnes 73 et 79: les écarts entre carrés de même valeur, d'une ligne à l'autre sont ce que je regarde en ce moment.

Evolution des écarts entre colonnes contenant des carrés pour la formule (n*4)-3, puis -2:




Je vais avoir un peu plus de temps ce soir pour m'expliquer plus précisément...

[invite84127968]

Je reprends le fil, j'ai remis la main sur le lien entre la figure "Modrian" et les carrés selon la formulation (n*x)-k*(x-1) pour n étant premier (@Merlin95 c'est ainsi que l'on peut créer les suites dont je parle).

"Figure de Modrian", il s'agit des écarts entre premiers dans l'intervalle des premiers successifs de 137 à 193. Cette suite comporte 11 nombre, elle est isomorphe, je l'avais remarqué en étudiant les partitions du nombre 11.
La suite : (2,10,2,6,6,4,6,6,2,10,2), sa somme est de 56, le nombre de partitions du nombre 11 est aussi 56. En faisant la somme des termes de cette suite de cette façon terme1+(terme1+terme2)+(t1+t2+ t3)+..(t1+t2+t3+t4+t5+t6+t7+t8 +t9+t10+t11)...+(t8+t9+t10)+(t 9+t10)+t11 on obtiens 616 soit la somme des partitions du nombre 11 (11*56):

Pièce jointe 397245

Remarquable, (à lire éventuellement après le reste) : la somme des premiers de 137 à 193 est de 1980 (2^2*3^2*5*11) 36 diviseurs (2^2*3^2), la même opération de somation que pour obtenir 616 avec les écarts donne une suite:
(137,276,425,576,733,896,1063, 1236,1415,1596,1787,1980,1980, 1704,1555,1404,1247,1084,917,7 44,565,384,193) les sommes intermédiaires ( de 137 à 193, de 276 à 384, de 425 à 565,..et de 1787 à 1980) donnent une suite linéaire:

Pièce jointe 397247

De ces constatations j'en reviens à l'objet principal du message, le lien entre cette suite d'écarts et les positions des carrés dans les suites décrites en préambule.
J"ai pris en formulation (n*11)-10 pour vérifier si il y avait une construction particulière. Le tableau est le suivant:



Les carrés 121 ont les positions suivantes: 7,29,40,62,95,106... avec dons des écarts entre elles 29-1=22 (2*11), 40-29=11,62-40=22,95-62=33 écarts multiples de 11.
A remarquer donc que les colonnes pour ces positions sont des multiples de 11.
Dans l'intervalle "Modrian" de 137 à 193 les suites des (n*11)-k*(11-1) a pour somme des écarts 616.

Voilà pour les détails, merci de votre patience.

[invite84127968]

Correctif dans la formule lire (n*x)-(x-1)-k*2 et non (n*x)-k*(x-1)

[Merlin95]

Jen suis rester à ca :

Tout est dans le titre j'ai remarqué que pour n premier, en créant une suite régressive de raison 2 en partant de 2n-1, la position des premiers carrés successifs (prédécesseurs et successeurs) est un nombre premier quasi toujours et toujours si on additionne les écarts entre carrés au nombres positionnels obtenus.

Pourrais tu illustrer cela sur un exemple concret ?

[Médiat]

Bonsoir Merlin95

C'est la formule que j'ai donné au message 17 (sans tenir compte de la fin de la phrase (après "et toujours...") ), qui ne fait pas mieux que le hasard quand on fait les calculs correctement.

[invite36041331]

une petite piqûre de rappelle :

Pour éviter de parler de hasard :

entre 1 et 1299709, il y a 100 000 nombres premiers, dont 42851 pour lequel par ta méthode on obtient à nouveau un nombre premier, ce qui fait un pourcentage de réussite de 42.851 %
Dans le même temps entre 1 et 1299709 on a 649855 nombre impair dont 100 000 nombres premiers, ce qui fait un pourcentage de nombre premier parmi les nombres impairs de 15.388 %


le code source en Maple qui m'a mené à cette conclusion :

t:=0; p:=1; for i from 1 to 100000 do p:=nextprime(p);  a:=trunc(sqrt(2*p-1)); X:=a-1+(a mod 2); Y:=(2*p-1-X^2)/2+1; if(isprime(Y)) then t:=t+1; fi:od:

[invite36041331]

Entre n = 25 et n = 39...

Entre n = 2965 et n = 3119...

Je complète ma remarque en disant que les intervalles [25,29] et [2965,3119] sont dans l'intervalles [1,1299709]

[Médiat]

Je n'arrive pas à croire que Dattier, avec tous ses diplomes persistent dans une erreur que l'on trouve généralement chez les élèves de lycée.

[invite84127968]

Pour l’aparté "Modrian" les écarts en position donnent cela:



@ mediat, je ne suis pas très formule ni arithmétique des modulos donc je ne comprends pas trop à quoi correspond le termes E dans votre formule.
L'idée qui serait à retenir est que l'on peut dans la suite des premiers au travers de ce type de formule obtenir n carrés successifs pour une variable k donnée.

[pm42]

je ne suis pas très formule ni arithmétique des modulos

Pourtant, c'est assez utile quand on veut manipuler des nombres entier en général et premiers notamment...

[Médiat]

@ mediat, je ne suis pas très formule ni arithmétique des modulos donc je ne comprends pas trop à quoi correspond le termes E dans votre formule.

Il s'agit de la partie entière.
Et le peintre c'est Piet Mondrian, et come disait Dali : Piet, niet (la critique picturale la plus courte et la plus percutante connue

[invite36041331]

Je n'arrive pas à croire que Dattier, avec tous ses diplomes persistent dans une erreur que l'on trouve généralement chez les élèves de lycée.

Oui, avec tous mes diplômes, je ne connais pas de définition formelle et consensuelle du mot hasard, on dirait que toi oui.

Pourrais-tu enrichir ma culture mathématique et celle des lecteurs dans mon cas, en nous donnant cette définition formelle ?

Merci.

[Médiat]

Oui, avec tous mes diplômes, je ne connais pas de définition formelle et consensuelle du mot hasard,

Mèzalor comment avez-vous fait vos calculs et atteint la conclusion (fausse néanmoins) :

ta méthode reste en moyenne 6 fois plus bonne que le hasard.

[invite36041331]

Mèzalor comment avez-vous fait vos calculs et atteint la conclusion (fausse néanmoins) :

C'est une erreur de vocabulaire, que j'ai corriger avec mon message où je ne parle plus de hasard (le message 27)

Maintenant, veux tu bien nous dire la définition formelle du hasard que tu utilises ?

[Médiat]

C'est une erreur de vocabulaire, que j'ai corriger avec mon message où je ne parle plus de hasard (le message 27)

C'est ce que l'on peut appeler une erreur persistante :

A Good News, tu fais mieux que le hasard.

ta méthode reste en moyenne 6 fois plus bonne que le hasard.

avec ta méthode, on fait en moyenne 3 fois mieux que le hasard.

tu fais 3 fois mieux que le hasard.

Quant à moi, j'utilise les indicateurs que l'on trouve dans tous les manuels pour débuter les probabilités :

Entre n = 25 et n = 39, il y a 3 nombres premiers, La valeur calculée est comprise entre 1 et 15 qui contient 6 premiers (ou égal à 1) en appliquant la loi binomiale on a une espérance de 2.3 et un écart-type de 0.6, il n'y a donc rien d'anormal à en trouver 3 !

Entre n = 2965 et n = 3119, il y a 17 nombres premiers, La valeur calculée est comprise entre 1 et 155 qui contient 35 premiers (ou égal à 1) en appliquant la loi binomiale on a une espérance de 7.6 et un écart-type de 4.2, il n'y a donc rien d'anormal à en trouver 8 !

[invite36041331]

Quant à moi, j'utilise les indicateurs que l'on trouve dans tous les manuels pour débuter les probabilités

Sur quelle espace probabilisé travailles-tu ?

En effet les entiers peuvent être munis de tas de proba différentes à l'exception de l'uniforme ?
Laquelle as-tu utilisée pour parler de hasard ?

[Médiat]

Sur quelle espace probabilisé travailles-tu ?

Et vous ? Répondez à cette question et vous devriez trouver votre erreur.

Quant à moi, j'ai déjà répondu, cela vous a échappé ?

[invite36041331]

Entre n = 25 et n = 39, il y a 3 nombres premiers, La valeur calculée est comprise entre 1 et 15 qui contient 6 premiers (ou égal à 1) en appliquant la loi binomiale on a une espérance de 2.3 et un écart-type de 0.6, il n'y a donc rien d'anormal à en trouver 3 !

Entre n = 2965 et n = 3119, il y a 17 nombres premiers, La valeur calculée est comprise entre 1 et 155 qui contient 35 premiers (ou égal à 1) en appliquant la loi binomiale on a une espérance de 7.6 et un écart-type de 4.2, il n'y a donc rien d'anormal à en trouver 8 !

Désolé Liet Kynes, mais votre méthode ne fait pas mieux que le hasard !

Non, je vois bien quelle loi tu utilises sur les intervalles finis que tu considères, mais si cela te permet de conclure sur le "hasard" dans ces intervalles, or de ce que j'en comprends, tu conclus pour le "hasard" sur les entiers en totalité.

D'où je te repose la question, dans quel espace probabilisé travailles tu ?

Dans mon cas (message 27) c'est simplement la loi uniforme sur l'ensemble fini [1,1299709]

[Médiat]

Vous n'avez toujours pas compris (je passe sur les nouvelles erreurs de ce post)

c'est simplement la loi uniforme sur l'ensemble fini [1,1299709]

Pourquoi ? En prenant [1,1265468641354654314684314684 354384354873599709] vous auriez de meilleurs résultats.

Avec votre raisonnement je peux annoncer que je connais une méthode pour avoir pile quand je lance une pièce (de 1 euro)et dans à peu près 1 cas sur 2 alors que le calcul de la loi uniforme donnerait 1 chance sur 6 (et je pourrais trouver pire exemple, mais vous vous plaindriez auprès de la modération en pensant que je me moque)

Je suis déçu, j'étais vraiment persuadé que vous trouveriez tout seul, avec tous vos diplômes.

[invite36041331]

1/ Pourquoi ? En prenant [1,1265468641354654314684314684 354384354873599709] vous auriez de meilleurs résultats.

2/ Avec votre raisonnement je peux annoncer que je connais une méthode pour avoir pile quand je lance une pièce (de 1 euro)et dans à peu près 1 cas sur 2 alors que le calcul de la loi uniforme donnerait 1 chance sur 6.

3/ Je suis déçu, j'étais vraiment persuadé que vous trouveriez tout seul, avec tous vos diplômes.

1/ Limiter par la puissance de calcul de mon pc.

2/ Je ne sais pas de quoi tu parles, mais si on fait l'hypothèse que quand on lance une pièce on n'a que 2 possibilités pile ou face de manière équiprobable, cela donne sous cette hypothèse une proba de 1/2 d'avoir pile.
Ceci étant dit, si ta pièce à six faces (ce qui s'appelle un dé) avec une hypothèse similaire, on a 1/6.

3/ Et moi je suis déçu que tu refuses d'enrichir ma culture mathématique en précisant l'espace probabilisé sur lequel tu travailles pour parler de ton "hasard".

4/ Je précise que l'espace "naturelle" pour faire des probas, est l'espace uniforme, mais le problème c'est que cela n'existe pas sur les entier cf le lien de PLS et donc il y a plusieurs choix possible, Médiat à fait un choix (qu'il refuse de préciser) mais il y en d'autres possible, donc on peut dire, en conclusion (sauf si enfin Médiat accepte de préciser son choix d'espace probabilisé) :

La méthode proposer ici ne fait pas mieux que le hasard choisie par Médiat.

Maintenant si l'on choisie comme espace probabilisé sur les entiers P({i})=0 pour i>1299709 ou i=0, et pour i<=1299709 P({i})=a>0

Alors la méthode proposée ici fait environ 3 mieux que le hasard choisie par mes soins (cf post 27)

Bonne soirée.