Relation suite des predecesseurs impaires des premiers et position des carrés

[Merlin95]

Bonsoir Liet Kynes,

Si j'ai bien compris vos explication du message #1, vous calculez , puis et vous dites, si n est premier, alors Y est premier (souvent), mais ce n'est vrai que parce Y est impair et que pour les petites valeurs de n il y a beaucoup de premiers, mais avec n > 3000 par exemple c'est faux

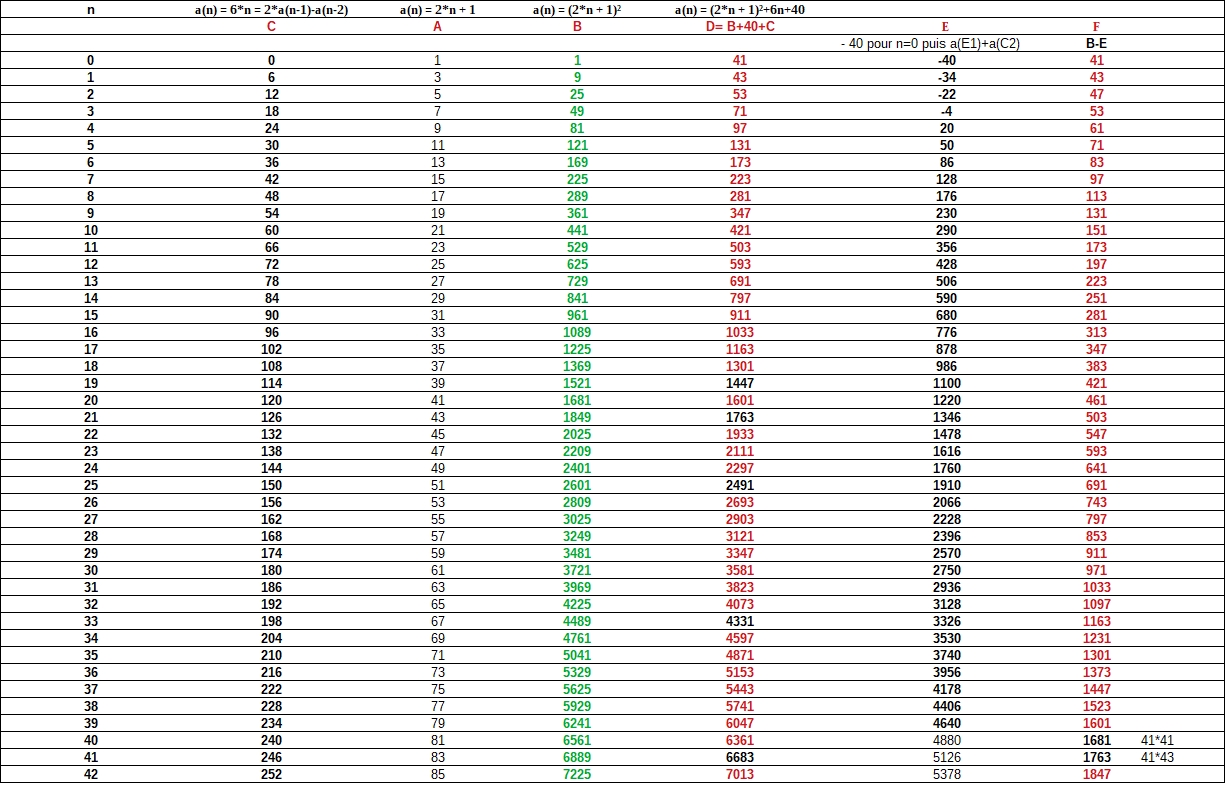
J'ai compris personnellement qu'il calcule pour n premier pour puis etc.

ensuite , , etc...
il prend le successeur et prédécesseur de , , etc.
soit les nombres
, ,
,
,

Et il remarque que la position de ces nombres sont des premiers. Mais je ne vois pas ce qu'il appelle "position".

Liet Keynes, vous pourriez apporter vos commentaires et comme je l'ai dit donner un exemple concret pas sous forme de tableau mais d'un cas unique ?
-----

[Médiat]

Bonsoir Merlin95,

Ce que j'ai compris du message N° 1 :

On part d'un nombre premier n, par exemple 139, on calcul 2n-1 (277) et on regarde les prédécesseurs impairs, jusqu'au premier carré :
277, 275, 273, 271, 269, 267, 265, 263, 261, 259, 257, 255, 253, 251, 249, 247, 245, 243, 241, 239, 237, 235, 233, 231, 229, 227, 225= 15²

225 est en position 27 dans cette liste (pas de chance, il n'est pas premier)

[Médiat]

1/ Limiter par la puissance de calcul de mon pc.

A défaut d'être la meilleure, c'est la moins mauvaise raison mathématique que vous ayez donnée.

Puisque vous insistez, je vais développer, mais ne venez pas vous plaindre que je me moque.

Pour la pièce de monnaie (j'ai précisé de 1 € pour éviter que l'on me parle de pièce à 6 faces, encore une information de perdue), voilà une copie du type de raisonnement tenu par Dattier, a priori sans qu'il s'en rende compte :

Je lance la pièce: Espace des possible est :
1) pile,
2) face
3) tranche
4) la pièce tombe dans de la vase et il est impossible de la retrouver
5) la pièce tombe dans un bol d'acide rendant impossible de savoir de quel côté elle est tombée
6) un pie qui passait pas là a volé la pièce avant qu'elle n'atteigne le sol

Il y a 6 cas possibles (et on pourrait en trouver d'autres) et un seul cas favorables (pile) donc la probabilité d'avoir pile est de 1/6, et je vous assure que je sais comment faire pour avoir environ 1 chance sur 2

Dans le cas proposé par Liet Kynes, Dattier décide que les possibles sont compris entre 1 et 1299709 (sans aucune autre justification que la puissance (sic) de son pc, c'est aussi ridicule que les 6 cas pour pile ou face.

Pour comprendre quel espace probabilisé j'utilise, il suffit de regarder ce qui se passe pour les intervalles que j'ai donné.

Toujours en appliquant la méthode de calcul de Dattier, la fonction f(n) = n donne 100% de nombres premiers sur [1, 1299709] à comparer avec le "hasard" qui donne 15% (si n est impair) d'après Dattier, j'ai donc trouvé une excellente façon de déterminer si un nombre est premier.

Toujours en appliquant le même raisonnement on obtient un résultat similaire pour la fonction f(n) = 3 (je peux donner d'autres exemples si vous voulez)

[Merlin95]

Bonsoir Merlin95,

Ce que j'ai compris du message N° 1 :

On part d'un nombre premier n, par exemple 139, on calcul 2n-1 (277) et on regarde les prédécesseurs impairs, jusqu'au premier carré :
277, 275, 273, 271, 269, 267, 265, 263, 261, 259, 257, 255, 253, 251, 249, 247, 245, 243, 241, 239, 237, 235, 233, 231, 229, 227, 225= 15²

225 est en position 27 dans cette liste (pas de chance, il n'est pas premier)

Ok en effet, je comprends mieux ainsi. Merci.

[invite7b7f1ad0]

Bonsoir Merlin95,

Ce que j'ai compris du message N° 1 :

On part d'un nombre premier n, par exemple 139, on calcul 2n-1 (277) et on regarde les prédécesseurs impairs, jusqu'au premier carré :
277, 275, 273, 271, 269, 267, 265, 263, 261, 259, 257, 255, 253, 251, 249, 247, 245, 243, 241, 239, 237, 235, 233, 231, 229, 227, 225= 15²

225 est en position 27 dans cette liste (pas de chance, il n'est pas premier)

La création de la suite est bonne mais pas le choix du carré considéré, c'est un peu plus compliqué qu'il n'y parait:
Il faut chercher ceux qui possèdent un carré successeur direct ou un prédécesseur direct pour créer des "couples ", pour 139, et cet exemple est bien choisi, on s’arrête donc en position 55 pour trouver 169 (13²) car en ligne 167 on trouve 225 (15² qui est le carré impaire directement successeur de 169) ensuite en position 115 on trouve 49 pour n=137 précédé de 25 pour n=127. On obtiens deux couples de carrés (169,225) en position 55 et (25,49) en position 115 donc un couple de positions (55,115) et un couple de carrés considérés pour repérer les positions (pour n=139; 169 en position 55 et 49 en position 115).
L'exemple de n=139 donne donc deux positions qui ne sont pas des nombres premiers, mais pour les 125 n premiers que j'ai relevé pour les positions des carrés "successeurs" il y a 101 premiers 101/125= 80.8% et 95/125 positions qui sont des premiers pour les carrés "prédécesseurs", il n'y a que 11 couples de positions dont les deux membres sont non premiers, 11/125=88%.
Le dernier % est donc : 88% des couples positionnels possèdent au moins un nombre premier. Un poil plus complexe encore: si on ajoute l'écart entre les couples de carrés "prédécesseurs" au nombres positionnels respectifs on obtiens une "statistique" disant au moins un des trois nombres est premier de 96,4% (pour n=139 on a deux couples de carrés, (25,49) et (169,225) donc deux écarts (24 et 56): je me suis intéressé à déduire ou ajouter ces écarts ou la moitié de ceux-ci etc..)
Donc pour 139 j'obtiens un premier dans cette condition "tirée par les cheveux" mais ce n'est pas cela qui m'interpelle.
Ce qui est intéressant c'est de voir que l'on peut partiellement aligner au travers de la formule générique les carrés et cela de façon successives : avec la formulation (n premier*2)-1 puis -2,-2,etc.. en position 19 sont alignés les 18 premiers carrés successifs impaires: 1,9,25...1089,1225 soit les carrés des nombres impaires de 1 à 35
Avec la formulation (n premier * 4)-3 puis -2,-2,etc.. en position 81 sont alignés les 40 premiers carrés impaires (1,9,25,49 ... 5929,6241) qui sont les carrés de 1 à 79.

@Mediat désolé d'avoir écorché Mondrian, j'ai omis effectivement N dans son nom, il eut été plus fâcheux d’omettre R d'enlever 0 est d'y mettre E la partie entière: cela donne Pi est Mediane à la place de PIET MONDRIAN

Question supplémentaire: Existe t-il dans la suite des écarts des nombre premiers un intervalle symétrique (isomorphe) plus grand que celui que j'ai décrit écarts des nombres premiers de 137 à 193: (2,10,2,6,6,4,2,10,2) ?
Je n'ai pas trouvé de méthode de recherche dans la liste des premiers avec mon tableur.

[Médiat]

Bonjour,

De ce que je comprends, la deuxième méthode de calcul joue sur la même contraction des espaces et clairement, plus l'intervalle est petit et plus la probabilité de tomber sur un premier est grande, vous ajoutez un "ou" dans votre recherche, ce qui augmente encore la probabilité de tomber sur un premier et avec un deuxième "ou", cela augmente encore.

Vous devriez vérifier si vous avez toujours 88% et 96.4% entre 638 168 661 001 et 638 170 920 503.

[invite7b7f1ad0]

Je suis bien d'accord avec vous, les statistiques obtenues ne sont pas vraiment intéressantes en soit mais que pensez vous de ces "alignements" de carrés en fonction des valeurs x et y avec x=y+1 dans la typologie de formule utilisée (n premier * x)-y puis -2...?

[Médiat]

Je n'en ai aucune idée, mettez cela sous forme de formule mathématique et je regarderai.

[invite7b7f1ad0]

J'ai tenté de faire des formules mais je ne suis pas très doué. J'ai fait un tableau ci dessous avec les formules correspondantes, pour la colonne E je ne sais pas si c'est bien formulé?
Il s'agit toujours de la position 81 avec ( (n premier*4)-3 puis -2,-2,etc), les premiers correspondant sont dans l'intervalle 41 à 1601 les carrés de 1 à 6241:

[Médiat]

Déjà la colonne D ne correspond pas à la formule !

[Médiat]

Sinon, vous avez trouvé un moyen compliqué de calculer le polynôme d'Euler : n² + n + 1

[invite7b7f1ad0]

Oups: correctif a(n) = (2*n + 1)²-6n+40 pour la colonne D.

J'ai remarqué qu'il y avait un lien avec le polynome d'Euler car les écarts sont identiques entre la colonne D obtenue et et les écarts obtenus dans le polynôme, les valeurs des nombres considérés en colonne F donnent par contre un écart qui croit de deux régulièrement. Mon tableau est valide jusqu'à n= 39 le polynome d'Euler bien plus.
C'est dans cette idée que je pense à une formule qui évolue et dont l'évolution pourrait être elle même de nature polynomiale.

[invite7b7f1ad0]

La base de ce raisonnement est dans les suites des restes de la divisions euclidienne, si on y regarde de près on trouve deux suites "imbriquées" l'une dans l'autre pour chaque nombre entier:

Restes de la division par 5 des entiers naturels pour n supérieur ou égal à 5: 0,1,2,3,4,0,1,2,3,4,0,1,2,... si je dénombre les restes et les "restes pas" cela fait 1,1,2,3,4,2,5,6,7,8,3,9,10,11,12,4,13,14...
Et de fil en aiguille j'en suis arriver à ce post.

[Médiat]

Sinon, vous avez trouvé un moyen compliqué de calculer le polynôme d'Euler : n² + n + 1

Oups, le polynôme d'Euler est n² + n +41 bien sûr

[invite7b7f1ad0]

Et n ne doit pas être que impaire dans ce polynôme sinon on reste à ma colonne D
Donc j'ai surement un petit peu compris ce à quoi pensé Euler dans mon histoire. Merci des explications !

Quand on y pense, Euler était doté d'une force de travail et d'abstraction incroyable car il ne possédait pas d'électronique pour réaliser les calculs et ce polynôme bien que paraissant simple a dû être l'objet d'un nombre incroyable de calculs "à la main"!
A l'époque le papier coutait cher en plus, la lumière était rare à la nuit tombée etc.. bref c'est phénoménale.

[gg0]

Encore plus phénoménal : Lui faisait des maths, pas des lignes de calcul "pour voir" (surtout à la fin !!).

[invite7b7f1ad0]

Encore plus phénoménal : Lui faisait des maths, pas des lignes de calcul "pour voir" (surtout à la fin !!).

Oui, je viens de parcourir l'article de wikipedia, il semble qu'il était doté d'une mémoire eidétique. Le fait, parfois, de fermer les yeux lorsque l'on raisonne est peut-être un appel à ce type de mémoire?

[gg0]

Aucun rapport avec le fait de faire des maths. Il faut déjà vouloir en faire ...

[invite7b7f1ad0]

Vouloir ne suffit pas toujours malheureusement, cela ne veut pas dire qu'il faille ne rien faire si on a de la curiosité et je ne pense pas faire non plus n'importe quoi, n'importe comment.

[gg0]

Mais si ! Vouloir faire des maths permet d'en faire vraiment ! Faire des petits calculs sans même être capable de dire ce que l'on fait exactement ne sert à rien, alors qu'avec un apprentissage minimum des mathématiques, on peut apprendre à dire ce qu'on fait. Pour l'instant, malgré la bonne volonté de divers intervenants, personne n'est vraiment sûr d'avoir compris de quoi il s'agit. Peut-être est-ce ce que suggère Médiat, mais tu es tellement flou ...

Mais ça reste une question de volonté.

[invite7b7f1ad0]

La capacité à dire et exprimer sous forme mathématique qui me manque est dans l'expression des termes. La notation et ses règles, j'ai lu l'histoire des projets de formalisation de Hilbert jusqu'à Gödel et j'ai bien retenu le concept et l'importance des définitions cependant je me retrouve souvent en tentant de rester dans le chemin à errer dans d'autres chemins buissonniers, j'ai tenté d'évoquer ce problème sous forme d'un post en évoquant une éventuelle logique basée sur l'analogie à la fois animée et motivée par un langage descriptif mais parler de maths ainsi est déjà ne plus faire des maths.
Je comprends l'importance de ce que vous dites, je me retrouve souvent à me disperser dans mes raisonnements, d'autant que je ne les notes pas faute d'en être capable. Le fil revient malgré tout à travers des traitements graphiques issus de mon tableur.
Dans ce post l'idée de départ n'était pas vraiment dans la formule d'Euler, bien que, à bien y réfléchir, j'avais déceler certaines propriétés de celle ci dans ce que j'observai, je vais rechercher mon fil de départ et le proposer en tentant de formuler et définir plus clairement. Première étape trouver une lecture sur la méthode pour définir une situation en mathématique.

[gg0]

Ça s'apprend, on appelle ça "apprendre les maths" (*).

(*) pas lire des textes sur les maths, pas lire de la vulgarisation.

[invite7b7f1ad0]

La difficulté de cet apprentissage des maths est le S de maths: comment sélectionner ce qui va être nécessaire et utile lorsque l'on a un temps limité (je n'ai plus 20 ans)?
J'ai identifié la nécessité de reprendre les notions de fonctions et d'ensembles pour l'instant.

[gg0]

le plus important est de na pas se perdre dans les notions fondamentales, surtout si on a l'esprit littéraire ou philosophique. Il faut reprendre la formation d'un élève de fin de collège et lycée pour assurer les bases d'utilisation du calcul et de ses significations. Ça permet déjà de mettre en forme des formules adaptées à ce qu'on fait.
Et c'est ce qui t'a été demandé depuis le début.

[invite7b7f1ad0]

Dans les conseils que vous donnez, vous dites souvent que les sites internet ne sont pas une bonne base de travail pour ce genre d'apprentissage, avez vous en tête un ou deux livres adaptés.
J'ai tenté d'utiliser ce site pour travailler: https://www.methodemaths.fr/ mais la forme ne me convient pas, ce n'est pas assez détaillé.

[invite51d17075]

Pour ma part, il me semblerait déjà ( et ce serait un grand pas ) de mettre simplement ces "calculs" sous forme littérale ( au sens mathématique ).
Car il est difficile ( euphémisme ) de s'y retrouver.
On fait des n²-2k , on cherche le(les ?) premier nb premiers trouvés , on fait des diffs, des additions , on manipule des colonnes.
et au final , on trouve des stats (? ) entre diffs valeurs (?)
et moi , je suis paumé.

edit : Médiat semble avoir trouvé une analogie avec qcq chose de connu.
et effectivement ça y ressemble un peu ( comme du canada dry )

[albanxiii]

Pour ma part, il me semblerait déjà ( et ce serait un grand pas ) de mettre simplement ces "calculs" sous forme littérale ( au sens mathématique ).

Ou de poster les fichiers de ce fameux tableur, car il doit bien y avoir une formule quelque part pour calculer tout ça.

Sinon, le message #80 : je suis entièrement d'accord. Ca n'est pas aux autres de décrypter ce que tente de faire Liet Kynes, c'est à lui de présenter son raisonnement et ses résultats de façon intelligible.

D'ailleurs, à défaut de formule, peut-être pourrait-on avoir le raisonnement qui permet d'obtenir tous ces nombres ?

[gg0]

On se contenterait d'une explication précise, une "recette de cuisine" qui est écrite pour être lue et comprise. Mais on a eu une "explication" floue suivie de compléments qui rendent le tout très fumeux.

[invite7b7f1ad0]

Je veux bien partager mon fichier ods mais 18 Mo avec un bordel phénoménal dedans, le risque pour celui qui s'y penche de passer des heures pour au final n'y voir qu'une trivialité navrante (cf ma découverte de la table de 101 pour ceux qui l'avaient vu), je ne sais pas si c'est une bonne idée. Partant en plus de la suite des nombres premiers, il y a pas mal de données qui sont relevées à la main. Je place en plus certains calculs là ou j'ai de la place donc la logique du type opération 1, opération 2 etc.. opération finale, n'est pas évidente.
L'analyse de Mediat est bonne, je retrouve le polynôme d'Euler via un chemin compliqué. Ma première intention était de savoir si il y avait bien ce genre de relation entre premiers et carrés, elle est donc ponctuelle.

[gg0]

OK !

Donc sujet clos.