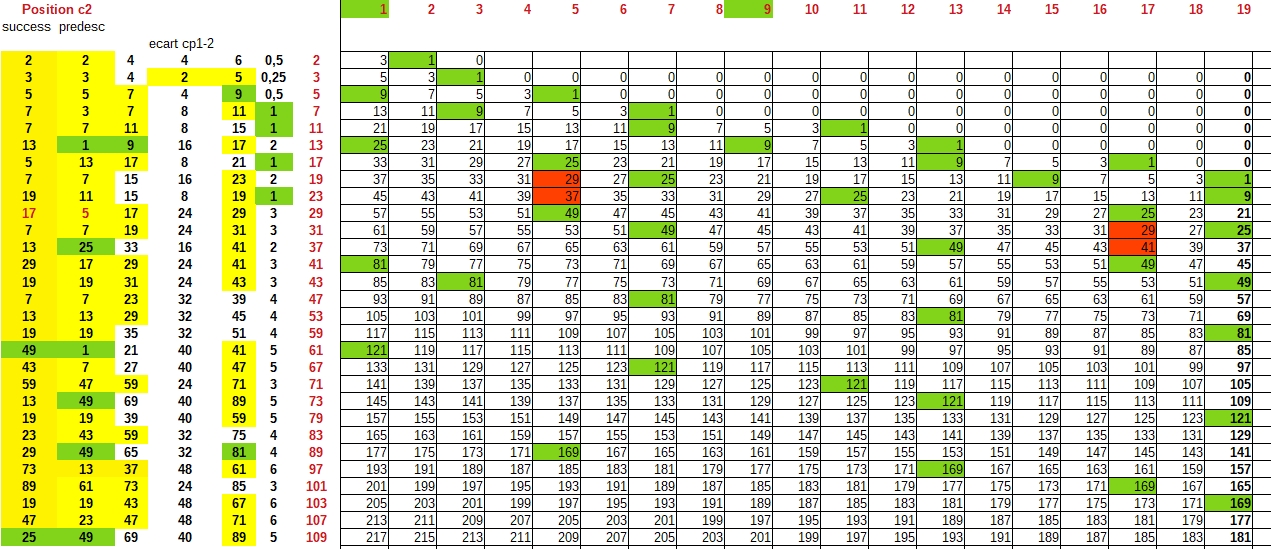
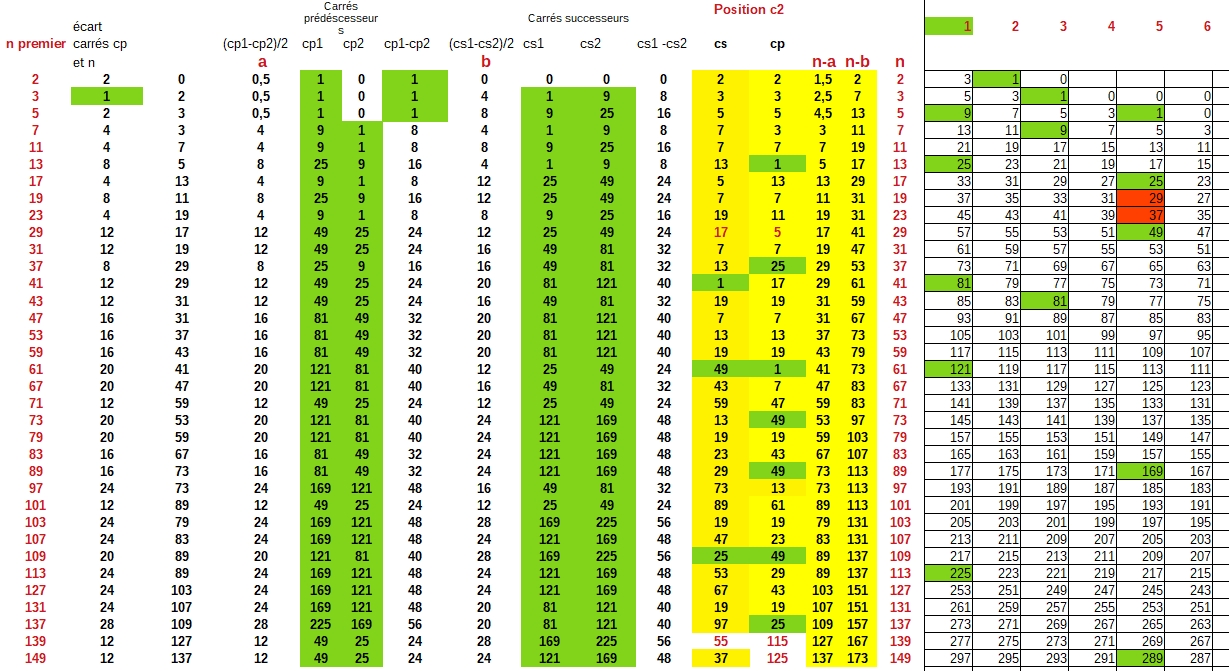
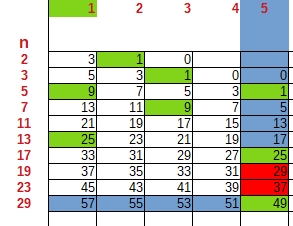
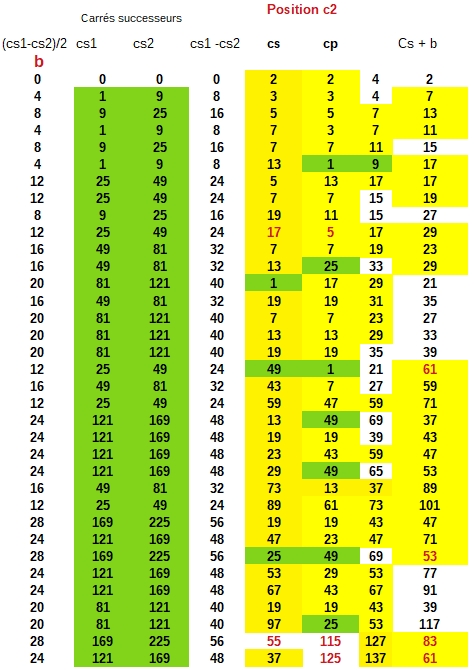
Tout est dans le titre j'ai remarqué que pour n premier, en créant une suite régressive de raison 2 en partant de 2n-1, la position des premiers carrés successifs (prédécesseurs et successeurs) est un nombre premier quasi toujours et toujours si on additionne les écarts entre carrés au nombres positionnels obtenus.
Sur l'image ci dessus: en colonne et en case rouge les carrés pour lesquels je prends en compte la position.
A noter que en position 19, les carrés se succèdent jusqu'à 1225 (35² ou 25*49), c'est la seule position qui a cette propriété que j'ai trouvé (j'ai pas cherché bien loin cela dit 509).
L'écart entre les premiers (sur l'exemple de n=29) correspondant à l'écart entre deux carrés successifs correspond à la moitié.
n=29 carrés successifs = 25/49 en position 5 et 25/49 en position 17 correspondent respectivement aux nombres premiers 17,29 et 41: 29-17= 12 et 41-29=12 pour 49-25=24.
Il y a possibilité de créer une suite "parallèle" à celle des écarts entre premiers avec cette idée.
J'espère que mon propos est bien exprimé, n'hésitez pas à me questionner si ce n'est pas le cas.
Merci de me lire en tout cas.
très franchement, plus vraiment maintenant.Envoyé par Liet Kynes
tu sembles très focalisé sur des conjectures approximatives liées aux nombres premiers. ( combien de fils et de posts ?)
en "tournicotant" des analyses diverses, tu arrives à des "trucs" qui statistiquement semblent te donner des pistes.
mais rien d'exact et de démontrable.
beaucoup sont fascinés par ces nombres ( pas moi ) et que d'encres ont déjà coulées sur la recherche de conjecture exactes.
quand aux approches qui donnent des résultats partiels, il y en a tellement qu'on pourrait presque chercher à en réinventer tlj.
bref, ( avis personnel ), tu risques de ne passionner personne avec tes démarches.
ps: mais une passion, ça ne se commande pas, et mon propos n'est pas de l'ordre d'un jugement sur la démarche.
pps : je regarderai néanmoins ta pièce jointe quand elle sera dispo pour être sur d'avoir compris, afin d'y ajouter un commentaire éventuel.
Cdt
Merci, je remet mon tableau (avec un correctif pour n=41) et j'ai remis les colonnes en ordre pour une lecture plus facile. Les n-a et n-b sont les colonnes trivialement à 100%. les deux colonnes cs et cp sont les positions des carrés successifs (= les k-ièmes). Je ne sais pas s'il est possible de calculer quelque chose je trouve cela intéressant. Dans les nombres premiers c'est les écarts qui m’intéresse, lorsqu'ils formes des séries isomorphes (écarts entre les premiers de 149 à 191 par exemple): c'est un intérêt graphique en fait que j'ai.
Mon tableau ré-organisé:
Erratum : lire n+b
je ne comprend pas comment sont calculés les cs1 et cs2 !!
Dans mon tableau pour n=19, le premier carré rencontré est 49, il est le 5 ème terme de la suite. Dans les 5èmes termes des suites précédentes on trouve 25 pour n=17. Ces deux carrés sont l'un pour l'autre successeur et prédécesseur.
Ainsi cs1 =25 et cs2 = 49 pour n=17 qui sont les mêmes termes cp1=49 et cp2=25 pour n=29.
déjà, je suis perdu.
en quoi le premier carré ?
le 5ème de quelle suite ?
En bleu dans l'extrait suivant:
Pour n (n étant un nombre premier) la suite est simple: premier terme =n*2-1, second terme= premier terme-2, troisième terme =deuxième terme-2 etc..
ça ne répond pas à ma question
On est bien d'accord sur le fait qu'il s'agit d'appliquer une régression de raison 2 sur les nombres premiers après les avoirs élevés à la valeur pour n étant premier, (n*2)-1.
On obtiens pour chaque premier une suite.
Pour n= 29: 57,55,53,51,49,47 ... etc 49 est le premier carré rencontré et il est le 5ème terme dans la suite crée à partir de n=29. pour ce carré correspond 25 en 5ème terme également mais pour n=17 (33,31,29,27,25,23..).
En repérant ces carrés successifs et notant leur position, j'obtiens un grand nombre de premiers (colonne cs et cp), (et de façon triviale les colonnes n-a et n-b sont des nombres premiers puisque l'écart entre deux carrés considérés ainsi et la somme des écarts entre les premiers de la colonne n).
Par contre si on additionne les écarts des carrés aux nombres de premiers des colonnes cs et cp (qui ne sont que des repères positionnel en quelque sorte), j'ai remarqué que l'on retrouvé aussi des premiers, ce qui amène à l'idée de relation entre ces positions des carrés et le fait que ces nombres soient premiers en grande concentration.
OK, donc si on exclus les nb forcement premiers, tu trouves statistiquement un "grand" nombre de premiers avec cette méthode.
et encore , tu as fait l'exercice sur un nb réduit au départ.
cela rejoint un peu ce que j'ai évoqué ici ou dans un autre post similaire.
des conjectures qui donnent "beaucoup" de nb premiers il y en a flores.
mais comme elles ne sont pas totalement fiables, elles sont peu utiles.
cela reste donc uniquement "fun" pour les passionnés.
d'autant qu'on sait déjà tous les énumérer dans l'ordre , mais pas avec ce type de démarche.
Je comprends bien ton propos et le partage, surtout sur l'idée de faire des statistiques. Je ne tire pas de conclusions de mes observations cela n’aurai pas de sens . Le fait qu'il y est une forme d'organisation émergente m'a intéressé.
Par exemple, la position 19 (19ème terme) génère 19 carrés qui sont les 18 premiers carrés impaires et 0 le premier carré paire (0,1, ...,1525) et tout ces carrés sont à la fois cs et cp, Cela m'a fait envisager l’existence d'une relation particulière entre carrés et premiers dans cette structure de suites.
a
J'essaie de comprendre. A quoi correspondent les couleurs verte, rouge et bleue ?
Pourrais tu expliquer en francais avec un exemple à l'appui, ca sera une étape préalable nécessaire pour comprendre ton tableau, si c'est bien sur celui-ci qui est illustrer apparemment une statistique intéressante ? (d'abord sur le premier tableau et ensuite sur les deuxième).
Dernière modification par Merlin95 ; 14/10/2019 à 21h35.
Bonsoir,
Juste pour redonner du courage dans ces recherches à Liet Kynes, pas besoin de démonstration* pour casser RSA (factorisation), une conjecture bien sentie suffirait, il suffit que ta conjecture soit suffisamment robuste pour être employé pour casser RSA.
* : la démonstration serait de casser avec ta conjecture certaines occurrences du problème RSA.
Bon courage.
Bonsoir Liet Kynes,
Si j'ai bien compris vos explication du message #1, vous calculez, puis
Dernière modification par Médiat ; 14/10/2019 à 23h11.
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
Précision : Y est impair pour n impair (ce qui est souvent le cas des premiers)
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
je ne vois pas très bien le lien ( même si l'approche peut ressembler de très loin ).
aparté : je ne comprend pas "casser RSA", ni quelle serait cette conjecture.
mais comme tu sembles vouloir étaler tes connaissances sur le sujet, tu peux nous faire partager tes lumières .... dans un autre post serait mieux.
L'algorithme RSA se base sur la.decomposition en facteurs premiers d'un nombre, donc si on trouve une statistique permettant de prévoir à peu près quels nombres premiers composent la.clé on peut la décomposer plus rapidement et la casser. J'explique en gros avec les mains en pratique c'est certainement un peu plus compliqué. Mais je doute qu'on puisse trouver une statistique sur les nombres premiers aussi facilement que pourrait le faire un non expert comme le PP.
Dernière modification par Merlin95 ; 15/10/2019 à 12h53.
je sais à peu près de quoi il s'agit.
ce sont les expressions employées ( par Dattier ) que je ne trouve pas claires.
En substance : "yakafocon" ! mais quoi ?
Bonjour,
A Good News, tu fais mieux que le hasard.
En effet si on prend un entier premier entre 1 et 2^30 (à peu prés 1 milliard), alors la proba que ta construction soit un entier premier est d'environs 30% (1) alors même qu'on a 5%(2) de nombre premiers dans cette tranche.
(1) : j'ai fait un petit programme en Maple pour le vérifier, je mets ici le source.
(2) : obtenue avec le théorème des nombre premiersCode:t:=0; for i from 1 to 10000 do x:=nextprime(rand(1..2^30)()); a:=trunc(sqrt(2*x-1)); X:=a-1+(a mod 2); Y:=(2*x-1-X^2)/2+1; if(isprime(Y)) then t:=t+1; fi:od: t; 2886
PS1 : il y a quand même un bémol, plus on tape dans des grands nombre premier plus cela se dilue, mais ta méthode reste en moyenne 6 fois plus bonne que le hasard.
PS2 : Je ne suis pas dans le "yakafonkon", mais dans le "c'est fait et c'est à saluer"
Bonne journée.
Si on tient compte de cette précision, avec ta méthode, on fait en moyenne 3 fois mieux que le hasard.Précision : Y est impair pour n impair (ce qui est souvent le cas des premiers
Faire ce que fait Liet Kynes, juste pour lui rappeler s'il en doutait que son travail ne sert pas à rien, et peut mener à de grande percé en arithmétique et tous cela sans faire la moindre preuve.
N'étant pas du genre à affirmer du vent comme certains :
Entre n = 25 et n = 39, il y a 3 nombres premiers, La valeur calculée est comprise entre 1 et 15 qui contient 6 premiers (ou égal à 1) en appliquant la loi binomiale on a une espérance de 2.3 et un écart-type de 0.6, il n'y a donc rien d'anormal à en trouver 3 !
Entre n = 2965 et n = 3119, il y a 17 nombres premiers, La valeur calculée est comprise entre 1 et 155 qui contient 35 premiers (ou égal à 1) en appliquant la loi binomiale on a une espérance de 7.6 et un écart-type de 4.2, il n'y a donc rien d'anormal à en trouver 8 !
Désolé Liet Kynes, mais votre méthode ne fait pas mieux que le hasard !
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
Sur ce que j'ai testé (entre 1 et 1 000 000 000), tu fais 3 fois mieux que le hasard.
Crois qui tu veux, mais juste ne te décourage pas.
Bon courage.
Pour éviter de parler de hasard :
entre 1 et 1299709, il y a 100 000 nombres premiers, dont 42851 pour lequel par ta méthode on obtient à nouveau un nombre premier, ce qui fait un pourcentage de réussite de 42.851 %
Dans le même temps entre 1 et 1299709 on a 649855 nombre impair dont 100 000 nombres premiers, ce qui fait un pourcentage de nombre premier parmi les nombres impairs de 15.388 %
le code source en Maple qui m'a mené à cette conclusion :
Code:t:=0; p:=1; for i from 1 to 100000 do p:=nextprime(p); a:=trunc(sqrt(2*p-1)); X:=a-1+(a mod 2); Y:=(2*p-1-X^2)/2+1; if(isprime(Y)) then t:=t+1; fi:od:
Bon courage.
Voilà qui devrait, même si j'ai pas tout compris, calmer les velléités de Liet Keynes de rechercher quelque chose de révolutionnaires à propos de la répartitions des nombres premiers.
Liet Kynes : Je ne doute pas un instant qu'avec tous ses diplomes, Dattier finira par comprendre son erreur (courante au lycée), mais je ne sais pas en combien de temps, si vous avez des questions, n'hésitez pas (je n'élimine pas l'hypothèse que j'ai mal compris votre message n° 1, je n'ai pas regardé vos images).
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
Merci de tout vos commentaires, (@mediat; vous connaissez ma tendance à bournifler)
Je rajouterai un petit carré à la suite des carrés de n=19 : les écarts des premiers correspondant avec leur prédécesseurs( prédécesseurs dans la suite ordonnée des nombres premiers) est de 100:
il n’existe, de ce que j'ai vue que 2 suites de 19 termes de premiers (cette fois écarts et premiers inclus dans la suite ordonnée des nombres premiers) de 79 à 173 et de 83 à 179 (on notera l'écart de 100 du coup entre la somme des premiers de ces deux suites).. voilà ces 3 suites:
100.jpg
En jaune j'ai surligné ce que je cherche particulièrement: en fait je dois surement avoir un fil (débranché éventuellement) dans ma démarche et je prends le temps de lire ce qui est accessible en langage mathématique certaines choses que je croise mais ce n'est pas langue maternelle . Mon chemin est très intuitif même si avec le temps je lui trouve une certaine continuité.
Je m'aide beaucoup du site de Gérard VILLEMIN pour donner un nom à ce que je rencontre: http://villemin.gerard.free.fr/GVCV.htm
Ce que Je cherche est une structure isomorphe dans les écarts entre nombre premier qui puisse m'amener à développer graphiquement cela :
Pièce jointe 397089
Ce damier est fait de l'intersection des nombres premiers (en rouge les jumeaux) de la suite des entiers naturels ordonnés croisée avec elle même (en ordonnée et en abscisse N, si j'ai bien compris). Voilà mon chemin intuitif: je pense à une structure qui se développe un peu comme un fractale mais toujours différemment.. S'il existe une formule, elle doit être de nature changeante, le truc serait de voir ce changement, de trouver les variables qui changent (à mon avis purement spéculatif, 3 variables) et de pouvoir calculer l'endroit exacte.. le résultat graphique doit être d'une harmonie sublime.
Des structures que je découvre je ne fait que produire des graphies:
Ici sur fond de nombre premiers, le visage de la formule magique ou l'ampoule qui contient le filament recherché (au choix) en l'état actuel des connaissances :
X.jpg
Bref, Je poursuis ma quête, le but est d’aligner les carrés maintenant.
