équation différentielle du 2nd ordre avec condition

[invite71e3cdf2]

Bonjour,

Peut-on résoudre une équation différentielle du second ordre avec une condition aux limites de la fonction recherchée, genre :



avec la fonction recherchée et la valeur de la fonction à l'abscisse

Merci d'avance
-----

[gg0]

Bonsoir.

je ne comprends pas trop ... Si L est connu, ainsi que y(L), ton équation est y"+y=Cte où la constante est -y(L). Si Y(L) est inconnu, quelle est l'équation ?

Cordialement.

[invite71e3cdf2]

je ne connais pas y(L).
en fait c'est un peu le serpent qui se mord la queue : j'ai besoin de y(L) pour résoudre le système mais je ne connais y(x).

en gros, je cherche l'équation de la flèche d'une poutre et j'ai besoin de la valeur de la flèche en bout de poutre pour la connaitre

[invite51d17075]

bsr,
donc la mise en équation du départ vient d'un exercice de physique.
il semble souhaitable de connaitre cet exercice afin que le L ne soit pas un illustre inconnu tel qu'il est présenté ici.
Cdt

[A voir en vidéo sur Futura]

[gg0]

A priori,

il y a d'autres équations en cause.

[invite71e3cdf2]

merci de vos réponses
j'ai peut être mal posé mon problème, je vais revérifier, mais les simulations numériques me confortent dans la bonne mise en équation....

[Médiat]

Bonsoir,

Vous êtes sûr que ce n'est pas plutôt j'ai mis plus ou moins sur la constante car je n'ai aucune idée de la bonne réponse

[Biname]

Salut,

Elle est où la condition du titre ?

Sejam

[JJacquelin]

@ Infra_Red
Bonjour,
y''(x)+y(x)+y(L)=0 est une équation différentielle du second ordre. Par conséquent elle a une infinité de solutions qui dépendent de deux constantes arbitraires. Ces deux constantes resteront indéterminées tant que l'énoncé du problème ne donnera pas deux conditions bien spécifiées à respecter pour trouver la solution particulière qui satisfait à la fois l'équation différentielle et les deux conditions (qui actuellement manquent dans l'énoncé).

Le titre de ta question parle d'une condition. Donc il en manquerait encore une. Mais ce que tu donnes n'est pas une condition bien spécifiée. En effet y(L) serait bien spécifiée si à la fois L et la valeur de y(L) étaient connues. Ce qui n'est pas le cas ainsi que tu le précises bien. Donc, en fait, les deux conditions manquent.

Ainsi dans l'état incomplet de l'énoncé du problème tu peux seulement espérer obtenir la solution générale avec deux constantes indéterminées. Rien de plus.

La solution générale est : y(x)=y(L)*(2*cos(x-L)-1)+C*sin(x-L)

Les deux constantes restant indéterminées sont C et y(L).

[JJacquelin]

Ajout à mon message précédent :

Tu notes que : "en fait c'est un peu le serpent qui se mord la queue : j'ai besoin de y(L) pour résoudre le système mais je ne connais pas y(x)."
Non, ce n'est pas ce qui manque. En fait, ce qui manque est la mise en équation (la modélisation) complète du problème qui, si elle était bien terminée et bien énoncée permettrait de déterminer à la fois les deux constantes, donc de déterminer y(L).

[invite71e3cdf2]

bonjour à tous,

Je n'ai pas été clair dans mon premier post, je vous pose donc le problème entier. Le problème est que maintenant ça n'a plus rien à faire dans la catégorie math

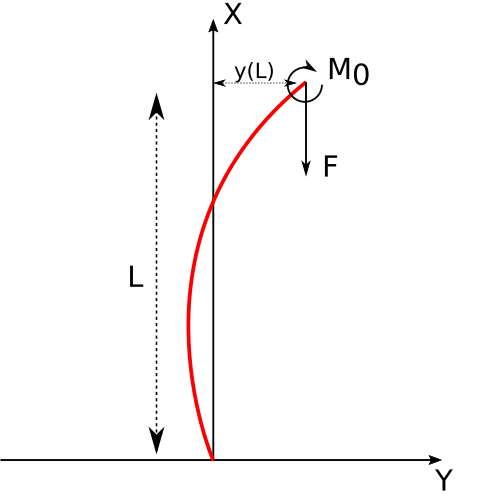
j'ai une poutre d'axe x dont la flèche y(x) est régit par l'équation :

Le moment est de la forme :

avec :
l'amorce de la flexion à l'abscisse L de la poutre
l'effort de compression à l'abscisse L de la poutre
la flèche à l'abscisse L de la poutre (inconnue !!)
la flèche le long de la poutre (inconnue !!)


j'ai donc l'équation différentielle suivante : avec comme conditions aux limites :



ma fonction inconnue est , or j'ai besoin de sa valeur à l'abscisse L pour la trouver.
Ma question est simple : peut-on résoudre ce type d'équation différentielle ?

Je suppose qu'on ne peut pas la résoudre comme cela, peut-être en passant par des séries de Bessel ??

[Biname]

Quelle est l'origine de L, 0 ou x ?

Biname

[invite51d17075]

Quelle est l'origine de L, 0 ou x ?

Biname

oui, un petit schéma ???

[invite71e3cdf2]

voila le dessin :

[invite71e3cdf2]

c'est un problème de mécanique non linéaire, donc il faut connaître un peu la mécanique.
La mise en équation pour moi est valable car est corrélée avec les simulations éléments finis.

Mon problème réside dans la résolution mathématique de l'équation ci-dessus.

J'ai un exemple de résolution d'un problème presque similaire mais avec des fonctions de Bessel.
J'aimerai ne pas en arriver là.

[invite51d17075]

d'après ton dessin y(L) est celui que l'on veut. ( il pourrait être nul )
ce qui change , c'est le xMax.
ou bien un truc m'échappe ?

[invite71e3cdf2]

en fait peu importe la longueur de la poutre, dans un problème de flambement la poutre est affectée d'une longueur virtuelle fonction des conditions aux limites.
Par contre, je viens de tilter, j'utilise des équations posées dans le cadre des petites perturbations. Or je suis dans le cas des grandes perturbations.

Je pense être hors cadre.

Bref, je pollue pas plus longtemps le forum des matheux je pose mon problème en physique

[JJacquelin]

Pourquoi as-tu oublié de donner les conditions aux limites y(0)=0 et y'(0)=0 dans l'énoncé original du problème ?
C'est cela qui manquait. Et encore faudrait-il que ces conditions soient correctes. Pour y(0)=0 pas de difficulté. Mais pour y'(0)=0 on peut être dubitatif car on voit sur la figure que la courbe tracée en rouge ne satisfait pas cette condition.
Remarque : Je n'ai pas vérifié la modélisation physique après les nouvelles informations données. Donc je ne donne aucun avis sur l'exactitude ou non de ton équation différentielle.

[Biname]

Salut,

en fait peu importe la longueur de la poutre, dans un problème de flambement la poutre est affectée d'une longueur virtuelle fonction des conditions aux limites.
Par contre, je viens de tilter, j'utilise des équations posées dans le cadre des petites perturbations. Or je suis dans le cas des grandes perturbations.

Oui mais on oublie facilement !

Je pense être hors cadre.
Bref, je pollue pas plus longtemps le forum des matheux je pose mon problème en physique

Il m'amuse moi ton problème et si Ansset ne dit rien, c'est kosher forum.
D'un point de vue physique (RDM), le flambage requière une excentricité de la charge ou ..., sans quoi, il ne 'démarre' pas, y(L)=0 doit donc être rejeté.
En plus, à la base de la poutre devrait se trouver un encastrement qui lui contrerait le moment de F : ton -F.y(x) ?

Biname

[invite71e3cdf2]

oui c'est un encastrement, le dessin n'est pas exhaustif
F(y(L)-y(x)) est le moment tout le long de la poutre et vaut 0 à y(L) et est maximum à l'encastremet

[invite71e3cdf2]

Pourquoi as-tu oublié de donner les conditions aux limites y(0)=0 et y'(0)=0 dans l'énoncé original du problème ?
C'est cela qui manquait. Et encore faudrait-il que ces conditions soient correctes. Pour y(0)=0 pas de difficulté. Mais pour y'(0)=0 on peut être dubitatif car on voit sur la figure que la courbe tracée en rouge ne satisfait pas cette condition.
Remarque : Je n'ai pas vérifié la modélisation physique après les nouvelles informations données. Donc je ne donne aucun avis sur l'exactitude ou non de ton équation différentielle.

non non je n'ai pas oublié, faut juste lire

[Biname]

Salut,

oui c'est un encastrement, le dessin n'est pas exhaustif
F(y(L)-y(x)) est le moment tout le long de la poutre et vaut 0 à y(L) et est maximum à l'encastremet

F.y(L) = M0 et msg #11 Mx = M0 - F.y(x) non ?
Et alors : EIy''(x) + Fy(x) - M0 = 0
https://www.wolframalpha.com/input/?...x%29+-+c+%3D+0

Biname pas trop sur de lui

[Biname]

F.y(L) = M0 et msg #11 Mx = 2M0 - F.y(x) non ?
Et alors : EIy''(x) + Fy(x) - 2M0 = 0

Pour x=0 y=0 et Mx = 2M0 OK
Pour x=L et Mx=2M0 - M0=M0 OK

Et EIy''(x) + Fy(x) - 2M0 = 0
https://www.wolframalpha.com/input/?...%29+-+2c+%3D+0

C'est bon là, non ?

Biname

[invite51d17075]

Slt,

S
Il m'amuse moi ton problème et si Ansset ne dit rien, c'est kosher forum.

C'est quoi "kosher forum" ?
sinon ansset était parti vaquer, , et ( outre sa boulette du y(L)=0 ) replonge à l'instant dans sa vieille physique.

[JJacquelin]

@Infra_Red :
Je ne vois pas dans ta question #1 à quel endroit est spécifiée la condition $y'(0)=0$. De plus, tu donnes un schéma qui est cause de malentendu car ne correspondant pas à un encastrement à x=0 (ce que l'on apprend beaucoup trop tard). Ce n'est pas très sérieux. Donc je me retire de cette discussion mal partie dès le départ. Bonne continuation.

[Biname]

Salut,

@Infra_Red :
Je ne vois pas dans ta question #1 à quel endroit est spécifiée la condition $y'(0)=0$. De plus, tu donnes un schéma qui est cause de malentendu car ne correspondant pas à un encastrement à x=0 (ce que l'on apprend beaucoup trop tard). Ce n'est pas très sérieux. Donc je me retire de cette discussion mal partie dès le départ. Bonne continuation.

Paske s'il aurait su, il aurait pas venu.

Sejam

[invite71e3cdf2]

@Infra_Red :
Je ne vois pas dans ta question #1 à quel endroit est spécifiée la condition $y'(0)=0$. De plus, tu donnes un schéma qui est cause de malentendu car ne correspondant pas à un encastrement à x=0 (ce que l'on apprend beaucoup trop tard). Ce n'est pas très sérieux. Donc je me retire de cette discussion mal partie dès le départ. Bonne continuation.

je pense qu'on perd tous notre temps dans cette discussion.
La méca n'a rien à voir la dedans (encastrement, pivot, ....) on s'en fiche.
ma question première était de savoir si ce genre d'équation était résolvable :


avec y(x) l'équation à trouver et y(a) la valeur de l'équationà une abscisse particulière

Il faut croire que non puisque ça ne parle à personne !!

merci à tous pour votre temps passé

[gg0]

JJacquelin t'a répondu. A voir la suite, ça ne t'arrangeait pas.

[Biname]

Salut,

Wolfram ne trouve pas de solution pour y"(x) - y(x) = y(a)
il répond "Not an ordinary ?___FIRST___? order differential equation"
https://www.wolframalpha.com/input/?...%29%3Dy%28a%29

Point de vue RDM :
https://fr.wikipedia.org/wiki/Flambage
y(L) est une condition aux limites et n'entre pas dans l'équation.
L'équation différentielle est du type : a y"(x) + b y(x) + c = 0
je doute juste pour M0 ou 2M0

Biname

RDM fleche : https://en.wikipedia.org/wiki/Deflection_(engineering)

[invite51d17075]

c'est ce que j'ai regardé en premier ( équation du dernier lien), sauf que celà s'applique qu'aux faibles déformations.
de plus la force n'est pas orientée perp à la tige ici.
je me demande s'il ne faut pas intégrer de bas en haut en appliquant la formule de cisaillement à chaque élément infinitésimal.