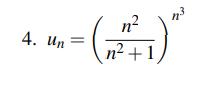bonjour jai rencontre un probleme en cherchons la nature de cette serie
bonjourj'ai rencontre un probleme en cherchons la nature de cette serie (convergente ou divergente): u(n)=((n^2)/(n^2+1))^n^3
jai dabord la regle de cauchy jai fait la racine n de u(n) mais la limite est e- 1 dans ce cas on peut pas conclure que la serie u (n) converge
mais quand jai chercher le devellopement assymptotique(2 eme methode) de u (n) en+ infini avec u(n)= (1-1/(n^2+1))^n^3
c est 1-n^3* 1/(n^2+1)+°(1/n^2+1)
la limite de ce develloppement en+ linfini est -infini donc un diverge grossierement
merci de m indique la methode la plus juste et ou est la faute exactement dans la methode fausse
-----