Dérivation d'une distribution

[gg0]

Je reprends mon message, pour corriger une autre faute de frappe, et le rendre plus facile à traiter

L'égalité est différente :
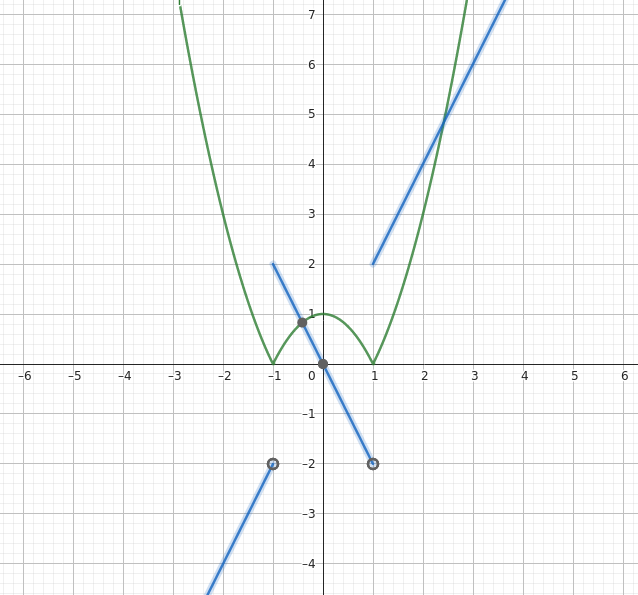
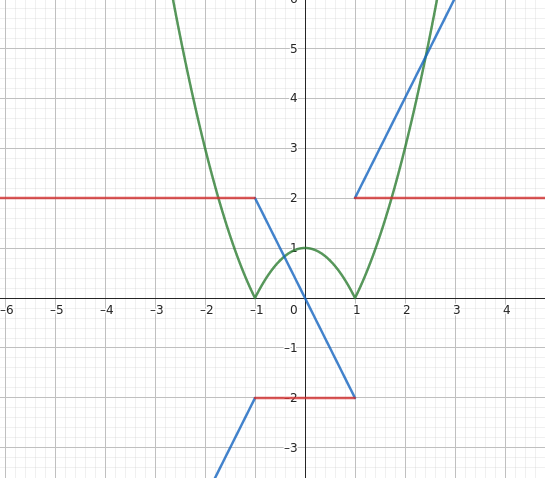
|x²-1|= (x²-1)Y(-(x+1))-(x²-1)(Y(x+1)-Y(x-1))+(x²-1)Y(x-1) (rectification de la faute de frappe)

Traduction : |x²-1| vaut
* x²-1 si x<-1
* -(x²-1) si x est compris entre -1 et 1
* x²-1 si x>1
Je t'invite à représenter sur un brouillon les fonctions qui à x associent Y(x-1), Y(x+1), (Y(x+1)-Y(x-1)) et Y(-(x+1)), puis (x²-1)Y(-(x+1)), -(x²-1)(Y(x+1)-Y(x-1)) et (x²-1)Y(x-1) (niveau de difficulté : lycée) et enfin de voir pourquoi la somme des trois dernières donne bien le bon résultat.
-----

[lesurveilleur]

Je suis un élève en L3 physique qui suit un cours de maths associé à la physique.

Voici le plan du cours que je suis en classe :

Z.png
Y.png

J'ai lu par ailleurs ce cours (la partie sur les distributions) :

X.png

@gg0 J'ai tracé tes distributions sur desmos.com mais je vois pas l'idée directrice dans tes calculs...
Comment as tu eu l'idée de considérer : (x²-1)H(-(x+1))-(x²-1)(H(x+1)-H(x-1))+(x²-1)H(x-1)

[gg0]

C'est ce que je faisais avec des étudiants de première année d'IUT, pour les transformées de Laplace.
H étant nulle avant 0 et égale à 1 après, H(x)f(x) annule f sur R- et la conserve sur R+. H(x-a) fait la même chose avec a à la place de 0, et je te laisse trouver comment annuler après a, sans changer avant. Enfin H(x-a)-H(x-b), pour a<b annule en dehors de [a,b].
Il n'était pas difficile de voir que la courbe de |x²-1| est composée de trois parties lisses, une avant -1, une entre -1 et 1 et une après 1, puis d'adapter pour avoir les bonnes expressions sur chaque morceau.

Mais sur un cours pour physicien, il doit y avoir des méthodes pour dériver les distributions, c'est quand même du travail de base.

[stefjm]

Il y a !
Théorème 36 (Formule des sauts). Soit f C1 par morceaux... page 52

Et du coup, il n'y a même plus besoin de la fonction de Heaviside si on a droit à ce théorème pour dériver les fonctions continues par morceaux.

Sinon, on peut toujours utiliser la dérivée des distributions en faisant apparaitre des h(t) retardés et/ou avancés.

[stefjm]

C'est ce que je faisais avec des étudiants de première année d'IUT, pour les transformées de Laplace.

Me too.
Mais cela devient difficile...
Même les aspects graphiques sont difficiles.

https://www.wolframalpha.com/input?i...8x%5E2-1%29%27

[stefjm]

@lesurveilleur
Vous me confirmez par MP que vous ne lisez pas les réponses qu'on vous fait ici.
La dérivée de abs(x^2-1) comporte deux sauts.

[lesurveilleur]

Ok je parlais de abs(x^2-1) pas de sa dérivée....

[lesurveilleur]

je tente :

x'+4*delta0 + (-x)'+4*delta0 +x'=1+4*delta0-1+4delta0

[stefjm]

Il n'y a rien qui va!
Vous additionnez des morceaux de fonction défini par morceaux.
Les 4*delta sont en -1 et +1.

Pour la partie dérivable :
Soit vous travaillez par intervalles, soit vous utilisez la fonction de Heaviside ou la fonction signe, soit vous utilisez la fonction valeur absolue (et la fonction signe).

Puis vous ajoutez les diracs à la partie régulière.

[lesurveilleur]

On a pour la première "bissectrice" y=x avec un saut de 4.
Pour la deuxième bissectrice y=-x avec un saut de 4.

Il n'y a pas de translation.

Donc x' +4delta0 -x' + 4delta0 = 0+8delta0...

Qu'est ce qui ne va pas ?

[stefjm]

Les deltas ne sont pas en 0.
On a y=x ou y=-x selon les intervalles.
Pas possible de tout additionner comme cela...

[lesurveilleur]

Les delta sont en-2 et +2 donc c'est delta(x+2)+1
Delta(x-2)+1

Pour la partie centrale je vois pas comment faire. Si ce n'est que la partie régulière vaut-x

....

[stefjm]

Vous confondez l'axe des abscisses avec celui des ordonnées.
En plus de me contredire!
C'est quand même fort...

D'ailleurs, on parle de quelle fonction?
La dérivée première de abs(x^2-1) est continue sauf en x=-1 et x=1, donc pas de delta sur cette dérivée.

Il y a des delta sur la dérivée seconde.

[lesurveilleur]

Donc je fais juste 2x'-x' ?

[gg0]

Il faudrait arrêter d'écrire n'importe quoi !

Quelle est la fonction dérivée de x-->|x²-1| ? Écris-la tout calcul fait.

[lesurveilleur]

|x²-1| :
a. x²-1 si x<-1
b. -(x²-1) pour x entre -1 et 1
c. x²-1 si x>1

a. 2x
b. -2x
c. 2x

Avec les bornes explicités plus haut.

Mais est-ce pareil au sens des distributions ?

[stefjm]

Ouf.
Oui, c'est pareil dans le cas de fonctions dérivables par morceaux.

La dérivée seconde maintenant. C'est elle qui présente des diracs.

[gg0]

La seule nouveauté avec les distributions, c'est qu'on passe de "pas dérivable en -1 et 1" à "rien de particulier en -1 et 1", une distribution n'ayant pas de "valeur en a".

[lesurveilleur]

Je sais que le saut est de 4...

De plus, y=2 puis -2 puis 2Donc :
2'+delta0*4 - (2'+delta0*4)+2'

[gg0]

Peux-tu écrire des vrais calculs, pas deux idées rédigées absurdement ? "y=2 puis -2 puis 2" c'est n'importe quoi !! Tu n'as jamais appris la notion et la notation de fonction ???? La suite est pire, 1' ne veut rien dire, et on ne sait même pas de quoi tu, parles, tu ne le dis pas.

On ne peut pas t'aider tant que tu refuses d'écrire les maths.

[lesurveilleur]

Pour -00<x<-1 f(x)=2
Pour -1x<1 f(x)=-2
Pour +1<x<+00 f(x)=2

Or, f''(x)= f(x)+delta0*(Saut)

Donc, f''(x)=(2+delta0*(Saut)) - (2+delta0*(Saut))+(2)

Où, Saut = 4..

(2+delta0*(4) -(2+delta0*(4)+(2)

[gg0]

C'est toujours du n'importe quoi ! tu n'arrives même pas à écrire correctement -1<x<1. Et f''(x)= f(x)+delta0*(Saut) est évidemment faux. D'ailleurs, on ne sait même pas qui est f !!!

Est-ce utile de continuer ?

[lesurveilleur]

Posons : f(x)=|x**2-1|


Pour -00<x<-1 f(x)=2
Pour -1<x<1 f(x)=-2
Pour +1<x<+00 f(x)=2

Or, f''(x)= f''(x)+delta0*(Saut)

Donc, f''(x)=(2+delta0*(Saut)) - (2+delta0*(Saut))+(2)

Où, Saut = 4..

(2+delta0*(4) -(2+delta0*(4))+(2)

J'ai corrigé les fautes.


@gg0 : On est toujours l'imbécile de quelqu'un d'autre pas la peine de te moquer de moi comme ça...

[stefjm]

Posons : f(x)=|x**2-1|
Pour -00<x<-1 f(x)=2
Pour -1<x<1 f(x)=-2
Pour +1<x<+00 f(x)=2

OK pour la partie régulière de la fonction.

Or, f''(x)= f''(x)+delta0*(Saut)

Tu notes pareil la distribution et la fonction régulière, c'est casse gueule!

Donc, f''(x)=(2+delta0*(Saut)) - (2+delta0*(Saut))+(2)

Mais ça , c'est nawak total! Tu additionnes encore en mélangeant les valeurs sur les différents intervalles!

(2+delta0*(4) -(2+delta0*(4))+(2)

Ok pour les saut de -4 et +4, mais ils ne sont pas en 0, comme je te l'ai déjà signalé.

@gg0 : On est toujours l'imbécile de quelqu'un d'autre pas la peine de te moquer de moi comme ça...

Personne ne se moque. Le sujets n'est pas si facile, mais tes soucis viennent de bien avant ce cours.

Un dirac en x=1 se note ou .

[lesurveilleur]

Je rappel :



Au risque de me tromper je multiplie par f'(x) en tenant comptes des différents intervalles...

f''(x)=(2+2*x*delta(x-1)*4 - (2-2*x*delta(x+1)*4+2x*2)

sigma(f')

[stefjm]

La partie régulière est fausse. 3 fois que je te le signale.
{f''}=2-2+4x ne donne pas le créneau 2, puis -2, puis 2.

Je ne comprend pas non plus pourquoi tu multiplies tes delta par 2.x.
Le théorème parle d'un saut de la fonction qu'on veut dériver à multiplier par delta au point de saut.

[lesurveilleur]

Ok donc on enlève les 2x. Et on change la partie régulière.

L'idée est de reprendre les calculs de dérive de |X**2-1|. Mais c'est ça qui fait apparaître les 2x...

[stefjm]

C'est pour f' qu'on a +-2.x selon l’intervalle.
Pour {f''}, on a des +-2 selon l'intervalle.

[lesurveilleur]

J'avais pas vu ton message je te réponds

[lesurveilleur]

(2+4*delta(x-1) )-(2+delta(x))+(2+delta(x-1)*4)