un petit problème pour les vacances

[GBZM]

J'ai déposé les marques "rue" et "avenue". Prière de ne pas tout embrouiller en fabriquant des contrefaçons.

Un dominosa avec une rue (en vert) et deux avenues (en rouge).
rueavenue.png
-----

[Liet Kynes]

Ben oui mais tes rues ne sont pas celles décrites par MissJenny, tu changes le problème, c'est quand même clair que ce qui est recherché c'est la probabilité d'avoir au moins un alignement horizontal de dominos d'après l'énoncé.

"Quand on a résolu le problème, on voit qu'il y a deux sortes de configuration : celles où une "rue" rectiligne apparaît qui traverse tout le tableau, et celles où il n'y a pas de telle traversée. Les images jointes montrent les deux types de configuration."

Dans les 2 exemples mis en PJ par MissJenny, "dominosa sans traversées" il y a celui là qui comporte deux rues selon ta définition, ce qui prouve qu'une traversée est un alignement de dominos et l'exemple avec traversé est alignement de dominos horizontaux à noter que le fait qu'il n'y a qu'un seul exemple "avec traversée" implique que l'on considèrera dans ce problème que les alignements horizontaux (sinon MissJenny aurait mis un exemple avec traversée verticale en plus) :

[Biname]

C'est clair, Biname ne sait pas lire. Recopier in extenso un message que j'ai écrit, ce n'est pas lire (et ça ne sert à rien d'autre qu'à alourdir le fil).
Mais je ne suis loin d'être le seul objet de cette incompréhension : Biname n'a pas plus compris la page de Gérard Villemin que ce que j'ai écrit.
À défaut de lire, Biname pourra peut-être comprendre un dessin d'avenue de longueur 3 ?
Pièce jointe 483422

Connaissant la vipère, j'ai lu deux fois avant de tirer

GBZM #207 "C'est clair, Biname ne sait pas lire."

GBZM #199
"Dans un pavage par dominos, les dominos sont des pâtés de maisons et les frontières entre les dominos des voies de circulation. Comme à New-York, une rue est une voie de circulation qui traverse en ligne droite le grillage de gauche à droite, et une avenue une voie de circulation qui traverse en ligne droite le grillage de bas en haut. Ce que Gérard Villemin appelle "pavage sans faute" est un pavage sans rue ni avenue."
GBZM #199 "SANSRUEAVE(7,8)"

Tu es enfermé dans le crible et ses indices. Lorsqu'on te demande d'écrire un élément d'un des ensembles qui entrent dans le crible, tu réponds , comennt veux tu trouver le miroir de ? C'est pour t'aider mon poussin que je te posais la question.

Concernant, les avenues verticales dans les espaces laisser libres par une route, c'est exactement le même problème que celui d'origine, seule la taille et l'orientation de la grille ont changé. Ma méthode utilisant la récurrence permet de calculer le nombre de cas pour chaque sans autres routes. Il suffit donc de ne pas compter les miroirs de .

GBZM : symétriques ? voir dessin Liet msg #137, ceux-là, je peux les retirer du compte.

if sym_list[i] == 0:
        tot_cases_no_mirror += cases

Pipeau ? Prouve-le ? C'est simple

Sejam

[GBZM]

Ça ne prouve rien du tout, parce que Miss Jenny a ajouté juste après :

je me suis mélangé les pinceaux avec les images, il y en a une en trop qui n'est pas bonne

Devine laquelle n'est pas bonne ? C'est effectivement celle que tu montres, puisqu'elle a deux avenues.
As-tu vraiment lu la page de Gérard Villemin que tu as mise en lien ?

[Biname]

C'est clair, Biname ne sait pas lire. Recopier in extenso un message que j'ai écrit, ce n'est pas lire (et ça ne sert à rien d'autre qu'à alourdir le fil).
Mais je ne suis loin d'être le seul objet de cette incompréhension : Biname n'a pas plus compris la page de Gérard Villemin que ce que j'ai écrit.
À défaut de lire, Biname pourra peut-être comprendre un dessin d'avenue de longueur 3 ?
Pièce jointe 483422

Mea Culpa ... erreur de ma part.
Avec, un petit dessin on comprend mieux, les rues et les blocs ... ! On change de sujet là, on 'fork' dans tous les sens aussi.
Le crible peut sortir les cas ?

Biname

[GBZM]

Oui Biname ne sait pas lire. Je le mets en gros ce qu'il a zappé :
les frontières entre les dominos des voies de circulation
Mais a-t-il compris le dessin ? A-t-il compris ce que sont les rues et avenues ?

Autre preuve qu'il ne sait pas lire : je n'ai pas répondu L_1, j'ai répondu en donnant UN ÉLÉMENT DE L_1 (dont il était facile de trouver le miroir : lui même).
J'ai répondu comme ça parce que Biname a été infoutu d'expliquer ce qu'il veut dire par "ensemble rentrant dans le crible".

Ensuite, Biname n'a pas compris le fonctionnement des mathématiques : quand on affirme quelque chose, il faut le prouver. Si on n'explique aucune idée et qu'on ne prouve rien, c'est bel et bien du pipeau.
En tout cas, les deux lignes de code données, c'est bel et bien du pipeau.
Je changerai d'avis quand Biname aura expliqué clairement son idée d'algorithme et que j'aurai vérifié que ça tient la route.

[Biname]

Oui Biname ne sait pas lire. Je le mets en gros ce qu'il a zappé :
les frontières entre les dominos des voies de circulation
Mais a-t-il compris le dessin ? A-t-il compris ce que sont les rues et avenues ?

Maintenant oui. Mes excuses !

Autre preuve qu'il ne sait pas lire : je n'ai pas répondu L_1, j'ai répondu en donnant UN ÉLÉMENT DE L_1 (dont il était facile de trouver le miroir : lui même).
J'ai répondu comme ça parce que Biname a été infoutu d'expliquer ce qu'il veut dire par "ensemble rentrant dans le crible".

Le crible calcule bien le cardinal de l'union d'un groupe d'ensembles ? Tu ne comprends pas ou tu ne veux pas comprendre ?

Ensuite, Biname n'a pas compris le fonctionnement des mathématiques : quand on affirme quelque chose, il faut le prouver. Si on n'explique aucune idée et qu'on ne prouve rien, c'est bel et bien du pipeau.

"T'es pas cap !" effet Pygmalion.
J'ai tout expliquer, va relire : récurrence, 2^L_i -1, binaire, miroir mais pour ça, il faut visualiser L_i

En tout cas, les deux lignes de code données, c'est bel et bien du pipeau.
Je changerai d'avis quand Biname aura expliqué clairement son idée d'algorithme et que j'aurai vérifié que ça tient la route.

J'ai tout expliqué, mais tu t'y es autant intéressé que je me suis intéressé au crible, voire moins encore. Tu as 216 messages à lire.
Biname

[GBZM]

Le crible calcule bien le cardinal de l'union d'un groupe d'ensembles ? Tu ne comprends pas ou tu ne veux pas comprendre ?

Oui, il était ici employé à calculer le cardinal de la réunion des L_i, où j'ai défini L_i comme étant l'ensemble des pavages présentant un chemin traversant horizontal en ligne n°i. Donc j'ai répondu

Que veut dire "un ensemble qui entre dans le crible pour L7 et C8 " ?
Tu veux parler par exemple de l'ensemble des pavages qui ont un chemin traversant de dominos horizontaux en ligne n° 4 ?
Facile : le pavage où tous les dominos sont horizontaux.

J'ai donné un élément d'un "ensemble qui entre dans le crible", donc Biname a sa réponse et il est content.

J'ai tout expliqué

C'est faux, Biname n'a rien expliqué en ce qui concerne le miroir. J'ai bien suivi et compris l'idée de ce qu'il faisait en comptant les pavages sans chemin traversant et qu'il a pu laborieusement mettre au point en s'aidant des résultats obtenus les doigts dans le nez par la méthode du crible de Poincaré. Mais pour le miroir, je n'ai rien vu qui tienne la route. Rien, nada.
Je ne sais pas calculer le nombre de pavages par dominos d'une grille m x n à symétrie près (on ne s'occupe même pas de l'existence ou non d'un chemin traversant), et ça ne me semble pas simple comme problème. Je n'ai vu dans les messages de Biname aucune idée susceptible de résoudre ce problème.

[Liet Kynes]

Ça ne prouve rien du tout, parce que Miss Jenny a ajouté juste après :

Devine laquelle n'est pas bonne ? C'est effectivement celle que tu montres, puisqu'elle a deux avenues.
As-tu vraiment lu la page de Gérard Villemin que tu as mise en lien ?

Ben oui et j'ai considéré celle avec avenues (ligne verticale de la grille) comme étant la bonne (la "pas-surnuméraire") justement car elle apporte une information que l'autre ne donne pas à savoir que ce n'est pas les lignes de la grille traversantes mais les allignements de dominos que l'on cherche.
Si l'on conserve l'autre l'ambiguïté demeure, de plus MissJenny nous aurait signalé la méprise.

[Biname]

Oui, il était ici employé à calculer le cardinal de la réunion des L_i, où j'ai défini L_i comme étant l'ensemble des pavages présentant un chemin traversant horizontal en ligne n°i. Donc j'ai répondu

J'ai donné un élément d'un "ensemble qui entre dans le crible", donc Biname a sa réponse et il est content.

C'est faux, Biname n'a rien expliqué en ce qui concerne le miroir. J'ai bien suivi et compris l'idée de ce qu'il faisait en comptant les pavages sans chemin traversant et qu'il a pu laborieusement mettre au point en s'aidant des résultats obtenus les doigts dans le nez par la méthode du crible de Poincaré. Mais pour le miroir, je n'ai rien vu qui tienne la route. Rien, nada.
Je ne sais pas calculer le nombre de pavages par dominos d'une grille m x n à symétrie près (on ne s'occupe même pas de l'existence ou non d'un chemin traversant), et ça ne me semble pas simple comme problème. Je n'ai vu dans les messages de Biname aucune idée susceptible de résoudre ce problème.

Je crois que tu n'as pas VU ce que tu calcules avec le crible.

Si tu croyais vraiment que j'affabule, tu ne me répondrais pas . M'étant un peu intéressé au crible, il me __semble__ que j'y ai vu les symétries/miroirs dont on parle, il suffirait peut-être les 'effacer/enlever' avant de passer à PI : affiche la liste C de ton code SageMath, j'ai posté ici une capture d'écran commentée de cette liste msg ???.

Tu pourras alors prouver que je me suis trompé, j'ai donné ma clé

Biname

[GBZM]

Que ce soit avec la formule d'inclusion-exclusion ou avec les bricolages de Biname, ce qui intervient est la position des chemins traversants horizontaux, et rien d'autre. On peut certes se limiter aux positions symétriques pour ces chemins traversants horizontaux. Mais ça ne fait pas pour autant des pavages symétriques. Si on a un chemin traversant horizontal en position mediane (avec 3 lignes au-dessus et 3 lignes au-dessous), ça va. Mais sinon, on n'y coupe pas, il faut savoir compter le nombre de pavages par dominos symétriques. Et ça, Biname n'a aucune idée pour le faire. C'est normal, je n'en ai pas non plus, ça me semble difficile. Le problème avec Biname, c'est qu'il croit savoir faire.
Je lui ai demandé plusieurs fois comment compter le nombre de pavages par dominos symétriques (ou compter le nombre de pavages par dominos modulo symétrie) pour une grille m x n, sans rien demander au pavage d'autre que d'être un pavage par dominos. Bien sûr, pas de réponse.

[Liet Kynes]

Que ce soit avec la formule d'inclusion-exclusion ou avec les bricolages de Biname, ce qui intervient est la position des chemins traversants horizontaux, et rien d'autre. On peut certes se limiter aux positions symétriques pour ces chemins traversants horizontaux. Mais ça ne fait pas pour autant des pavages symétriques. Si on a un chemin traversant horizontal en position mediane (avec 3 lignes au-dessus et 3 lignes au-dessous), ça va. Mais sinon, on n'y coupe pas, il faut savoir compter le nombre de pavages par dominos symétriques. Et ça, Biname n'a aucune idée pour le faire. C'est normal, je n'en ai pas non plus, ça me semble difficile. Le problème avec Biname, c'est qu'il croit savoir faire.
Je lui ai demandé plusieurs fois comment compter le nombre de pavages par dominos symétriques (ou compter le nombre de pavages par dominos modulo symétrie) pour une grille m x n, sans rien demander au pavage d'autre que d'être un pavage par dominos. Bien sûr, pas de réponse.

J'en suis au même point que toi dans le raisonnement, je cherche une relation éventuelle entre le ratio "symétriques traversants"/"traversants non symétriques" et "symétriques non traversants"/"non traversants non symétriques" sachant que ce qui est en bleu on ne sais pas le calculer, je cherche à partir de grilles plus petites et je compte "à la main"

[Biname]

Que ce soit avec la formule d'inclusion-exclusion ou avec les bricolages de Biname, ce qui intervient est la position des chemins traversants horizontaux, et rien d'autre. On peut certes se limiter aux positions symétriques pour ces chemins traversants horizontaux. Mais ça ne fait pas pour autant des pavages symétriques. Si on a un chemin traversant horizontal en position mediane (avec 3 lignes au-dessus et 3 lignes au-dessous), ça va. Mais sinon, on n'y coupe pas, il faut savoir compter le nombre de pavages par dominos symétriques. Et ça, Biname n'a aucune idée pour le faire. C'est normal, je n'en ai pas non plus, ça me semble difficile. Le problème avec Biname, c'est qu'il croit savoir faire.
Je lui ai demandé plusieurs fois comment compter le nombre de pavages par dominos symétriques (ou compter le nombre de pavages par dominos modulo symétrie) pour une grille m x n, sans rien demander au pavage d'autre que d'être un pavage par dominos. Bien sûr, pas de réponse.

Je sais distinguer, compter ou pas, chacun de ces cas là (Liet msg #137) :

mon infâme bricolage, faut appeler les choses par leur nom(je sens que tu te retiens) donne le nombre de cas pour chacune des 'combinaisons' possibles de routes.

Je remarque en lisant ton texte que tu as progressé.

D'autres clés, tu finiras par trouver et qui d'autres que toi viendra vérifier ? Je finirai aussi par lâcher le morceau , tout est prêt.

 Cliquez pour afficher

--------------------------------------------------------------------------------------------------------------- 
L=17, C=18

                              Total des cas avec au moins une route :     60849582608756030485054863767664589
           Total des cas avec au moins une route sans les miroirs H :     31421480037511218205974731970734430

Temps de calcul : 4332.98 ms
Temps de  print : 455.26 ms
Temps     total : 4788.23 ms
--------------------------------------------------------------------------------------------------------------- 
L=18, C=19
		          Total des cas avec au moins une route :     1210382424042842325920437697315243476083
        Total des cas avec au moins une route sans les miroirs H :     606198517975221257605586577323225946875

Temps de calcul : 9171.57 ms
Temps de  print : 985.68 ms
Temps     total : 10157.25 ms
---------------------------------------------------------------------------------------------------------------
L=19, C=20
                        Total des cas avec au moins une route :     42033575612041018992520708390570225656482917
     Total des cas avec au moins une route sans les miroirs H :     21227964547507591620295788172646969223751753

Temps de calcul : 19540.21 ms
Temps de  print : 2006.74 ms
Temps     total : 21546.96 ms
---------------------------------------------------------------------------------------------------------------

Biname

[GBZM]

Ce que Biname ne comprend toujours pas, c'est que la difficulté est de distinguer entre le cas de gauche (symétrique) et le cas de droite (asymétrique) ici :

[Liet Kynes]

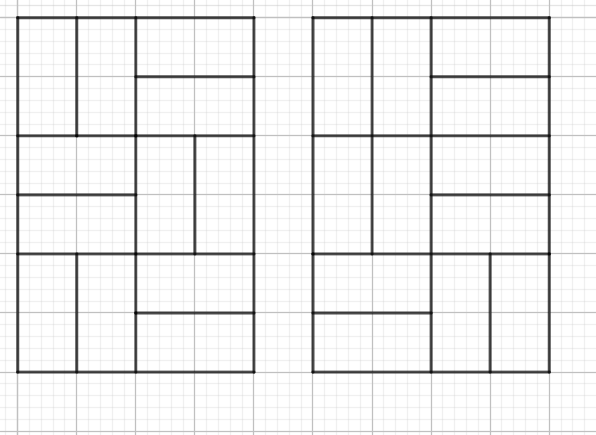
Ce que l'on peut compter c'est les symétriques traversants et déduire les doublons de l'ensemble de tous les pavages.
Ce que l'on ne sais pas encore compter c'est les symétriques non traversants : il faut déduire aussi ces doublons de l'ensemble de tous les pavages.

[GBZM]

Hum ... Tu fais la différence entre le traversant de gauche (symétrique) et celui de droite (asymétrique) ?

Les deux ont le même code 10000001

[Liet Kynes]

Euh ce n'est pas ce genre de symétrie dont on parle, le terme est d'ailleurs mal choisi cf##210

[Biname]

Ce que l'on peut compter c'est les symétriques traversants et déduire les doublons de l'ensemble de tous les pavages.
Ce que l'on ne sais pas encore compter c'est les symétriques non traversants : il faut déduire aussi ces doublons de l'ensemble de tous les pavages.

Oui, ton fichier excel peut aussi facilement exclure les miroirs H, il suffit de ne pas multiplier par deux, il te reste à automatiser la recherche des 'miroirs H'. Et GZBM nous répond symétriques.
xxxx ad hominem xxxx

Biname

[Biname]

Hum ... Tu fais la différence entre le traversant de gauche (symétrique) et celui de droite (asymétrique) ?

 Cliquez pour afficher

Pièce jointe 483457

Les deux ont le même code 10000001

Non ! Explique . celui de gauche est aussi un mirror_H, ta symétrie est X( ! aux jacobiens).
Si tu précisais l'axe de la symétrie, tu nous aiderais.
Biname

[GBZM]

Dans mon exemple précédent, le pavage de gauche a un axe de symétrie horizontal, celui de droite n'a aucune symétrie. Les deux partagent le code 10000001.

Un nouvel exemple, toujours avec le code 10000001 :

Le pavage de gauche a toutes les symétries du rectangle : axe horizontal, axe vertical, rotation d'un demi-tour. Celui de droite n'a aucune symétrie.
Si Biname pouvait utiliser un peu moins d'insultes et un peu plus d'arguments, le fil aurait une meilleure tenue.

[Liet Kynes]

Dans mon exemple précédent, le pavage de gauche a un axe de symétrie horizontal, celui de droite n'a aucune symétrie. Les deux partagent le code 10000001.

Un nouvel exemple, toujours avec le code 10000001 :

Le pavage de gauche a toutes les symétries du rectangle : axe horizontal, axe vertical, rotation d'un demi-tour. Celui de droite n'a aucune symétrie.
Si Biname pouvait utiliser un peu moins d'insultes et un peu plus d'arguments, le fil aurait une meilleure tenue.

Ah oui, je vois le problème, donc c'est plus grave que ce que l'on peut croire.. cela devient impossible

[GBZM]

Impossible, peut-être pas. Mais nécessitant d'autres idées que celles qu'on a pu rencontrer dans ce fil, sûrement.
Si je voulais sérieusement m'investir dans ce sujet, je commencerais par bien étudier la façon d'aboutir à la formule de comptege des pavages par dominos.

[Liet Kynes]

Après, il y a l'idée de se dire que tout pavage possède 0, 1 ou 3 miroirs. Le nombre de "0 miroirs" étant le plus facile à déterminer, déterminer le nombre à "deux miroirs" permet de déduire celui à "3".

Les pavages à "0 miroirs" de la grille 7*8, j'en trouve 15, en ai-je oublié ? :

[Merlin95]

En passant, on peut aussi dire je crois qu'il y a moins de combinaisons, mais c'est une approximation grossière car elle compte plusieurs fois les configurations symétriques et parcequ'elle se base sur un nombre de jetons grossièrement majoré.

[GBZM]

@Liet : puisqu'il y a 11 pavages par dominos d'un rectangle 3 x 4, il y en a déjà deux qui manquent dans ta liste construits à partir d'un tel rectangle pavé et d'une ligne médiane de dominos horizontaux, en utilisant les symétries.
À mon avis il en manque pas mal d'autres

[GBZM]

En fait, il ne t'en manque pas tant que ça puisqu'il y en a 19 en tout, sauf erreur. Les 11 du type mentionnés ci-dessus (il t'en manque 2), et 8 autres (il t'en manque aussi 2).

[Liet Kynes]

Version complétée :

[MissJenny]

je ne pensais pas que ma question susciterait tant d'intérêt... elle était hélas mal posée et je pensais effectivement aux espaces entre les dominos, comme l'a compris GBZM. Mais l'autre question est intéressante elle aussi ... et on peut en imaginer d'autres, tiens avec des "dominos" tridimensionnels (pour les courageux).

[Liet Kynes]

je ne pensais pas que ma question susciterait tant d'intérêt... elle était hélas mal posée et je pensais effectivement aux espaces entre les dominos, comme l'a compris GBZM. Mais l'autre question est intéressante elle aussi ... et on peut en imaginer d'autres, tiens avec des "dominos" tridimensionnels (pour les courageux).

Ok, ton dernier message ne laissait pas présager une telle évolution du fil,

merci pour vos réponses.

Quand on joue au jeu dominosa, les configurations sans "chemin traversant" sont rares, ce qui, d'après les calculs de GBZM, laisse penser que les configurations ne sont pas tirées au hasard uniformément parmi toutes les configurations possibles. Ca peut être dû à l'algorithme utilisé, mais c'est sans-doute aussi parce que dans le jeu dominosa il y a une contrainte supplémentaire : la solution doit être unique. Or le cas le plus simple de non-unicité est la situation où deux dominos forment un carré de 2x2 cases dont la diagonale porte un chiffre commun. Donc je soupçonne que les configurations choisies pour le jeu comportent relativement peu de carrés 2x2. (mais la question posée ne parlait pas ce ça).

On peut facilement en conclure que le pavage de dominos c'est de la géométrie variable.

[GBZM]

Oui, Liet Kynes, tu as les 19. On voit bien que compter les symétriques n'est pas simple. Je ne pense pas que Biname soit plus avancé que nous, il nous dira peut-être ...
La version du problème à laquelle pensait Miss Jenny est aussi résolue : mon message # 199 ; il y a seulement 13 514 pavages "sans faute" (c.-à-d. sans rue ni avenue) sur les 1 292 697, soit à peine un peu plus de 1%.