Bonjour Messieurs,
Je vous propose d'étudier la variante suivante:
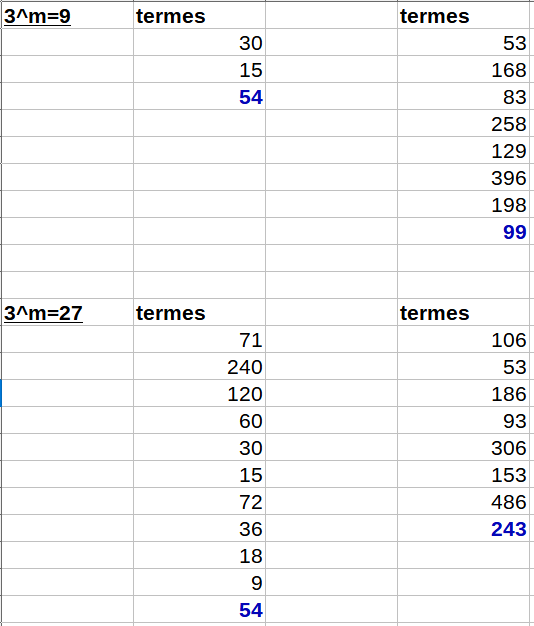
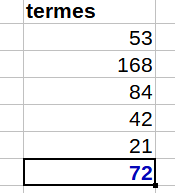
Pouron retrouve Syracuse.
Il me semble que Si
Lorsque
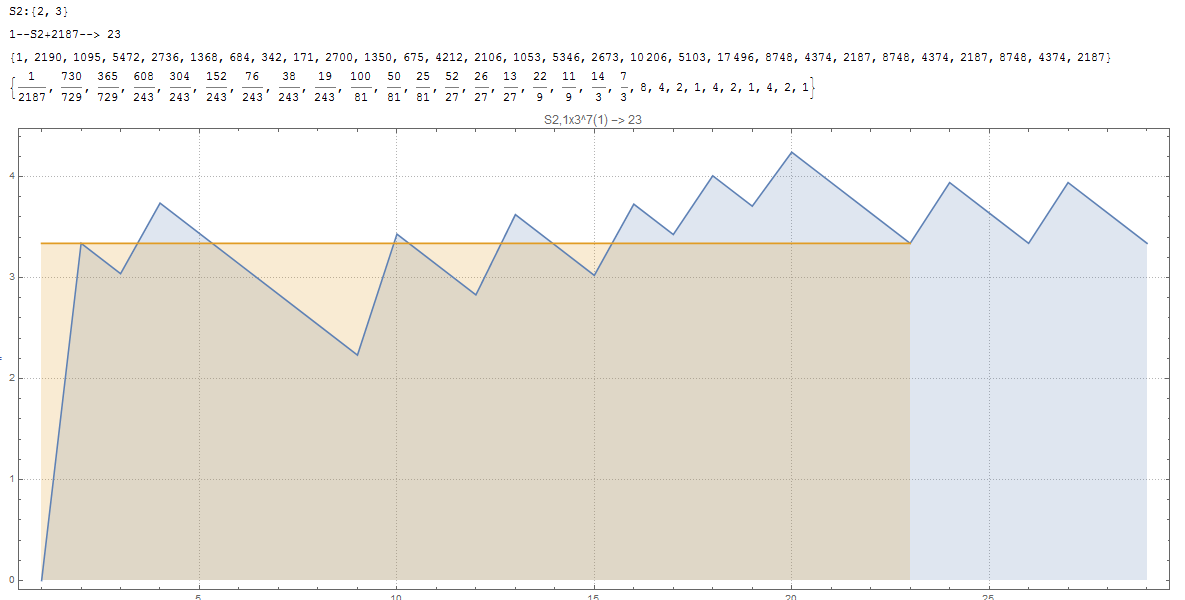
Pour les autres nombres il n'est pas évident du tout de comprendre pourquoi on finira sur le cycle trivial.
Et pourtant des tests numériques montrent que
Merci de bien vouloir commenter.
Bonjour et bienvenue sur le forum,
Le forum est mixte.Envoyé par lby2lby2
Cette phrase laisse supposez que vous l'avez démontré. Peut-on voir cette démonstration ? ("il me semble que" n'en n'est pas une).
Rappel : Cela n'est pas une preuve, quand bien même cela serait vrai jusqu'à un gogolplex.Et pourtant des tests numériques montrent que
Quel est l'intérêt de votre variante ?
Not only is it not right, it's not even wrong!
Bonjour albanxii,
Merci pour votre réponse P.V.
Le forum est mixte.
Certes mais si je ne souhaite m'adresser qu'aux hommes car les femmes m'intimident (Et pourtant les femmes sont des Hommes comme les autres. Il ne s'agirait donc que d'une peur mal motivée).
Rappel : Cela n'est pas une preuve, quand bien même cela serait vrai jusqu'à un gogolplex.
Dans mon message il n'est nul part question de théorème ni de preuve. Il est même clairement notifié qu'il s'agit de calculs numériques dans des bornes indiquées.
Il s'agit donc uniquement d'un indice pour encourager ceux qui auraient l'outrecuidance de penser avoir le niveau en théorie des nombres a se lancer à la poursuite d'une démonstration.
Quel est l'intérêt de votre variante ?.
Il s'agit simplement d'une restriction de la conjecture
Voir :
Primitive Cycles Existence Conjecture (Lagarias (1990)
Finite Primitive Cycles Conjecture (Lagarias (1990)
Belaga & Mignotte (2006)
(3x + d)-Cycle Conjecture (Kaneda, 2014)
Pour ne citer qu'eux.
A la lecture de ces différentes sources, j'ai constaté que d'aucun n'avait signalé la propriétés que j'énonce (Conjecture bien sûr).
En espérant que ce bel après midi vous ait occasionné d'agréables loisirs,
Salutations.
Tu peux développer cela? j'ai mal compris.
Lorsque
.
Sans questions il n'y a que des problèmes sans réponses.
Oui bien sûr!
Syracuse: 3N+1 finit toujours par le cycle 1,4,2,1
Pour m>0,
3N+3 finit toujours par le cycle 3,12,6,3
3N+9 finit toujours par le cycle 9,36,18,9
3N+27 finit toujours par le cycle 27,108,54,27
...
3N+3^m finit toujours par le cycle 3^m,4*3^m,2*3^m,3^m,
Est-ce une constatation ou as-tu une preuve ? Tu redis l'affirmation, sans justifier le "homothétique".
Cordialement.
to gg0,
Comme indiqué dans le message initial (relire) il s'agit d'un test numérique sur de large plages.
to gg0,
la série est homothétique d'une série de Syracuse
Si N= k*3^m
La suite de Syracuse de k sera {k,k1,k2,k3,...,1,4,2,...}
La suite de Syracuse(3^m) de N sera {k*3^m,k1*3^m,k2*3^m,k3*3^m,.. .,1*3^m,4*3^m,2*3^m,...}
Dans ce cas simple les S(N) est homothétique de S(k) d'un facteur 3^m
car si ki est pair alors ki*3^m est pair et si ki est impair alors ki*3^m est impair.
En dehors de ce cas particulier, la série de N ne pourra être ramenée à une série Syracuse par aucune homothétie.
Bonjour,
Oui c'est ce que j'allais écrire : par "la série est homothétique d'une série de Syracuse" vous voulez dire que si
Pour les autres nombres, je crois qu'on peut expliquer (sinon démontrer) assez facilement la propriété que vous avez trouvée.
Prenons un nombre N qui n'est pas congru à 0 modulo
Maintenant notons
Alors :
- quand on applique l'étape "N pair" la valeur de
- quand on applique l'étape "N impair" i augmente de 1 puisqu'on multiplie par
.... ainsi de suite jusqu'à ce que
Dernière modification par Juzo ; 17/06/2024 à 16h34.
Les fleurs du cerisier rêvent en blanc les fruits qu'elles ne voient pas.
EDIT : il y a une erreur sur l'étape "N pair" que je vais regarder de plus près, le raisonnement de l'étape "N impair" me paraît ok.
Les fleurs du cerisier rêvent en blanc les fruits qu'elles ne voient pas.
En fait je crois que je me suis compliqué la tache pour rien, si
Je résume la démonstration simplifiée.
Soit N un entier non congru à 0 modulo
Soit
- Si N est pair :
Donc
- Si N est impair :
On voit à la fin de la dernière expression que l'itération de ces étapes va mener à l'augmentation de l'indice
Les fleurs du cerisier rêvent en blanc les fruits qu'elles ne voient pas.
To Juzo,
Bien vu!
Salut Juzo,
Maintenant notons i le plus grand entier tel que C=3^i . On a i<m .
Souvent aucune valeur de i ne satisfait la condition.
Exemple : N=29, m=3 => C=2 , aucune valeur de i tel que C=3^i
La suite de votre travail part sur de mauvaises bases me semble-t-il?
à suivre...
Bonjour,
Oui il y a bien i=0 car C est congru à 0 modulo 1.
Attention je parle de congruence, pas d'être égal à 3^i.
Ainsi 2 est congru à 0 modulo 1.
Dernière modification par Juzo ; 18/06/2024 à 10h05.
Les fleurs du cerisier rêvent en blanc les fruits qu'elles ne voient pas.
To Juzo
Tout nombre est congru à 0 modulo 1 et cela n'apporte rien.
Je suis en mesure de montrer (un peu d'arithmétique modulaire) que si N n'est pas multiple de 3^m, les opérations: division par 2 quand c'est possible et multiplication par 3 puis ajout de 3^m sinon, ne donneont jamais un multiple de 3^m
Ben oui ça apporte qu'on peut démontrer la propriété voulue pour tout nombre, et ce n'est pas rien.
Ce serait étonnant car ça marche sur les 4 exemples au hasard que j'ai pris (les nombres obtenus en bleu sont des multiples de 3^m).
Les fleurs du cerisier rêvent en blanc les fruits qu'elles ne voient pas.
Les termes corrects de la suite en haut à droite qui commence à 53 sont :
Les fleurs du cerisier rêvent en blanc les fruits qu'elles ne voient pas.
To Juzo
La série 53 est fausse 53,168,84,... (pas grave)
Les autres sont correctes et c'est justement ce dit l'extension de la conjecture (atterrissage sur 3^m).
Ma phrase "Je suis en mesure de montrer (un peu d'arithmétique modulaire) que si N n'est pas multiple de 3^m, les opérations: division par 2 quand c'est possible et multiplication par 3 puis ajout de 3^m sinon, ne donneront jamais un multiple de 3^m" est évidement fausse, contredirait la conjecture et ce n'est pas du tout ce que je suis en train de démonter actuellement (Réponse trop rapide et non réfléchie, désolé!).
Vous dites "On voit à la fin de la dernière expression que l'itération de ces étapes va mener à l'augmentation de l'indice i jusqu'à i=m et on retombe sur la suite homothétique."
Il me semble que vous ayez juste.
Mes tests montrent effectivement une convergence progressive (à chaque fois que N est impair) vers un multiple de 3^m.
{S2,+27,0(106)}/27={106/27,53/27,62/9,31/9,34/3,17/3,18,9,28,14,7,22,11,34,17,52,2 6,13,40,20,10,5,16,8,4,2,1,4,2 ,1,4,2,1}
Je montre la série divisée par 3^m qui me semblent plus explicites.<br>
Un autre exemple:
Auriez-vous l'amabilité de mettre en forme l'énoncé et la démonstration afin d'avoir une conclusion nette.
YLB alias lby2lby2.
Oui j'ai corrigé au message #18.
Je suis désolé mais je ne vais pas pouvoir détailler la rédaction de l'énoncé qui prendrait beaucoup de temps.
Il faudrait noter Tn la suite où l'on ajoute 3^n au lieu de 1 lorsque N impair par rapport à la suite de Syracuse, puis définir Tn exactement de la même manière qu'on définit la suite de Syracuse.
Pour le reste il faut rédiger rigoureusement le cas N = k*3^n : on a 3^n fois la suite de Syracuse appliquée à k.
Ensuite la rédaction du message #12 me paraît assez complète (il faut préciser par exemple que k et C appartiennent à
Reste à revoir la dernière phrase "On voit à la fin de la dernière expression que l'itération de ces étapes va mener à l'augmentation de l'indice i jusqu'à i = m", mais je ne sais pas comment la formuler plus rigoureusement.
Par exemple : le nombre d'étapes "N pair" successives est nécessairement fini, donc en faisant un nombre d'étapes assez grand on appliquera nécessairement j fois l'étape "N impair". L'indice i vaudra i+j=m. La congruence du terme de la suite modulo 3^m sera donc elle-même congrue à 0 modulo 3^m, ce qui permet de conclure que le terme sera congru à 0 modulo 3^m.
Il ne reste plus qu'à "recoller" tous les morceaux, ça serait très long en Latex. Précisons que je ne suis pas totalement à l'aise avec l'étape "N pair" (même si je pense que ça se tient).
Les fleurs du cerisier rêvent en blanc les fruits qu'elles ne voient pas.
To Juzo réponse à #20
Merci pour cette aide précieuse.
Je tiendrais compte de ces remarques pour tenter une rédaction que je mettrai sur le site mentionné plus bas.
Reste à revoir la dernière phrase "On voit à la fin de la dernière expression que l'itération de ces étapes va mener à l'augmentation de l'indice i jusqu'à i = m", mais je ne sais pas comment la formuler plus rigoureusement.
Par exemple : le nombre d'étapes "N pair" successives est nécessairement fini, donc en faisant un nombre d'étapes assez grand on appliquera nécessairement j fois l'étape "N impair". L'indice i vaudra i+j=m. La congruence du terme de la suite modulo 3^m sera donc elle-même congrue à 0 modulo 3^m, ce qui permet de conclure que le terme sera congru à 0 modulo 3^m.
C'est parfait.
Lorsque l'on a rejoint un multiple de 3^m on se retrouve dans une suite classique de Syracuse multiplié par 3^m. Pour l'instant (conjecture oblige) rien ne prouve qu'on atterrira sur 3^m.
Si j’appelle la suite S2,+1,m(N) c'est que j'explore des extensions plus importantes de la forme Sn,+M,m(N)
Sur la page internet http://www.arpege-expertise.com/syra...efinition.html (en préparation) je présente cet ensemble beaucoup plus vaste de conjectures.
Bonjour,
Je ne connais pas trop les théories du chaos mais on serait tenté de parler de chaos et d'attracteur(s) pour décrire le comportement de ces suites, non ?
Les fleurs du cerisier rêvent en blanc les fruits qu'elles ne voient pas.
Salut Juzo,
Je suis pas sur que l'on puisse parler de chaos. Les théories du chaos sont sur des nombres réels ou complexes, pas sur les entiers.
Par ailleurs ces suites (sauf divergence) finissent toujours sur un cycle (parfois très long), et d'autre part la répartition sur les différents cycles est très organisée.
J'ai déjà lu des papiers faisant l'étude de 3x+d sur les nombres réels et complexes, peut être dans ce cadre on pourrait parler de chaos et d'attracteurs.
Par ailleurs ailleurs j'ai commencé la rédaction de ta brillante démonstration sur les suites 3N+3^m.
Je galère avec LaTex (Brrr..) et ai du mal à décrire aussi bien les hypothèses que les démonstrations car je n'ai jamais rédigé de papier mathématique.
A+
To Juzo
Bonjour et re-Bonjour,
CaptYann-1.PNG
Yann-1.pdf
J'ai essayé de faire une rédaction.
Merci de bien vouloir en faire une critique constructive.
Yann Le Bihan
Bonjour,
Je n'ai pas d'ordinateur avec moi donc je ne vais pas pouvoir faire de commentaire détaillé de la rédaction.
La 2ème phrase peut être simplifiée en "on note.... le terme de rang i de la suite". J'aurais plutôt tendance à le noter
Il y a un problème avec le modulo 3^i, il faut mettre le 3^i entre accolades.
Il faut éviter de mélanger des explications avec la démonstration, la démonstration doit être purement formelle.
Cest vrai qu'il est plus simple comme vous le proposez de regarder directement la congruence de
Effectivement on va avoir un gros problème pour utiliser la théorie du chaos avec un espace des états qui est discret. Néanmoins la suite comporte des caractéristiques du chaos : sensibilité aux conditions initiales, évolution pseudo-aléatoire. On remarque aussi que la manière dont on itère les termes favorise les oscillations. Néanmoins tout suite semble finir sur un cycle.Je suis pas sur que l'on puisse parler de chaos
Je crois qu'on peut sans trop de risque parler de "comportement pseudo-chaotique transitoire".
Il pourrait être utile d'utiliser certain vocabulaire de théorie du chaos (orbite, point périodique, attracteur).
Il serait intéressant par ailleurs de chercher comment la définition mathématique d'un système chaotique peut être adaptée sur un système dont l'espace des états est discret, mais plutôt en Science ludique. Et je suis peut-être hors sujet !
Les fleurs du cerisier rêvent en blanc les fruits qu'elles ne voient pas.
Je corrige le mod 3^i que je n'avais pas vu.
J'ai trouvé aussi in "itration".
"Il faut éviter de mélanger des explications avec la démonstration, la démonstration doit être purement formelle."
Qu'est ce à dire? Je ne vois pas bien comment modifier.
Précise moi quand tu aura un moment, STP.
Yann.pdf
Le chaos en espace discret, difficile à définir, non?
Dans S9,+M,0 j'ai trouvé des suites de plus d'un million d'éléments avant cycles avec un cycle de plus de 60 000 éléments.
Des comportements étranges mais qui finissent toujours par un cycle (Dans les limites du calculables. sur ces monstres je n'ai pas calculé pour N>1 000 000 000.).
Je pensais aux phrases en italiques avec du langage naturel comme "Une ou plusieurs valeurs de i existent. Prenons..." ou "N est pair, on devra donc le diviser par 2", etc.Qu'est ce à dire? Je ne vois pas bien comment modifier.
Précise moi quand tu aura un moment, STP.
Je ne sais pas, mais rien ne s'oppose à ce qu'une suite "sensible" aux conditions initiales et au développement pseudo-aléatoire puisse exister en espace discret. Évidemment le chaos mathématiquement ce n'est pas que ça, mais c'est l'idée principale.Le chaos en espace discret, difficile à définir, non?
Les fleurs du cerisier rêvent en blanc les fruits qu'elles ne voient pas.
Bonsoir albanxiii,
Je voudrais savoir si un utilisateur peux modifier ou effacer une réponse qu'il a faite. Et si Oui de quelle façon.
Dans cette discussion ma réponse #22 n'a rien à faire là et je souhaiterais en faire une nouvelle discussion.
Merci de bien vouloir m'apporter votre précieuse aide technique.
Syracuse sur
Pour z entier on a z/2 si z pair et 3z+1 si z impair.
On peut en faire une fractal:
Ici une Julia ou z0=0.005+0.505 î
Serait-on dans Chaos?
Bonjour,
C'est astucieux la formule avec les cosinus.
Quelques éléments du livre "Chaos et déterminisme", de 1990 dont j'ai commencé la lecture :
On pourra parler de système dynamique, le nombre d'itérations correspondant à un temps (discrétisé) dans le cas d'une suite. On pourrait définir deux comportements "extrêmes" quand on étudie les systèmes dynamique : le comportement pseudo-périodique et le comportement hyperbolique.
Beaucoup d'applications se trouvent dans un intermédiaire entre ces deux comportements, qu'on a du mal à définir mathématiquement.
Les comportements pseudo-périodiques sont plutôt anecdotiques sur l'ensemble des applications, mais deviennent plus fréquents jusqu'à être non négligeables quand on étudie spécifiquement les applications conservatives, c'est-à-dire qui conservent les aires.
A partir de là, quelques spéculations :
- Les suites chaotiques connues (suites logistique, suite de Héron, suite de Ricker, suite de Verlhust, doublement du cercle...) semblent toujours comporter dans leur définition par récurrence une partie qui favorise le comportement pseudo-périodique et une partie favorisant un comportement hyperbolique qui amplifie l'erreur. Je pensais peut-être faire un fil plus détaillé là-dessus.
Un exemple très connu : la suite logistique
L'amplification de l'erreur se fait par la multiplication de celle-ci par 4 et par un terme de l'ordre de
Le comportement pseudo périodique est obtenu par la multiplication de
Un exemple connu et très élégant : la suite du doublement du cercle. On définit un angle
Cela revient à doubler un nombre modulo 1 à chaque itération.
L'amplification de l'erreur est obtenue par le facteur 2.
Le comportement pseudo-périodique vient du modulo 1.
- Concernant notre suite (la suite de Syracuse) on retrouve bien ces deux éléments (ce qui motivait que je parle de pseudo-chaos, pour l'augmentation de l'erreur je ne suis pas sûr néanmoins) :
La multiplication par 3 dans le cas impair et division par 2 dans le cas pair augmente l'erreur (cela revient à la multiplier par 3/2 en moyenne s'il y a autant de pairs que d'impairs dans la suite)
Le fait de diviser un nombre pair jusqu'à tomber sur un impair puis multiplier le nombre impair qui donne à nouveau un pair crée le comportement pseudo-périodique.
Hélas la comparaison a des limites.
Le puits qui est le cycle 4 - 2 - 1 dans lequel on tombe à partir de n'importe quelle puissance de 2 fait que l'application n'est pas conservative, donc (pas sûr de ce donc) le comportement pseudo-périodique n'est que transitoire. (est-ce que cela empêche aussi le mélange topologique ?)
Le fait que l'espace est discrétisé fait qu'on peut oublier les notions de sensibilité aux conditions initiales (pour un erreur arbitrairement petite on pourra obtenir un écart arbitrairement grand des valeurs de la suite au bout d'un temps suffisant), de densité des points périodique etc.
Néanmoins on pourrait envisager de montrer que la suite de Syracuse est un cas particulier d'une suite chaotique.
Par exemple la suite qui serait définie ainsi :
- Si l'arrondi de
- Si l'arrondi de
Hélas aussi, ce serait bien que toute suite extraite d'une suite chaotique soit chaotique, mais je crois que ce n'est pas le cas (en tout cas selon ChatGPT).
Désolé c'est un peu long mais il y a 1h ou 2 de "travail" derrière.
Référence du livre "Déterminisme et chaos" qu'au passage je trouve passionnant : https://www.gibert.com/chaos-et-dete...e-4178864.html. Est-ce que quelqu'un l'aurait lu et aurait un avis sur ce livre ?
Bonne journée
Les fleurs du cerisier rêvent en blanc les fruits qu'elles ne voient pas.
