Suite relativité

[coussin]

Il y a des lecteurs silencieux qui pourraient être intéressé.
m@ch3

OK.
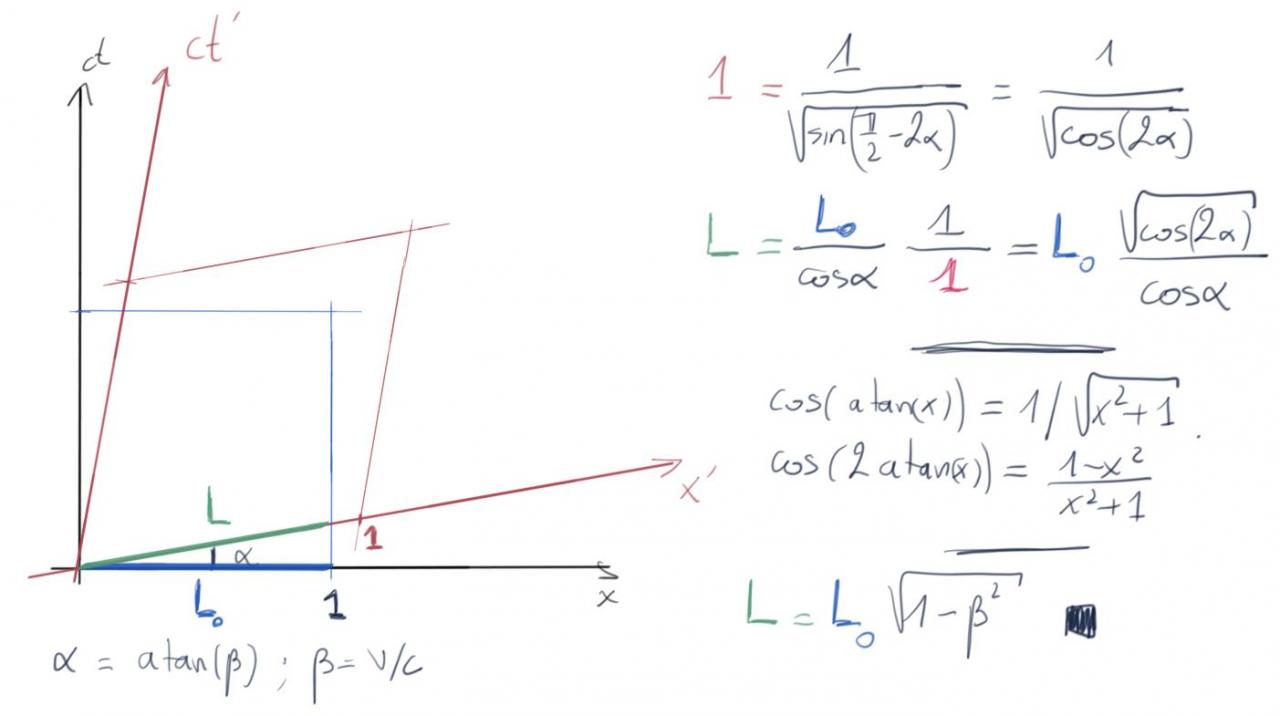
Je considère un repère (x,ct) noir et (x',ct') en rouge. Un barreau immobile dans (x,ct), de longueur propre L0 dans ce référentiel. La longueur de ce barreau dans (x',ct') est la longueur L, représentée en vert. Les axes (x') et (ct') se ferment comme les lames d'un ciseau d'un angle alpha=atan(v/c).
La petite particularité est que l'unité de longueur le long de l'axe x (le "1" noir) est différent de l'unité de longueur le long de l'axe x' (le "1" rouge). Plusieurs méthodes existent pour savoir où mettre le "1" rouge; celle que je préfère est basée sur le fait que les transformations de Lorentz conservent les surface dans un tel diagramme de Minkowski. Cela signifie que l'aire du carré bleu doit être égale à l'aire du losange rouge. D'après la formule de l'aire d'un losange, on trouve la première relation.
On obtient la deuxième expression en utilisant la définition du cosinus dans le triangle rectangle d'angle alpha et de côtés L et L0, sans oublier la redéfinition de l'unité de longueur le long de (x').
Il existe des identités trigonométriques pour le cos d'un atan et on arrive au résultat escompté.


-----

[Sethy]

La petite particularité est que l'unité de longueur le long de l'axe x (le "1" noir) est différent de l'unité de longueur le long de l'axe x' (le "1" rouge).

Tout d'abord, merci pour ce développement.

Juste une précision. Je suppose que l'aire du carré bleue est mesurée dans le repère bleu et que l'aire du losange rouge est mesurée dans le repère rouge (çàd avec la norme rouge) ?

[Deedee81]

Sous-discussion issue de https://forums.futura-sciences.com/p...elativite.html
A la demande de Sethy.

[mach3]

Juste une précision. Je suppose que l'aire du carré bleue est mesurée dans le repère bleu et que l'aire du losange rouge est mesurée dans le repère rouge (çàd avec la norme rouge) ?

Elle peuvent être mesurées dans l'un ou l'autre, ça ne change rien car les transformations de Lorentz ont un déterminant de 1, cela signifie qu'en passant d'une représentation à l'autre (repère orthonormé t,x vers repère orthonormé t',x') les aires ne sont pas affectées par la transformation. C'est le cas aussi pour les rotations et les cisaillements.

m@ch3

[A voir en vidéo sur Futura]

[Sethy]

Elle peuvent être mesurées dans l'un ou l'autre, ça ne change rien car les transformations de Lorentz ont un déterminant de 1, cela signifie qu'en passant d'une représentation à l'autre (repère orthonormé t,x vers repère orthonormé t',x') les aires ne sont pas affectées par la transformation. C'est le cas aussi pour les rotations et les cisaillements.

m@ch3

Merci. Coussin avait répondu dans l'autre discussion, mais c'est un poil compliqué de suivre après le fork.

J'ai deux autres questions :

1) Si sur le graphe, la "contraction des longueurs" apparait clairement, est-ce que l'effet de "dilatation du temps" s'y retrouve également ? Si non, y a-t-il un équivalent (une réponse oui ou non me suffit, j'irai chercher) ?

2) J'interprète ce graphique comme "purement" mathématique. Je veux dire par là qu'il n'y aucun rapport entre le point d'origine et une extrémité de la barre, seule la longueur de L0 importe. Est-ce correct ?

[coussin]

La dilatation du temps se fait de la même manière. Voir ici : https://commons.wikimedia.org/wiki/F...e_Dilation.png
Au lieu de comparer des longueurs le long de (x) et (x'), on compare des longueurs le long de (ct) et (ct').

Vous pouvez mettre, en effet, l'origine du diagramme où bon vous semble. Vous trouverez la même chose en appliquant le théorème de Thalès (encore un bête théorème de géométrie Euclidienne utile ici )

On peut aussi faire l'autre situation d'un barreau immobile dans (x',ct') étudié dans (x,ct). Y a un peu plus de géométrie mais on y arrive (bien sûr). Pour cette situation, il est plus facile de se mettre dans (x',ct') et on retombe sur la situation du message #1 avec alpha changé en -alpha.

[mach3]

le théorème de Thalès (encore un bête théorème de géométrie Euclidienne utile ici )

En fait ce n'est même pas de la géométrie euclidienne, ça marche déjà en géométrie affine (il y a une notion de droite = existence de géodésique mais courbure nulle, mais pas de métrique), du coup ça marche dans toute géométrie plane quelque soit la métrique. Bien pratique.

m@ch3