Bonjour,
Je comprends très bien l’interprétation actuelle qui explique que la puissance motrice assume la totalité des pertes plus la puissance utile de la charge. C’est actuellement correcte, car à ma connaissance, aucune machine n’équilibre la réaction à son action.
Pourquoi ne pas se poser la question*: que se passerait-il si une machine équilibrait la réaction à son action*? Parce-que c’est impossible, pas si sur*!
Voici mon hypothèse*pour un alternateur à aimants permanents
La fcém d’un alternateur actuel en charge se transforme en un couple mécanique que je nomme (Cfcém). Ce Cfcém associé à la rotation ω en rad/s, est une puissance opposée à la motricité.
En conséquence*: La motricité d’un alternateur en charge, compense les pertes mécaniques et la puissance du (Cfcém), pour garantir la rotation (ω).
L’énergie transformée dans la charge, est donc produite par l’induction électromagnétique de l’inducteur. Induction due au (Φ) inducteur constant et à (ω) responsable du Δ de (Φ) en du Δ de temps (t). Les Δ n’ont besoin que de (ω) pour être effectifs, sans autre énergie supplémentaire.
Comment échapper au Cfcém : La puissance (P) en Watts est une unité d’énergie par seconde.
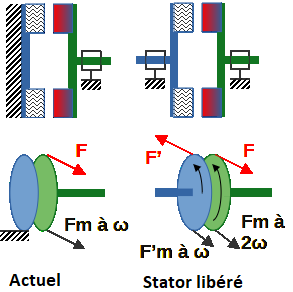
Je libère le stator qui devient le rotor bleu. Un moteur fait tourner le rotor bleu à ω et un autre moteur fait tourner le rotor vert à 2ω.
Les moteurs tournent dans le même sens. Le Cfcém (flèches rouges F’ et F) interagirait entre le rotor induit et le rotor inducteur, pour s’opposer (figer les rotors) par rapport au mouvement relatif (≠ω) entre les rotors.
Nous aurions deux couples égaux et de sens opposé (F’*r) et (F*r) sur chaque rotor. Sous condition que le rotor bleu (à ω), ait une masse d’un poids quatre fois supérieure au rotor vert (à 2ω). Afin qu’ils aient la même énergie cinétique.
La force opposée à la rotation a le signe mathématique moins (-F)
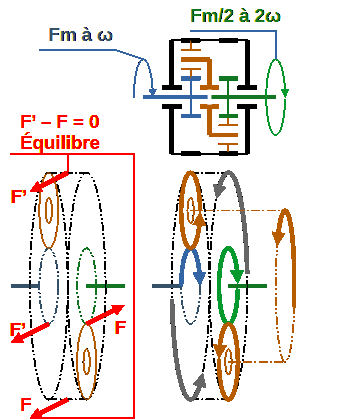
Ces deux couples (F'*r) et (-F*r) peuvent-être équilibrés dans un système d’engrenages
Toutes les pièces sont libres*: couronne noire, pignons satellites et porte-satellites oranges, ainsi que les planétaires bleu et vert.
Rôles des engrenages sur les planétaires bleu et vert.
_ Autoriser les axes bleu et vert à tournent dans le même sens.
_ Autoriser un des deux axes bleu ou vert à tourner quand l’autre est libre ou à l’arrêt.
_ Interdire la rotation inverses des axes bleu et vert.
A vide, les engrenages tournent alors dans le vide, sans perturber la rotation des moteurs. Car sans appuis fixe, les engrenages ne peuvent transmettre l’énergie d’un moteur vers l’autre.
En charge, les deux rotors reçoivent le Cfcém, qui tente de les faire tourner en sens inverse.
Les engrenages bloquent ces puissances de rotations inverses et équilibrent le Cfcém. La puissance mécanique du (Cfcém) est incapable d’influencer les motricités des planétaires bleu et vert, sous condition d’une même énergie cinétique, (F’*r*≠ω) + (-F*r*≠ω) = 0
Le Cfcém équilibré, serait alors incapable d’influencer les motricités, qui n’assumaient que les pertes mécaniques, bien que l’alternateur soit en charge.
Je passe sur le concept imaginé, car cela reste une hypothèse sans expérimentation effectuée.
Bilan des énergies :
Actuellement écrire que : P moteur = (P pertes totales + P de transformation dans la charge), c’est supposer que, P induite = 0. C’est nier l’induction avérée.
Avec l’alternateurbis-rotors :
P induite - (P pertes autres + P de transformation dans la charge) = 0
P du Cfcém = P du Cfcém/2 – P du Cfcém/2 = 0 (Cfcém équilibré)
P motrice – P pertes mécaniques = 0 => ω reste effectif et garantit les Δ deΦ et Δ de (t) inducteur.
Toutes les puissances sont prises en compte. Le (≠ω) maintient le (ΔΦ/Δt) inducteur, sans autre énergie supplémentaire. L’environnement de l’induction électromagnétique reste identique.
Reste la question: d’où viendrait l’énergie de l’induction électromagnétique responsable de la fém, transformée en (U*I), qu’est l’énergie de charge ?
-----