triangle rectangle hyperbolique et la métrique de Schwarzschild

[phys4]

En cas de reschift et en cas de blueschift
comment obtiens t'on ?

J'ai l'impression que ce schéma est un cas particulier non généralisable, comment le construire dans le cas général ?

La relation exacte entre et (z+1) est


ou encore
-----

[Mailou75]

Voici un shéma.

Attention ta droite rouge n'est pas perpendiculaire à OA !

Le segment rouge intersecte [OB] en B'
Je me demande si [OB]/[OB'] = [AB] / [AB'] et si ce rapport est lui même égal à Xv

Non, voir schéma joint :
OA=1 AC= OD= BD=
Donc OD/OA=BD/AC= (=OB/OC)
Donc la valeur AB/AC n'a rien de remarquable

comment obtient on ?

? Joker

pour l'énergie d'un photon est :

donc
En cas de reschift et en cas de blueschift

Dans cet exemple =0.8 donc z+1 (=3.00) et (=1.66) sont différents, ton égalité est étrange

A+
Mailou

[Zefram Cochrane]

Bref, tout ceci est plutôt amusant et intrigant... mais ça ne répond pas aux questions :
-Pourquoi est-ce que je ne trouve pas : longueur de l'arc AB = arcosh (produit scalaire hyperbolique OA.OB) ?
-Peut-on lire ds² quelque part ou je suis hors sujet ?

Mailou

Ca y"est je peux répondre à ta question.
Tu ne trouve pas ton égalité parce que le triangle OAB (message 6) ne correspond pas à un triangle hypberbolique.
soit a eb b deux angles.
tu as :




le produit scalaire de OA.OB donne

j'aimerai bien pouvoir placer a et b sur ton schéma du #6.
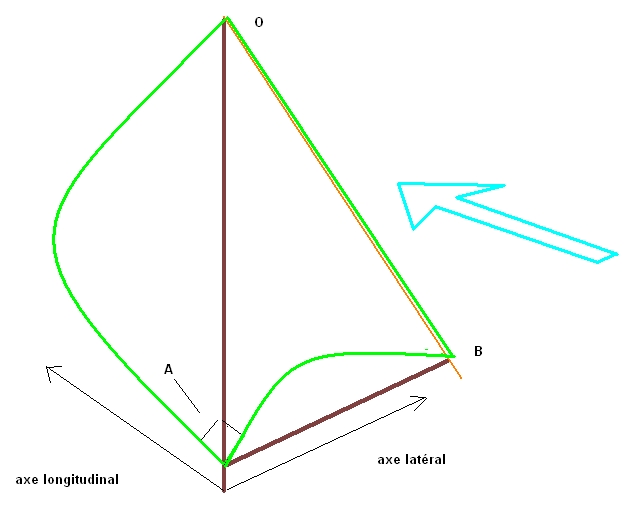
J'ai fait un schéma avec une voile hyperbolique triangle rectangle en A. la courbe OA dans l'axe longitudinal du bateau et la droite OB dans l'axe latéral. La projection place (sur l'écran) est un triangle rectangle hyperbolique en A car OA est plus grand que OB contrairement à ton schéma du #6 et c'est pour cela que tu ne retrouve pas ton égalité.

pour la relation entre et 1+Z je m'en remet à vos bon soins (Phys + toi) mais j'aimerais comprendre comment en abouti la larelation entre 1+Z et et .

SI tu es d'accord avec moi, je peut passer au message 7

Cordialement,
Zefram

[Mailou75]

Salut,

ou encore

En voilà des relations intéressantes

J'ai l'impression que ce schéma est un cas particulier non généralisable, comment le construire dans le cas général ?

Qu'entend tu par "non généralisable" ? Je reprends toujours les mêmes valeur mais elle est valable pour tout sur ]-1;+1[ (ça fait déjà pas mal )

[Mailou75]

comment le construire dans le cas général ?

Si tu veux d'autre exemples de voir la pièce jointe tirée de http://forums.futura-sciences.com/as...ace-temps.html messages #1 (voir aussi zoom #5 pour l'autre forme)

Pour la construction c'est simple exemple :
Quand =0.8 Lorentz/Minkowski nous disent que lorsque la ligne d'univers de l'objet (orange) intercepte l'espace euclidien (bleu)
il n'aura compté que jusqu'à 6, après c'est une règle de trois pour définir sa position s'il compte jusqu'à 10 (autant que l'observateur)
si on trace l'ensemble des positions de temps propre égal (10) pour différents on obtient cette fameuse courbe (pointillé gris) du type 1/x !
Puis le cône de simultanéité nous dit ce que voit l'observateur à t=10 :
un objet émis à t=0 allant à 0.8c est vu à un age 3,33 (peu importe l'unité...) et à une distance de 4,44 temps.lumière
(pour 3,33 secondes la distance est 4,44 seconde.lumière) l'horizon visible de cette expérience est à t/2=5 temps.lumière (objets allant à ->c vus à l'age ->0)
(Les petits cônes en haut montrent que dans cette représentation, la lumière va toujours à 45°, ce qui n'est pas le cas des autres figures)

J'essaye d'être le plus transparent possible en tout cas, j'espère que ceci pourra te convaincre du bienfondé de la démarche
Mailou

[Mailou75]

Ça y'est je peux répondre à ta question.
Tu ne trouve pas ton égalité parce que le triangle OAB (message 6) ne correspond pas à un triangle hypberbolique.
soit a et b deux angles. tu as :


le produit scalaire de OA.OB donne
j'aimerai bien pouvoir placer a et b sur ton schéma du #6.

Ça m’intéresse

J'ai fait un schéma avec une voile hyperbolique triangle rectangle en A. la courbe OA dans l'axe longitudinal du bateau et la droite OB dans l'axe latéral. La projection place (sur l'écran) est un triangle rectangle hyperbolique en A car OA est plus grand que OB contrairement à ton schéma du #6 et c'est pour cela que tu ne retrouve pas ton égalité.

suis perdu là

A+
Mailou

[Mailou75]

J'ai fait un schéma avec une voile hyperbolique triangle rectangle en A.

J'ai l'impression que tu tiens à tout prix à retrouver la formule de Pythagore euclidienne,
quitte à courber les droites dans une dimension inconnue pour que la plongeur des arcs obtenus vérifient l'égalité "normale".
C'est tordu ton truc

Il est plus simple d'admettre qu'un triangle rectangle "normal" dessiné dans un espace hyperbolique (OAC pour la dernière version avec les lettres)
vérifie une autre égalité OC²=OA²-AC² (Théorème de Pythagore hyperbolique), simplement

Je dis pas que la voile n'est pas une piste intéressante pour retrouver l'égalité mais pour l'heure j'ai du mal à voir comment

Mailou

[Zefram Cochrane]

ben disonsque je cherche à coller le triangle rectangle euclydien vérifiant l'équation dS² + dR'² = c²dT'² (triangle de gauche)
sur une surface hyperbolique et obtenir un triangle rectangle hyperbolique (du genre shéma joint) vérifiant l'équation dS² = c²dT²/X² - X².dR²(triangle de droite)
(dans le shéma joint : dS est en noir, dR' et dR sont en marron CdT' et CdT sont en vert.

Pour Minkovski cela ne pose pas de problème.
à partir des équations de Lorentz, tu vérifie que dS²= C²dT'² - dR'² = C²dT² - dR²
et pourtant tu as CdT = X CdT' et dR = XdR'

Zefram

[Mailou75]

Re,

Les surfaces colorées donnant une indication du redshift/blueshit valent toutes 1/2
(c'est d'ailleurs avec ça qu'on trouve , qui n'est pas représenté cette fois...)

Ici encore prend une valeur positive/négative de part et d'autre de A (observateur)

La nouvelle relation donnée par Phys4 ( merci) se vérifie 1+ (abscisse) x (ordonnée) = z+1 (aire du rectangle hachuré en violet) !!

Le reste parle de lui même, je vais éviter de radoter

J'adore ce jeu

A+
Mailou

[phys4]

J'ai compris la construction de la droite OCB.

Toutes les fonctions hyperboliques apparaissent sur la figure, je commence à comprendre pourquoi ces fonctions ont été appelées hyperboliques, elles ont sans doute été découvertes comme longueurs caractéristiques de l'hyperbole.

Je n'ai pas trouvé la solution géométrique pour additionner des vitesse quelconques, mais la dernière figure donne une solution simple pour doubler ou diviser par 2 la vitesse sur une figure donnée, il suffit de prolonger la droite OB jusqu'à la droite d'ordonnée 1, le point d'intersection donne le nouveau point B.
Dans la figure les points B1 et B2 correspondent à une vitesse "double".

[Mailou75]

Salut,

J'ai compris la construction de la droite OCB.

Ahh ça me fait plaisir

Je n'ai pas trouvé la solution géométrique pour additionner des vitesse quelconques, mais la dernière figure donne une solution simple pour doubler ou diviser par 2 la vitesse sur une figure donnée, il suffit de prolonger la droite OB jusqu'à la droite d'ordonnée 1, le point d'intersection donne le nouveau point B.
Dans la figure les points B1 et B2 correspondent à une vitesse "double".

Effectivement, joli
Et les surfaces OAB₁=OB₁B₂=_v

Pour l'additivité de vitesses quelconques, il faut prendre la figure du message #6 de ce fil :
Un point B₁ (vitesse v₁) a pour abscisse (z+1)₁. La courbe ln(z+1) donne ₁
Un autre point B₂ (vitesse v₂) a pour abscisse (z+1)₂. La courbe ln(z+1) donne ₂
En suite on additionne ces valeurs sur l'axe y telles que ₁ + ₂ = _3
3 est une ordonnée qui donne (suivant la courbe ln) un (z+1)₃, donc un point B₃ et donc une vitesse v₃=v₁+v₂

C'est pas exactement une "construction géométrique" à la règle et au compas, mais ça marche bien grâce à la propriété de d'être additif !

(Si tu as bien compris le sens de cette figure #35, tu devrais jeter un coup d’œil à http://forums.futura-sciences.com/as...ace-temps.html message #5
parce que celle là personne ne la comprend et je me sens très seul )

A bientot
Mailou

[Mailou75]

ben disonsque je cherche à coller le triangle rectangle euclydien vérifiant l'équation dS² + dR'² = c²dT'² (triangle de gauche)
sur une surface hyperbolique et obtenir un triangle rectangle hyperbolique (du genre shéma joint) vérifiant l'équation dS² = c²dT²/X² - X².dR²(triangle de droite)
(dans le shéma joint : dS est en noir, dR' et dR sont en marron CdT' et CdT sont en vert.

Tu veux vérifier l'égalité dS² + dR'² = c²dT'² en Pythagore normal, puis projeter sur une surface courbe..?
Ça doit être possible mais pas simple...

Si tu prends la fig message #32:
Tu peux te dire que OA et OB sont comme les rayons d'un cercle, ils sont égaux : OA=OB=ct
Ces sont les lignes d'univers des objets (OB), ou l'axe de temps si l'objet est l'observateur (OA)
Si on définit A comme observateur, avec B ayant une vitesse relative non nulle,
l'espace euclidien de A engendre un point C tel que OC=s=c (et AC=d)
Pour A l'observateur, B parcourt d en un temps t
Or ce qui nous intéresse est uniquement de situer le point C sur la droite OB, cad de connaitre : OB/OC=t/=

Tu te complique la vie avec ton voilier je crois
A+
Mailou

[Mailou75]

(Si tu as bien compris le sens de cette figure #35, tu devrais jeter un coup d’œil à http://forums.futura-sciences.com/as...ace-temps.html message #5
parce que celle là personne ne la comprend et je me sens très seul )

Vous allez me trouver un peu lourd avec cette analogie, mais j'insiste une dernière fois :
Si on fait l'analogie entre le Big Bang et une explosion, et si ces figures sont l'image d'une explosion dans le vide =
Les objets sont projetés à des vitesses différentes (0 à c) et conservent cette vitesse relative au cours du temps
Alors dans la figure #35 (Minkowski) il faut placer l'observateur au centre de l'explosion (il a une position fixe dans l'espace entre t=0 et t=10)
Et il parait inconcevable (tant pis pour l'église) que l'homme puisse réellement être au centre d'une "explosion primordiale"
D'où l’intérêt de la figure #5 (et #6 du lien) qui offre les mêmes résultats mais avec une interprétation qui peut être différente :
L'espace (cercle) augmente au cours du temps, et le choix d'une ligne d'univers (rayon) en tant qu'observateur, en fait un axe de temps
avec comme conséquence une impression d'explosion dont nous serions au centre
Ce n'est finalement qu'une illustration de l'image du ballon qui gonfle pour l'expansion...
Pour un espace 2D, surface d'une sphère, l'espace temps 2D+t est le volume de la boule
Et l'observateur voit une "coupe" de ce volume : son cône passé !

Bon désolé c'est un peu HS
Mailou

[Zefram Cochrane]

Bonsoir,
j'ai éssayé de paramétrer l'équation des champs de la métrique de Schwarzschild sur le modèle des équations de Lorentz dans le cadre d'une trajectoire radiale.

voici ce que cela donne :



je ne sais pas si on peut en tirer quelque chose, mais à priori ça marche.
Cordialement,
Zefram

[Mailou75]

(...)vérifiant l'équation dS² = c²dT²/X² - X².dR²
(...)
à partir des équations de Lorentz, tu vérifie que dS²= C²dT'² - dR'² = C²dT² - dR²
et pourtant tu as CdT = X CdT' et dR = XdR'

En fait je crois que tu mélanges plusieurs choses, et que ça touche à la synchronisation (voir pièce jointe) :

-D'une part, on trace un repère fixe (bleu) abscisse d et ordonnée t (on travaille avec c=1, ct=t)
Puis on trace le repère (rouge)d'un observateur au même endroit animé d'un vitesse 0,5c
D'une certaine façon qui va encore faire bondir Amanuensis (projections en vert) on peut dire que pour l'observateur fixe,
le voyageur a un temps dilaté t'=t et un espace contracté dans le sens du mouvement d'=d/

-D'autre part, si on situe un évènement avec un s, cette valeur est invariante par changement de repère
Ainsi s²=c²t²-d² que l'on simplifie pour c=1 en s²=t²-d²
nous dit que pour l'observateur fixe l'évènement se situe à d=0,8sl et t=1s, soit
et que pour l'observateur mobile (0,5c) l'évènement est à d~0,35sl et t~0,69s, soit

Il faut donc se méfier de ce s c'est plus que d'un observateur en mouvement
et savoir de quel s tu parles dans tes équations !
Enfin, tout ça si je raconte pas encore des fables...

Voir http://forums.futura-sciences.com/as...n-temps-8.html mess #109 pour une image plus sympa

j'ai éssayé de paramétrer l'équation des champs de la métrique de Schwarzschild sur le modèle des équations de Lorentz dans le cadre d'une trajectoire radiale.
voici ce que cela donne :

A+
Mailou

[Zefram Cochrane]

Bonsoir,
pour établir les équations
j'ai posé :
CdT' = A(CdT + BdR)
dR' = D(CdT + EdR)

Je me suis retrouvé avec trois équation, d'où le coeff A (alpha)
à savoir :
A² - D²E² = 1/X²
D² - A²B² = X²
2A²B = 2D²E

Pour trouver A (alpha) en fonction de X (gamma) je pense utiliser une trajectoire de genre lumière.
Cordialement,
Zefram

[Mailou75]

Salut Zef,

Je ne comprends pas ce que tu fais désolé

Sinon voilà l'autre moité du dessin pour l'invariance de s, j'espère ne pas me tromper...

A+
Mailou

[Zefram Cochrane]

Bonsoir,
j'ai éssayé d'écrire les transformations de Lorentz dT'= F(X;CdT;dR) et dR'=G(X; dR;CdT) qui correspondent à l'équation des champs dans la métrique de Schwarzchild pour une trajectoire radiale de genre temps.
J'ai posé :
CdT' = A(CdT + BdR)
dR' = D(dR + ECdT)

(CdT')² - dR'² = A²(CdT)² + A²B²(dR)² + 2A²B(CdTdR) - D²(dR)² - D²E²(CdT)² - 2D²E(CdTdR)
dans la métrique de Schwarzschild, on a :
(CdT')² - dR'² = 1/X² (CdT)² + X² (dR)²
on a donc trois équations pour quatre inconnues :
A² - D²E² = 1/X²
D² - A²B² = X²
et A²B = D²E

On isole dans un premier temps E, puis D, et B. On obtient donc CdT' = F(A ; X; CdT ; dR) et dR' = G(A ; X ; CdT; dR)
pour avoir une solution unique c'est à dire pour virer A, j'ai besoins de pouvoir exprimer A = H(X)

Pour cela j'ai utilisé la solution de l'équation des champs correspondant à une trajectoire radiale de genre lumière.
une quatrième équation qui me donne pour solution A = 1/X
A =1/X
B= 0
D=X
E=0
donc CdT' = 1/X CdT
et dR' = X dR

ce n'était pas le genre de solution recherchée mais bon je trouve très drôle de comparer ces deux équations avec ce que tu décrit pour la RR dans ton message #45.
Tu m'étonnes que pour un observateur local en chute libre dans un champs de gravitation à symétrie sphérique radialement par rapport à l'observateur de référence à l'oo on trouve dR'=dR et dT'=dT

Je pense que d'une certaine façon, il y a matière à réflexion.
Cordialement,
Zefram

[Zefram Cochrane]

J'ai compris la construction de la droite OCB.

Toutes les fonctions hyperboliques apparaissent sur la figure, je commence à comprendre pourquoi ces fonctions ont été appelées hyperboliques, elles ont sans doute été découvertes comme longueurs caractéristiques de l'hyperbole.

Je n'ai pas trouvé la solution géométrique pour additionner des vitesse quelconques, mais la dernière figure donne une solution simple pour doubler ou diviser par 2 la vitesse sur une figure donnée, il suffit de prolonger la droite OB jusqu'à la droite d'ordonnée 1, le point d'intersection donne le nouveau point B.
Dans la figure les points B1 et B2 correspondent à une vitesse "double".

Bonjour,
Vu que la tangeante au point A intersecte l'abscisse au point 2 et l'ordonnée au point 2. que la droite intersectant l'abscisse au point 4 et l'ordonnée au point 1 est aussi tangeante à la courbe au point B3. J'imagine comme le disait Mailou en réponse, que

la surface de OAB3
la surface de OAB1
la surface de OB1B3

C'est possible de représenté l'additiivté des vitesse quelconques mais faut passer par des échelles logarithmiques
Cordialement,
Zefram

[invite60be3959]

Bonjour,

Bonsoir,
j'ai éssayé de paramétrer l'équation des champs de la métrique de Schwarzschild sur le modèle des équations de Lorentz dans le cadre d'une trajectoire radiale.

voici ce que cela donne :



je ne sais pas si on peut en tirer quelque chose, mais à priori ça marche.
Cordialement,
Zefram

Je ne veux pas casser l'ambiance, mais je pense que tu ne sais même pas trop ce que tu fais ! Et pourquoi ? Dans quel but ? Peut-être cherches-tu une nouvelle formule, mais tu ne la trouveras jamais en bidouillant des formules existantes.

[Zefram Cochrane]

Je voulais exprimer CdT et dR' en fonction de CdT' ; dR' ; .
L'objectif est (était) de pouvoir projeter un triangle rectangle euclydien ou hyperbolique formé des cotés CdT' et dR' et dS sur une forme hyperbolique déterminée par les équations obtenues et de pouvoir retrouver géométriquement CdT et dR.
A première vue les équations recherchées sont :

et

Il y a une erreur dans le raisonnement ou la méthode employée au #48?
Cordialement, Zefram

[Mailou75]

Salut,

Le calcul est plaisant, en tout cas ça a l'air juste, mais je bloque sur deux points...

J'ai posé :
CdT' = A(CdT + BdR)
dR' = D(dR + ECdT)

(...)j'ai besoin de pouvoir exprimer A = H(X)
Pour cela j'ai utilisé la solution de l'équation des champs correspondant à une trajectoire radiale de genre lumière.
une quatrième équation qui me donne pour solution A = 1/X

Ca me dépasse, mais comme le fait remarquer Vaincent, j'espère que tu sais ce que tu es en train de faire

J'ai essayer d'imaginer F et G comme des points, mais j'ai vite été largué surtout qu'a la fin ils ont des coordonnées identiques ..?

dT'= F(X;CdT;dR) et dR'=G(X; dR;CdT)
(...)
CdT' = F(A ; X; CdT ; dR) et dR' = G(A ; X ; CdT; dR)

A première vue les équations recherchées sont :

et

Surtout que si c'est pour obtenir ça c'est étrange, j’espère que ta fonction A=H(X) peut avoir d'autres propriété
Bon en tout cas je suis largué sur ta démonstration

Bonjour,
Vu que la tangeante au point A intersecte l'abscisse au point 2 et l'ordonnée au point 2. que la droite intersectant l'abscisse au point 4 et l'ordonnée au point 1 est aussi tangente à la courbe au point B3. J'imagine comme le disait Mailou en réponse, que

la surface de OAB3
la surface de OAB1
la surface de OB1B3

Euh... non comment tu construis B1 dans ton exemple ?

Ce que tu fais là c'est uniquement définir un B3 qui correspond à =0,6
En fait si on appelle Xn et Ym les points d'abscisse et d'ordonnée n et m
Alors tout ce que tu peux dire c'est que ces surfaces sont égales : OAX₂=OAY₂=OBX₄=OBY₁
Mais tu n'additionne rien... enfin j'ai pas compris sinon

En quelque sorte, ta nouvelle droite Y₁X₄ c'est l'espace et OY₁X₄ c'est la surface du "cône d'espace temps"
qui est invariante : OY₂X₂=OY₁X₄=2 !

Mais c'est une propriété fort intéressante, l'espace (Y₁X₄) est tangent à la courbe de temps propre constant pour tous les observateurs
et OB c'est le nouvel axe de temps de l'objet en mouvement... c'est d'ailleurs la compréhension de ceci qui m'a permis de débloquer mes problème sur l'aberration de la lumière
(qq jours le temps de la dessiner et je vous la livre...)

C'est possible de représenter l’additivité des vitesse quelconques mais faut passer par des échelles logarithmiques

?? No need ?? je me cite mess #41:

Pour l'additivité de vitesses quelconques, il faut prendre la figure du message #6 de ce fil :
Un point B₁ (vitesse v₁) a pour abscisse (z+1)₁. La courbe ln(z+1) donne ₁
Un autre point B₂ (vitesse v₂) a pour abscisse (z+1)₂. La courbe ln(z+1) donne ₂
En suite on additionne ces valeurs sur l'axe y telles que ₁ + ₂ = _3
3 est une ordonnée qui donne (suivant la courbe ln) un (z+1)₃, donc un point B₃ et donc une vitesse v₃=v₁+v₂
C'est pas exactement une "construction géométrique" à la règle et au compas, mais ça marche bien grâce à la propriété de d'être additif !

Enfin pour ces questions de s invariant et du Pythagore hyperbolique s²=c²t²-d²
qui est une formule très peu intuitive, je te propose de considérer que l'égalité peu être vue en surfaces, encore...
Dans le schéma du message #47, le carré rouge a la même surface que le losange rouge !
Et le petit rectangle (rouge) dont la diagonale est notée s a la même surface que le losange correspondant dans la figure de droite !!
C'est plus facile à digérer que les s²... enfin je trouve

A+
Mailou

[Mailou75]

Re,

Ci joint un p'tit schéma récapitulatif avec quelques valeurs numériques, qui montre comment on y additionne les vitesses relativistes

Question : si un objet se dirige vers moi à 0,4c tandis qu'un autre s'éloigne à 0,6c
à quelle vitesse ces objets se voient ils s'éloigner l'un de l'autre ?
Réponse : V=0,26c (Formule classique V=(v+w)/(1+v.w/c²) avec v=0,6c et w=-0,4c)

Sinon, sur le graph ça donne ₁+₂=₃ et avec ₃ on "construit" ₃
La courbe ln x est juste une bidouille pour additionner (ou soustraire) les surfaces...
Le calcul équivalent c'est ₃=tanh(tanh^-10,6+tanh^-1-0,4)=0,26

En violet on retrouve les constructions dont parlait Phys4 qui permettent,
en se servant des droites x=1 ET y=1, d'obtenir le double ET la moitié d'une vitesse
Ex : Pour B₁ qui va à 0,6c on trouve B₄ pour la moitié (0,33c) et B₅ pour le double (0,88c)

Et alors là c'est fumant je suis tombé sur une relation excellente : pour x un "multiple de vitesse"
Ex : z+1_0,6=2
z+1_2.0,6=z+1_0,6²=² soit z+1_0,88=4
z+1_0,6/2=z+1_0,6^1/2=2^1/2 soit z+1_0,33=
Par extension 0,33+0,33+0,33 -> 0,77 se vérifie : z+1_3.0,33=z+1_0,33³=z+1_0,77 d'où la formule générale...
Ça doit sans doute pouvoir se retrouver mathématiquement, en tout cas j'aime bien

A bientôt
Mailou

[invite60be3959]

Salut,

On va essayer de reprendre tout depuis le début pour y voir plus clair.

Je voulais exprimer CdT et dR en fonction de CdT' ; dR' ; .

Déjà, n'utilise pas de majuscules car elles signifient autre chose en physique. Si on en revient à ton 1er message, il y a une erreur dès le départ :

Puis que la vitesse de la lumière est constante dans le référentiel du mobile R' et dans celui de lo'bservateur fixe R je peux écrire :




d'où
on pose

on a donc

Le fait que la vitesse de la lumière soit la même dans les 2 référentiels ne te donne pas du tout le droit d'écrire tes 2 premières formules car tu vois bien qu'il y a une contradiction entre celles-ci et la dernière (qui elle est bonne si l'on suppose que R' est le système de référence).

La relation est issue de la transformation de Lorentz qui permet de passer de R à R' et pas de ton calcul. En fait tu écris des choses fausses, qui en les bidouillants comme il faut, t'ammènent à des choses bonnes. Cela n'empêche pas néanmoins que les arguments sensés fonder le raisonnement soient faux. Ce n'est pas du tout ça la méthode scientifique. Ce n'est pas parce qu'un résultat est bon, que les arguments qui ont permis d'y parvenir sont eux aussi corrects. En plus tu fais tout un petit calcul pour finalement arriver la formule bien connue de la dilatation du temps, à quoi cela sert-il ? Á rien!

Ensuite(toujours dans ce message #1) tu écris :

si
puis-je affirmer :

où ?

or tu devrais savoir que la métrique pseudo-euclidienne ds² est un invariant relativiste et donc que :



Surtout que cela fait parti des fondamentaux de la RR. Ce qui amène très sérieusement à se demander si tu sais vraiment ce que tu es en train faire! Et ce dès le début.

Dans ton dernier message, les objectifs paraissent plus clairs:

L'objectif est (était) de pouvoir projeter un triangle rectangle euclidien ou hyperbolique formé des cotés CdT' et dR' et dS sur une forme hyperbolique déterminée par les équations obtenues et de pouvoir retrouver géométriquement CdT et dR.
A première vue les équations recherchées sont :

et

L'erreur est de vouloir faire ça en 3D alors que ce n'est pas nécessaire ici(tu as 2 coordonnées : r et t). Pas besoin de projeter un triangle sur un hyperboloïde. En RR, on peut toujours réduire le problème à une dimension d'espace et une dimension de temps.
Quant aux équations recherchées, elles n'étaient pas recherchées puisques connues de tous ! (dilatation du temps et contraction des longueurs), à ceci près que celles que tu écris sont inversées. Si R' est le système de référence :



En fin de compte ce que tu cherchais à faire(en restant dans le cadre de la RR), c'était de retrouver ces relations sur un graphique, ce que fait justement un diagramme de Minkowski, et c'est ce qu'à fait Mailou75 depuis le début(même si bien souvent ces shémas étaient beaucoup trop chargés pour être suffisament compréhensibles!). Tu peux par exemple aller voir ce lien où les diagrammes de Minkowski sont très bien expliqués.

Et oublie la métrique de Schwarzchild, car là c'est beaucoup trop compliqué pour ce représenter les choses, à moins de s'initier aux diagrammes de Penrose.

[Mailou75]

Salut,

(...) et c'est ce qu'à fait Mailou75 depuis le début (même si bien souvent ces schémas étaient beaucoup trop chargés pour être suffisamment compréhensibles!)

Voilà qui me rassure, merci
Désolé pour la complexité, j'essaye pourtant d'être le plus communicatif possible avec les couleurs etc... mais c'est vrai que quand on a pas fait la construction ça peut paraitre obscur

Et oublie la métrique de Schwarzchild, car là c'est beaucoup trop compliqué pour ce représenter les choses, à moins de s'initier aux diagrammes de Penrose.

Next lesson, yeah
Ça à l'air coton, mais c'est sans doute à première vue... (comme le lien que tu donne pour la RR, parfaitement indigeste pour moi : intégrales, matrices...)
Je ne désespère pas de pouvoir y comprendre qq chose.. un jour

A+
Mailou

[Mailou75]

(...) je suis tombé sur une relation excellente : pour x un "multiple de vitesse"

Ben tout compte fait c'est c'est pas une trouvaille
Mais ça veut quand même dire que c'est une forme d'additivité des vitesses :
₁ + ₂ = ₃ peut être remplacé par (z+1)₁ x (z+1)₂ = (z+1)₃

Je viens à peine de capter celle là...
Dans l'image du message #7 de la discussion http://forums.futura-sciences.com/as...e-lumiere.html,
les longueurs des droites rouge et bleue sont respectivement z+1 et 1/z+1 et le grand axe de l'ellipse vaut 2

A+
Mailou

[Zefram Cochrane]

Bonjour,

Salut,

On va essayer de reprendre tout depuis le début pour y voir plus clair.


Déjà, n'utilise pas de majuscules car elles signifient autre chose en physique. Si on en revient à ton 1er message, il y a une erreur dès le départ :

J'utilise les majuscules dans mes messages pour plus de lisibilité c'est tout. Je vais faire sans dans celui-ci.

Le fait que la vitesse de la lumière soit la même dans les 2 référentiels ne te donne pas du tout le droit d'écrire tes 2 premières formules car tu vois bien qu'il y a une contradiction entre celles-ci et la dernière (qui elle est bonne si l'on suppose que R' est le système de référence).


La relation est issue de la transformation de Lorentz qui permet de passer de R à R' et pas de ton calcul. En fait tu écris des choses fausses, qui en les bidouillants comme il faut, t'ammènent à des choses bonnes. Cela n'empêche pas néanmoins que les arguments sensés fonder le raisonnement soient faux. Ce n'est pas du tout ça la méthode scientifique. Ce n'est pas parce qu'un résultat est bon, que les arguments qui ont permis d'y parvenir sont eux aussi corrects. En plus tu fais tout un petit calcul pour finalement arriver la formule bien connue de la dilatation du temps, à quoi cela sert-il ? Á rien!

Je suis étonné que tu dises que mon raisonnement est faut pas d'accord avec toi car ce sont les formules qui décrivent l'expérience de pensée des photons qui rebondissent du sol au plafond dans un train en mouvement par rapport à l'observateur du quai. A quoi ça sert? Parce que j'ai un dicton :
Savoir un résultat, c'est bien, comprendre pourquoi ce résultat, c'est mieux (même si parfois le mieux est l'ennemi du bien).

Je suis d'accord avec toi sur le fait que la référence, ce sont les transformations de Lorentz. C'est parce que je ne m'y suis pas référé que j'ai commis l'erreur que tu cites ci-dessous.

or tu devrais savoir que la métrique pseudo-euclidienne ds² est un invariant relativiste et donc que :



Surtout que cela fait parti des fondamentaux de la RR. Ce qui amène très sérieusement à se demander si tu sais vraiment ce que tu es en train faire! Et ce dès le début.




Quant aux équations recherchées, elles n'étaient pas recherchées puisques connues de tous ! (dilatation du temps et contraction des longueurs), à ceci près que celles que tu écris sont inversées. Si R' est le système de référence :

Dans le cadre de la RG : j'ai essayé d'écrire sur le modèle des transformations de Lorentz et TEX]dr'[/TEX] à partir de l'équation des champs dans la métrique de Schwarzchild pour une trajectoire radiale de genre temps.



J'ai posé :



ce qui donne normalement :


on a donc trois équations pour quatre inconnues :
A² - D²E² =
D² - A²B² =
et A²B = D²E

J'ai obtenu dans un premier temps :



Pour avoir A, j'ai utilisé l'équation des champs pour une trajectoire radiale de genre lumière ce qui me donne :


d'où
B = 0

E=0




Quatre équations à quatre inconnues implique qu'il y ait une une et unique solution pour chacune des inconnues.

Dans ton dernier message, les objectifs paraissent plus clairs:


L'erreur est de vouloir faire ça en 3D alors que ce n'est pas nécessaire ici(tu as 2 coordonnées : r et t). Pas besoin de projeter un triangle sur un hyperboloïde. En RR, on peut toujours réduire le problème à une dimension d'espace et une dimension de temps.
Quant aux équations recherchées, elles n'étaient pas recherchées puisques connues de tous ! (dilatation du temps et contraction des longueurs), à ceci près que celles que tu écris sont inversées. Si R' est le système de référence :



En fin de compte ce que tu cherchais à faire(en restant dans le cadre de la RR), c'était de retrouver ces relations sur un graphique, ce que fait justement un diagramme de Minkowski, et c'est ce qu'à fait Mailou75 depuis le début(même si bien souvent ces shémas étaient beaucoup trop chargés pour être suffisament compréhensibles!). Tu peux par exemple aller voir ce lien où les diagrammes de Minkowski sont très bien expliqués.

Et oublie la métrique de Schwarzchild, car là c'est beaucoup trop compliqué pour ce représenter les choses, à moins de s'initier aux diagrammes de Penrose.

Étrangement, si mes relations sont exactes, effectivement, on peut se contenter des diagrammes de Minkovski, ou des diagrammes de Mailou.
Mais si dans la métrique de Schwarzchild,


Quel est l'intérêt des diagrammes de Penrose? Comment s'y initier tu as des liens à recommander?
Cordialement,
Zefram

[Mailou75]

(z+1)₁ x (z+1)₂ = (z+1)₃

Ça veut dire que pour additionner des vitesses je multiplie leur z+1, je trouvais la relation intéressante...

[Mailou75]

(...) on peut se contenter des diagrammes de Minkovski, ou des diagrammes de Mailou.

C'est la même chose !! J'ai rien inventé moi, je découvre c'est tout

Ça veut dire que pour additionner des vitesses je multiplie leur z+1, je trouvais la relation intéressante...

Et c'est pour ça que j'aime bien savoir si les équivalences, sur lesquelles je tombe par hasard, sont avérées... ou pas (?)

A+
Mailou

[Zefram Cochrane]

Tu redécouvres.
SI tu as fait les calculs qui sont apparamment justes, alors ils ont avérés.
Maintenant il faudrait je crois faire la synthèse de tout ceci, ce qui devrait nous donner une bonne conception de la métrique de Minkovski et de la RR.
Cordialement,
Zefram