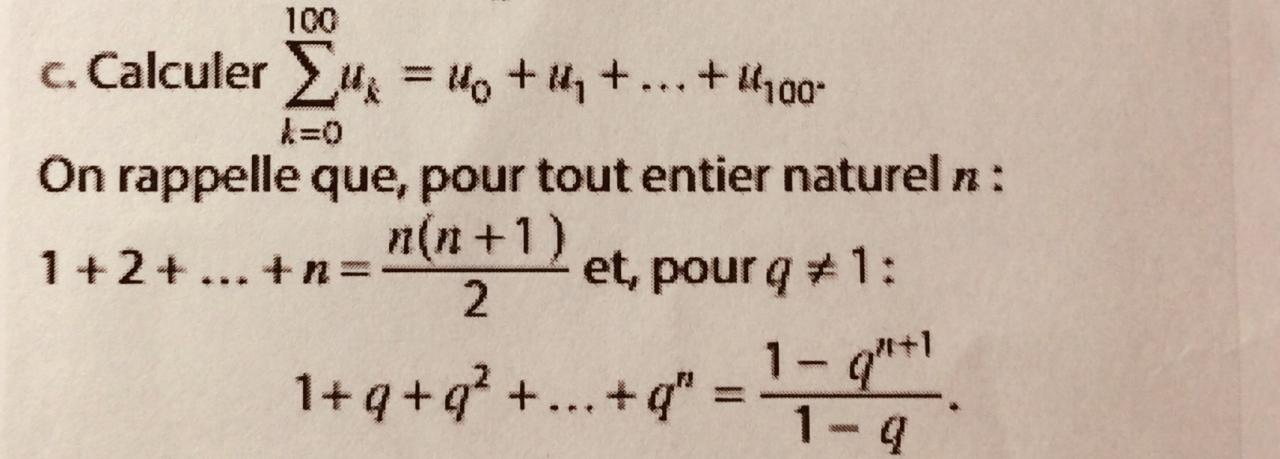Exercice suite terminal

[Lachimiecphysique]

Bonsoir, j’ai besoin de votre aide pour l’exercice suivant qui traite les aspects des suites :

On considère la suite (u_n)définie par u₀= 0 et on a pour tout entier naturel n, u_n+1= 3u_n-2n +3

Les questions :

1) Calculer u₁ et u₂
2) Démontrer par récurrence que pour tout entier n, u_n supérieur ou égal
3) En déduire que la suite (u_n) est croissante
4) Soit la suite (v_n) définie pour tout entier naturel n par v_n= u_n - n + 1
a. Essayez de démontrer que la suite (v_n) est une suite géométrique de raison 3.
b. En déduire que pour tout entier naturel n:
u_n= 3_n+n-1
Je vous mets la question 4)c. en image

d. Écrivez un algorithme en langage naturel qui calcule la somme ci-dessus


Mes réponses :

1) u₁=3*0 - 2*0 +3 =3
u₂= 3*3-2*1+3= 10

2) Soit (u_n) une suite définie à l’aide d’une relation de récurrence :
u_n+1= 3u_n - 2n +3

étape 1 : initialisation

(J’ai repris u₁)Pour n=1, on a u₀₊₁= 3u₀-2*0+3
Donc u₁= 3*0-2*0+3 =3
Ici l’initialisation est vérifié car u_n supérieur ou égal n

étape : Hérédité
Malgré mon cours et des recherches sur internet, j’ai dû mal à trouver des réponse , j’arrive pas à comprendre cette histoire de k et de k+1... Si quelqu’un peut m’expliquer clairement ceci je le remercie.

Comme vous pouvez deviner je n’ai pas fait le reste de l’exercice.
Merci si vous m’aidez !
-----

[jacknicklaus]

Tu dois montrer U_n >= n (si j'ai bien compris).
l'initialisation, pas de souci; Tu l'as même avec n = 0 car U₀ = 0 >= 0

Pour l'hérédité, tu supposes vérifiée la relation au rang n, c'est à dire U_n >= n
et tu dois la vérifier au rang n+1, c’est à dire prouver U_n+1 >= n+1

Tout ce que tu as à faire pour celà c'est
1°) écrire U_n+1 = en fonction de U_n et n. C'est facile, c'est la définition même de la suite.
2°) utiliser la propriété au rang n, c'est à dire U_n >= n
3°) et bricoler un peu pour prouver U_n+1 >= n+1

[Lachimiecphysique]

Bonjour, merci beaucoup pour votre réponse et votre gentillesse .
Je vous confirme qu’il faut montrer U_n >= n

Voici ce que j’ai fait :

Initialisation (avec n=0):

D’après l’énoncé U₀=0
Donc ici l’initialisation est vérifié car U_n>= n

Hérédité :
1°) On suppose que p(n) est vraie, montrons également ceci pour p(n+1),
D’après l’hypothèse de récurrence U_n>= n, donc U_n+1>= n+1

Donc si U_n+1= 3U_n-2n+3
Alors U_n+1= U_n - (2n/3)+(3/3)
Alors U_n+1= U_n - (2n/3) + 1

On sait que U_n>n
Donc U_n-(2n/3) +1 > n -(2n/3)+1
Alors U_n+1 > n - (2n/3)+1...

Malheureusement j’ai dû me tromper car ici n-(2n/3)+1 < n+1....

Si vous pouvez me donner un petit indice je vous remercie, bonne journée

[Lachimiecphysique]

Ce 3U_n me gêne beaucoup...

[A voir en vidéo sur Futura]

[jacknicklaus]

Hérédité :
1°) On suppose que p(n) est vraie, montrons également ceci pour p(n+1),
D’après l’hypothèse de récurrence U_n>= n, donc U_n+1>= n+1

Non. ce qui suit le "donc" est précisément ce qu'il faut montrer !
Tu dois réaliser que l'hypothèse de récurrence est valable jusqu'à n, par hypothèse. Et que pour n+1, on n'en sait encore rien.

Donc si U_n+1= 3U_n-2n+3
Alors U_n+1= U_n - (2n/3)+(3/3)
Alors U_n+1= U_n - (2n/3) + 1

là c'est n'importequoi.
C'est BEAUCOUP plus simple.

par définition : U_n+1= 3U_n-2n+3
par hypothèse U_n>= n
donc 3U_n >= ???
donc 3U_n - 2n + 3 >= ???
donc U_n+1 >= ???

je te laisse poursuivre.

[Lachimiecphysique]

Bonsoir merci énormément pour votre aide .

Donc si par hypothèse U_n>=n
Alors 3U_n>= 3n
Donc 3U_n-2n + 3>= 3n-2n+3
Alors 3U_n -2n+3 >= n+3
Donc U_n+1>= n+3 ???

Cela me perturbe car on ne trouve pas U_n>= n+1 .... C’est normal ?

Bonne soirée

[gg0]

Heu...

Tu ne vois pas de rapport entre n+3 et n+1 ?

Cordialement

[Lachimiecphysique]

Bonjour, si excusez-moi j’étais fatigué hier soir ...

2) .....
Si U_n+1 >= n+3, alors U_n+1 > n+1 !
Donc U_n+1 >= n+1.
Donc ici P(n+1) est vraie .

Conclusion:

P(0) est vraie et P(n) est héréditaire à partir du rang 0, donc par récurrence P(n) est vraie pour tout entier n>= 0

3) On sait que U_n+1- U_n= constante

On connaît U_n+1;>= n+3 et U_n>= n.
Donc U_n+1- U_n = n+3-n = 3.

3>0 donc U_n+1- U_n>0 c’est-à-dire U_n+1>U_n, (U_n) est donc une suite croissante.


4)a) V_n+1/V_n = q

Alors V_n= U_n- n +1
Donc V_n+1= U_n+1- n +1-1
Donc V_n+1= 3U_n-2n+3-n
Donc V_n+1 = 3U_n-3n+3

Alors V_n+1/V_n = 3U_n-3n+3/U_n-n+1 = 3(U_n-n+1)/U_n-n+1
= 3 !

(V_n) est donc bien une suite de raison 3

4)b) Nous avons donc une suite V_n=V₀*qⁿ où:* q=3
*V₀= U₀- 0 + 1 = 0-0+1 =1
Alors V_n= 1*3ⁿ=3ⁿ

On sait que V_n = U_n-n+1
Donc 3ⁿ= U_n-n+1
Donc Un= 3ⁿ +1-1

c) (Voir image de l’énoncé)
Ici je sais que :
-nous avons 101 termes de U_n (De U₀ jusqu’à U₁₀₀)
-que 1 + 2+.... +n = n(n+1)/2 = Nombre de termes *(1er terme + Dernier terme)/(2)
- que 1+q etc...
Mais U_n est ni géométrique et ni arithmétique.... Comment peut-on alors calculer sa somme ? Il faut faire un mélange des formules des sommes des suites géométriques et arithmétiques ?

Merci beaucoup pour votre aide, bonne journée.

[Lachimiecphysique]

PS: À la 4)b) je trouve bien U_n=3ⁿ+n-1 au lieu de U_n= 3ⁿ+1-1, désolé pour la faute de frappe...

[ansset]

bjr, il faut déjà faire l'exercice 4), qu'as tu fait ?
le 4) abouti à Un=3ⁿ+n-1 ( et pas 3_n...)
du coup Un est constituée de deux suites séparées dont l'une est géométrique et l'autre algébrique.
suites que l'on peux additionner séparément.

ps : attention à l'origine d'une des deux.

[Lachimiecphysique]

Bonjour merci beaucoup pour votre réponse.
J’ai donc divisé U_nde cette façon :
-A_n= n-1 qui est la suite algébrique ( ou arithmétique)
-B_n= 3ⁿ qui est la suite géométrique.

*Donc S_An = Nombre de termes * (1er terme + Dernier terme)/2 où
A₀= 0-1 = -1
A₁₀₀= 100-1=99

Alors on a 101*(-1+99)/(2)=4949
Donc S_An= 4949


*Donc S_Bn= 1er terme * (1-q^{nombre de termes})/(1-q) où
B₀= 3⁰=1


Donc S_Bn= 1*(1-3¹⁰¹)/(1-3) = (1-3¹⁰¹)/(1-3)

Donc S_Un= S_An + S_Bn
Donc S_Un = 4949 +(1-3¹⁰¹)/(1-3) ~ 7,730662811*10⁴⁷?? Est-ce correct ?

4)d) Sinon j’ai essayé pour l’algorithme, voici ce que j’ai fait :
u<—0
pour k allant de 0 à 100
u<— A+B


Merci encore

[ansset]

bonjour,
j'obtiens les même résultats pour les sommes.
en revanche, je ne comprend pas ton 4 d).

[ansset]

ps : à moins que cela soit demandé, il n'est pas nécessaire de donner une valeur approchée pour la somme.

[Lachimiecphysique]

Bonjour, merci énormément pour votre confirmation pour la 4)c).

Pour la 4)d) j’ai réfléchi de la façon suivante:

- La suite (u_n) est définie par u₀=0
-La somme va de u₀ à u₁₀₀, donc on a un réel k qui se situe de 0 à 100.
-Ensuite j’ai mis u <—- A+B car j’ai séparé la suite (u_n) en 2 partie dans la 4)c) : A_n= n-1 et B_n= 3ⁿ
Donc j’ai traduis S_Un= S_An + S_Bn par u<—- A+B (Je ne sais pas si c’est sensé dans un algorithme mais je l’ai quand même fait...)

Je trouve donc l’algorithme suivant :

u<—0
pour k allant de 0 à 100
u<— A+B

Merci si vous me donner un indice pour le fonctionnement de cet algorithme, bonne journée

[ansset]

OK, mais (vielle habitude ) le ne connais pas le signe <-? ( dans beaucoup de logiciel ="égal" suffit. )
supposons que ce soit simplement "je remplace u".
alors même dans ce cas , il faut préciser ce que sont A et B ( en fait des A_k et des B

[jacknicklaus]

u<—0
pour k allant de 0 à 100
u<— A+B[/B]

Au moins 2 erreurs fatales :

1) Cet algorithme s'arrête immédiatement en erreur avec un message type du genre "variables A et B inconnues"

2) quand bien même A et B seraient explicités correctement dans le programme, cet algorithme met 0 dans U. Puis il met les valeurs de A et B pour k = 0 dans U. (on se demande bien à quoi ca sert de commencer par y mettre 0). Puis il met les valeurs de A et B pour k = 1 dans U. etc...etc... Puis il met les valeurs de A et B pour k = 100 dans U.
Bref, au final, ta variable U est égale à U₁₀₀, et non pas la somme des U de U₀ à U₁₀₀

[Lachimiecphysique]

D’accord merci pour votre réponse, je vais faire quelques recherches sur internet et dans ma tête pour essayer de mieux comprendre le principe d’un algorithme.

[ansset]

...

même pas vu qu'il manquait un "plus".
correction bienvenue.

[Lachimiecphysique]

Bonsoir, juste pour vous dire que je suis toujours en recherche pour l’algorithme du 4)d) , je me permet quand même de vous présenter l’algorithme suivant où S et la somme de U_n pour vous poser une question :

G <— 4949
T<— 7,730662811*10⁴²
S<— G+T

Question: Avons-nous le droit d’utiliser les puissances pour les algorithmes (Sinon quels sont les divers choses interdites dans un algorithme).

Je voudrais savoir également si ma réponse pour la 3) (En déduire que la suite (U_n)est croissante) est correcte ? (Mon raisonnement à l’air trop facile à mon goût...)

La voici :

On sait que Un+1- Un= constante

On connaît Un+1 >= n+3 et Un>= n.
Donc Un+1- Un = n+3-n = 3.

3>0 donc Un+1- Un>0 c’est-à-dire Un+1>Un, (Un) est donc une suite croissante.


Je vous remercie une nouvelle fois pour votre aide, bonne soirée.

[jacknicklaus]

[B]On sait que Un+1- Un= constante

Euh... C'est une plaisanterie ?


Tu as calculé U0 = 0, U1 = 3, U2 = 10
donc U1 - U0 = 3 et U2 - U1 = 7
selon toi, 3 = 7 ???

Tu as même montré que Un = 3ⁿ + n - 1
Donc U(n+1) - Un = 2.3ⁿ + 1. Tu crois que cette expression est une constante ?!!?

Reviens sur Terre. Tu as prouvé que Un >= n. (pour rappel, tu n'as PAS prouvé Un >= n+3, d'ailleurs U0 = 0 qui n'est PAS >= 3.)

est ce que la suite Wn = n est croissante ? Prouve le !
on a Un >= Wn
que dire d'une suite dont les termes sont supérieurs à ceux d'une suite croissante ?

[jacknicklaus]

Bonsoir, juste pour vous dire que je suis toujours en recherche pour l’algorithme du 4)d) , je me permet quand même de vous présenter l’algorithme suivant où S et la somme de U_n pour vous poser une question :

G <— 4949
T<— 7,730662811*10⁴²
S<— G+T

ceci n'est pas l'algorithme demandé. Ce que tu exposes est une addition de 2 valeurs qui sortent de nulle par.

Il faut que tu écrives un algorithme qui calcule, élément par élément, chaque terme UK pour k de 0 à 100 et additionne chacun de ces termes dans une variable qui .... sera la somme demandée.
En gros, un truc du genre :

[à toi de remplacer les ?? par ce qu'il faut]

?? <-- 0

Pour ?? de 0 à 100, répéter les 2 instructions ci dessous
    UK <-- [?? une expression fonction de k, à toi de faire]
    Somme <-- Somme + ??

Afficher Somme

A toi d'adapter en fonction des conventions d'écriture d'algorithme "en langage naturel" que ton prof à exposé en cours.

[Lachimiecphysique]

Bonjour merci pour votre réponse, voici ce que j’ai fais du coup pour la 3)

On sait que U_n >= n .
On nomme la suite (W_n) définie par W_n=n.
Déterminons si la suite (W_n) est croissante :
W_n= n
Alors W_n+1= n+1
Donc W_n+1-W_n= n+1-n = 1
1>0, donc W_n+1> W_n où W_n+1- W_n>0, la suite (W_n) est donc croissante

Donc si U_n>= W_n (ou U_n>=n), alors (U_n) est croissante car cette dernière a des termes supérieurs à la suite (W_n) qui est également croissante.

Cette réponse suffit ? (Merci également pour votre aide à la 4)d) )

Bonne journée

[jacknicklaus]

non ce n'est pas correct. C'est moi qui t'ai induit en erreur hier soir. Une suite supérieure à un suite croissante n'est pas nécessairement croissante. (penser à une suite en dent de scie, mais supérieure à la suite Wn = n)

Il est bien plus simple de prouver directement U_n+1 - U_n > 0 pour toute valeur de n

[ansset]

Il est bien plus simple de prouver directement U_n+1 - U_n > 0 pour toute valeur de n

ben ça, il me semble que c'est demandé dès le début.
le seul truc dans l'algorithme , c'est
- d'initialiser les variables.
-de faire d'itération qui va bien pour passer de la somme de 0 à k à la somme jusqu'à k+1 ( et ce jusqu'à n )

[Lachimiecphysique]

Bonsoir merci pour votre aide, voici ce que j’ai fait:


3) U_n+1-U_n= (3U_n-2n+3)- U_n
= 2 U_n-2n+3

Comment fait-on ensuite pour prouver que 2U_n-2n+3 >0 ? (Faut-il factoriser, développer sachant U_n>=n etc...)

4)d) Voici ce j’ai fait pour l’algorithme:

u<—0
Pour k allant de 0 à 100 répéter les 2 instructions ci-dessous
U_k <— 3^k+k-1 ?? (Comment fait-on pour appliquer une puissance dans un algorithme ?)
Somme <— Somme + Somme


Merci une nouvelle fois, bonne soirée.

[jacknicklaus]

3) U_n+1-U_n= (3U_n-2n+3)- U_n
= 2 U_n-2n+3

Comment fait-on ensuite pour prouver que 2U_n-2n+3 >0 ?

ben, il suffit d'utiliser ce que tu as démontré à la question 2) !
c'est à dire Un >= n. C'est d'ailleurs explicitement dans ton énoncé du 3) : "en déduire que la suite est croissante"

Bien lire les énoncés des exercices est utile

[jacknicklaus]

u<—0
Pour k allant de 0 à 100 répéter les 2 instructions ci-dessous
U_k <— 3^k+k-1 ?? (Comment fait-on pour appliquer une puissance dans un algorithme ?)
Somme <— Somme + Somme

Bon, alors je joue cet algorithme. A toi de me dire si ca fait le résultat attendu. Je fais simplement de K = 0 à K = 3 pour tester
je suis sympa, je corrige ta 1ère erreur qui est de ne pas avoir initialisé Somme à 0

U <- 0
Somme = 0 (tu l'avais oublié)

k = 0 (1er passage dans la boucle)
U₀ <- 3⁰ + 0 - 1 = 0
maintenant U₀ = 0
Somme <- 0 + 0
donc maintenant Somme = 0

k = 1 (2ème passage dans la boucle)
U₁ <- 3¹ + 1 - 1 = 3
maintenant U₁ = 3
Somme <- 0 + 0
donc on a encore Somme = 0

k = 2 (2ème passage dans la boucle)
U₂ <- 3² + 2 - 1 = 10
maintenant U₂ = 10
Somme <- 0 + 0
donc on a encore Somme = 0

k = 3 (3ème et dernier passage dans la boucle)
U₃ <- 3³ + 3 - 1 = 29
maintenant U₃ = 27
Somme <- 0 + 0
donc on a encore Somme = 0


Résultat de ton algorithme : Somme = 0
Euh .... satisfait ???

[Lachimiecphysique]

Bonsoir,

Pour la 3) justement je ne sais pas comment il faut utiliser cette propriété, je m’explique

Première hypothèse : (Prouver que chaque partie est supérieur à 0)

Donc U_n+1 - U_n = 2U_n-2n+3

On sait que U_n >= n pour tout entier naturel n, donc 2U_n>= 2n pour tout entier naturel n, donc 2U_n>0.
Mais ensuite j’ai (-2n +3) à prouver, malheureusement celui-ci est inférieur à 0.

Deuxième hypothèse: (Remplacer U_npar n)

Donc U_n+1-U_n= 2U_n-2n+3.
(Je pense que ceci va vous mettre en colère car ça doit être absurde, je m’excuse d’avance ...)
On sait que U_n>= n , pour moi si U_n est supérieur ou égale à n alors on peut écrire la chose suivante:
U_n+1- U_n= 2*n-2n+3 = 3....

Malheureusement j’hésite entre ces 2 hypothèses, avec la 1ère je ne peux pas justifier et l’autre me paraît absurde car je trouve une constante... Merci si vous pouvez m’indiquer quel chemin prendre.

Sinon pour l’algorithme je ne suis pas vraiment satisfait , je vais voir ce que je peux faire sur les sommes ...

Bonne soirée et encore merci

[jacknicklaus]

On sait que U_n >= n pour tout entier naturel n, donc 2U_n>= 2n pour tout entier naturel n, donc 2U_n>0.
Mais ensuite j’ai (-2n +3) à prouver, malheureusement celui-ci est inférieur à 0.

Une révélation : 2Un - 2n = 2(Un - n).
réfléchis la dessus.

Deuxième hypothèse: (Remplacer U_npar n)

du grand n'importe quoi. je préfère n'avoir rien vu.

[Lachimiecphysique]

Merci,

3) U_n+1 - U_n= 2(U_n-n)+3
*On sait que U_n>= n, donc U_n-n >= 0, alors U_n-n >0
*2>0
*3>0

Donc 2(U_n-n)+3 >0, la suite (U_n) est donc croissante .

C’est correct ?