Transformation continue d'une courbe

[geometrodynamics_of_QFT]

En fait c'est R(q)=-1/q j'avais oublié le signe. Je tire cela du fait que les triangles AOQ et AO(0,R(q)) sont semblables. Et ces triangles sont rectangles, et j'écris des relations de proportionnalité entre leurs cotés de l'angle droit.

Je crois qu'on tient quelquechose!
S'ils sont semblables, pourquoi au bout de la transformation (demi-cercle final) seul le triangle AOQ ne survit??
L'autre (AOC) a été comprimé sur l'axe horizontal!
-----

[invite51d17075]

m'enfin, personne n'a vérifié ma fonction sur un truc comme geoébra ou autre, que je n'ai pas ?

[CM63]

le q est analogue à votre h, c'est juste un autre symbole.
Dans le dessin du tout début, c'est le paramètre variant de 0 à 1 et qui caractérise l'état d'avancement de la transformation...

C'est ça, donc maintenant êtes-vous d'accord avec la relation que j'ai donnée? En fait le rayon du cercle est égal à q+1/q et donc vous devriez pouvoir calculer la longuer de l'arc de cercle en fonction de q (ou de h), c'est égal à (sans filet ) , ok?

[invite57a1e779]

Sur l'axe , le cercle admet deux points diamétralement opposés, A et B, de coordonnées respectives (q,0) et (q',0).

Le cercle passe par le point F de coordonnées (0,1), donc les vecteurs sont orthogonaux (propriété du demi-cercle), c'est à dire :



d'où le rayon du cercle

[CM63]

m'enfin, personne n'a vérifié ma fonction sur un truc comme geoébra ou autre, que je n'ai pas ?

Moi c'est pire je ne sais plus si je l'ai

[invite51d17075]

Je crois qu'on tient quelquechose!
!

ben tenez, tenez,
à quoi ça sert que vieux Ducros se décarcasse.

[geometrodynamics_of_QFT]

ansset, comment savez-vous que la distance est (1-q²)/2q?
Je sais que vous l'aviez écris il y a déjà belle lurette, mais je n'étais toujours pas parvenu à retomber sur l'expression moi-même

[CM63]

Avec mes conventions, si je ne me suis pas trompé le rayon est égal à q+1/q et l'expression de la longueur de l'arc de cercle est donnée par mon message 93 : vérifiez si je ne me suis pas trompé, je dois partir.

[invite51d17075]

Sur l'axe , le cercle admet deux points diamétralement opposés, A et B, de coordonnées respectives (q,0) et (q',0).

Le cercle passe par le point F de coordonnées (0,1), donc les vecteurs sont orthogonaux (propriété du demi-cercle), c'est à dire :



d'où le rayon du cercle

Ha, enfin , OUF !
cela fait longtemps que je le dis , non ?

[invite57a1e779]

Je rappelle mon message #11 du 26 février à 19h40...

Le plus simple : les cercles passant par les deux points de coordonnées (0,1) et (0,-1), ont une équation de la forme:

qui fournit immédiatement l'équation du cercle passant par le point de coordonnées (q,0), puis les coordonnée du centre, la valeur du rayon...
la longueur de l'arc en fonction de l'angle au centre, qui est le double de l'angle inscrit, que l'on connaît si l'on fait une figure...

[geometrodynamics_of_QFT]

Sur l'axe , le cercle admet deux points diamétralement opposés, A et B, de coordonnées respectives (q,0) et (q',0).

Le cercle passe par le point F de coordonnées (0,1), donc les vecteurs sont orthogonaux (propriété du demi-cercle), c'est à dire :



d'où le rayon du cercle

Je ne comprends pas tout :

- parlez-vous de la propriété qu'un diamètre sous-tendu par un point de la circonférence du cercle forme toujours un angle droit?
- comment obtenez-vous qq'+1 pour le produit scalaire?

Et enfin, concernant le rayon, c'est bien la même expression qu'ansset avait formulée il y a un certain temps! (aux signes près)
Je n'ai toujours pas bien compris la preuve...

Mais si l'on part de cette expression, on peut donc maintenant trouver l'expression de la longueur de l'arc en fonction de q??

[invite51d17075]

je ne l'ai jamais contredis,
j'ai juste essayer de trouver une "fonction" f(x) symétrique en 0 ( en partant d'un arc de cercle ) , qui satisfasse les conditions demandées.
il semble que maintenant tout le monde reparte au point de départ.

[geometrodynamics_of_QFT]

Avec mes conventions, si je ne me suis pas trompé le rayon est égal à q+1/q et l'expression de la longueur de l'arc de cercle est donnée par mon message 93 : vérifiez si je ne me suis pas trompé, je dois partir.

ok merci! on vérifie cela! à plus tard.

ansset : on ne part pas du départ : même si l'ont utilise une expression pour le rayon que vous avez donné il y a longtemps, il s'agit maintenant de calculer la longueur de l'arc avec l'expression qu'on a...donc R(q)=1/q

Je m'en vais vérifier l'expression de CM63...qui m'a l'air rigolote : à première vue, elle ne tend pas vers 2 quand q tend vers 0

[geometrodynamics_of_QFT]

Nous en sommes donc là :

Quelle est la longueur de l'arc de cercle d'équation

?

où est le RAYON du cercle.

CM63 a trouvé pour la longueur de l'arc, mais :

- je crois que celle-ci est basée sur l'utilisation de et non l'expression (a priori mais je n'ai toujours pas compris) correcte
- cette longueur ne semble pas converger vers 2 lorsque q tend vers 0...
- cette longueur de vaut pas pi quand q=1 car arcsin 1 ne vaut pas 1/8.

[geometrodynamics_of_QFT]

Je rappelle mon message #11 du 26 février à 19h40...


qui fournit immédiatement l'équation du cercle passant par le point de coordonnées (q,0), puis les coordonnée du centre, la valeur du rayon...
la longueur de l'arc en fonction de l'angle au centre, qui est le double de l'angle inscrit, que l'on connaît si l'on fait une figure...

God's Breath, je ne comprends pas :
quel est le paramètre k?
au point (q,0), l'équation est kq²-k-q=0, que dit-elle? Je ne vois pas...

[geometrodynamics_of_QFT]

God's Breath, on peut réécrire votre équation comme :

.

Cela donne un centre en -1/2k et un rayon de ...est-ce cohérent?

Donc ?? C'est nouveau ou c'était implicite?

[geometrodynamics_of_QFT]

Et surtout que faire de la contrainte supplémentaire que ?
(la position du centre du cercle coïncide dans les 2 formulations, tout comme son rayon ci-dessus)

[invite57a1e779]

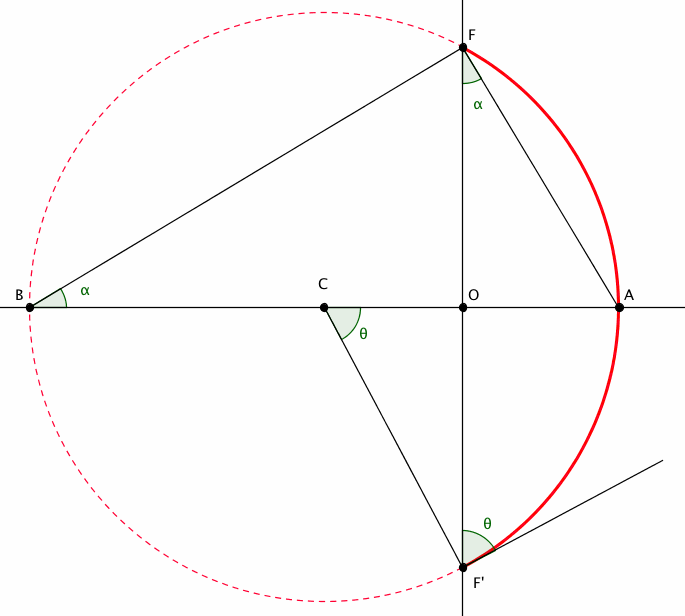
Je charge une figure.

Lorsqu'elle sera visible, je pourrai présenter les calculs correspondants.

[invite57a1e779]

F a pour coordonnées (0,1)
F' a pour coordonnées (0,-1)
A a pour coordonnées (q,0)
B a pour coordonnées (q',0)
C a pour coordonnées (c,0)

L'équation du cercle est de la forme : (faisceau de cercle à points de base déterminé par deux éléments...)

Pour passer par F, cela nécessite : , d'où l'équation :

Le triangle AFB est rectangle en F (inscrit dans un demi-cercle...) donc d'où on déduit successivement :

, , et le rayon du cercle : .

La longueur de l'arc de cercle s'exprime en fonction de l'angle au centre par : et en fonction de l'angle inscrit :

Dans le triangle AOF : , donc:

Dans le triangle COF' : , donc:

Le cercle est d'équation : , équation du second degré en , de discriminant :

.

Comme on travaille sur l'arc F'AF : et , il vaut mieux écrire :

.

L'équation a deux racines (pour ), dont le produit est : , donc les deux racines sont de signes contraires et on veut celle qui est positive, c'est-à-dire la plus grande.

L'arc de cercle est donc donné par : , ce qui n'est pas très sympathique.

Une représentation paramétrique serait certainement bienvenue. On peut par exemple paramétrer le point M de l'arc de cercle par la pente de la droite (BM), ce qui conduit à une représentation par des fractions rationnelles.

[invite51d17075]

décidemment vous n'en voulez pas de mon équation.
courage.

oups , celle de good breath est la même, juste un cgt de coord.

[CM63]

Bonsoir,

Je me suis trompé, l'équation ci-dessous n'est pas bonne:



Car -1/q n'est pas l'ordonnée du centre du cercle mais celle du point diamétralement opposé à (0,q) c'est-à-dire le point le plus bas du cercle.
L'ordonnée du centre du cercle est donc (q-1/q)/2. Et , autre erreur, q+1/q n'est pas le rayon du cercle mais son diamètre. L'équation du cercle est donc:



Ce qui fait, en multipliant par 4:

[geometrodynamics_of_QFT]

décidemment vous n'en voulez pas de mon équation.
courage.

oups , celle de good breath est la même, juste un cgt de coord.

Oui ansset, j'ai dis plusieurs fois que vous aviez donné cette équation plus tôt dans le fil. Sinon de quelle autre équation parlez-vous?



God's breath :
Un tout grand merci pour votre dessin et vos calculs.
Pourquoi obtenez-vous deux expressions différentes pour la longueur de l'arc de cercle?

[invite51d17075]

ecrite au post #27, ça commence à dater mais horizontalement

que l'on un peu simplifier en

[invite57a1e779]

Pourquoi obtenez-vous deux expressions différentes pour la longueur de l'arc de cercle?

Parce que je donne une expression en fonction de l'angle , l'autre en fonction de l'angle .

[CM63]

Ce qui fait:







non?

[geometrodynamics_of_QFT]

Parce que je donne une expression en fonction de l'angle , l'autre en fonction de l'angle .

Oups oui, mal vu...

Mais ces expressions ne tendent pas vers la valeur 2 quand q tend vers 0, elles tendent vers 0...comment concilier cela?

[geometrodynamics_of_QFT]

ansset : ok oui, donc on revient donc bien aux mêmes équations...mais ce petit détour ne m'a pas dérangé en tout cas! désolé encore...

[geometrodynamics_of_QFT]

Ce qui fait:







non?

Je dirais non en vérifiant juste la dernière ligne avec les cas limites q=0 (segment) et q=1 (cercle entré en 0)

[invite51d17075]

Parce que je donne une expression en fonction de l'angle , l'autre en fonction de l'angle .

oui, tu as raison,
j'ai fait pareil pour vérifier la longueur.
deux approches en en prenant une autre quand h ( ou q ) était petit
par contre je ne regarde plus vos calculs, les miens sont terminés.

[invite57a1e779]

Une erreur de copié-collé a fourni une valeur erronée du rayon du cercle, et s'est propagée à la longueur de l'arc.

Les valeur exactes sont : et .