Transformation continue d'une courbe

[geometrodynamics_of_QFT]

Bonjour,

Je me pose une question concernant une transformation qu'il est beaucoup plus facile de décrire par un petit dessin :


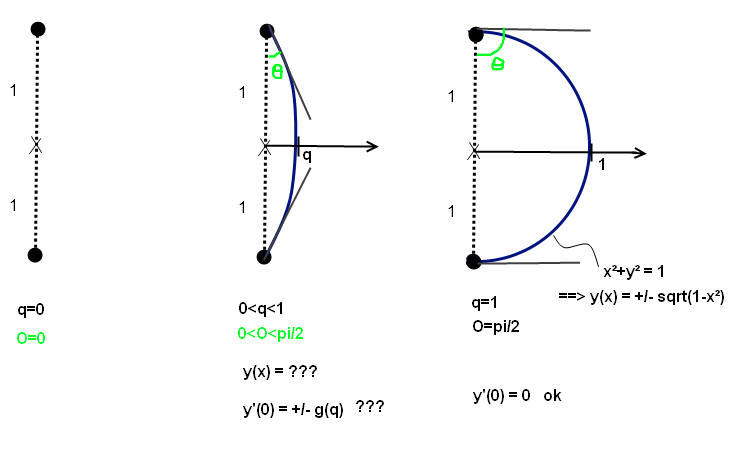
Rapidement, on part d'un segment de droite (que l'on peut imaginer "élastique" pour appréhender la situation naturellement) de longueur 2.
C'est l'état initial, et on désire aboutir à l'état final qui consiste à ce que ce segment de droite épouse un demi-cercle de rayon 1. (Sa longueur aura donc été multipliée par un facteur pi/2 au cours de la transformation)

Donc de manière plus complète, on part d'un segment, on l'étire des deux-côté (pas d'un seul comme sur mon dessin) en formant une sorte d'amande, pour arriver jusqu'au cercle final.

Ma question est :
Quelle est la forme analytique de la courbe dans un des état intermédiaire, caractérisé par exemple par l'abscisse q du point où la courbe croise l'axe horizontal?
J'ai toruvé des infos pour les dérivées aux deux points d'attache, qui doivent varier continûment entre l'infini et 0 lorsqu'on passe de x=0 à x=1??
Mais puisque la fonction finale est une quadrique (le demi-cercle)...comment vérifier ces conditions?
La courbe intermédiaire n'est pas un bout d'ellipse (les dérivées sont non nulles aux points d'attache)

En bref, je ne parviens pas à trouver l'expression de la courbe intermédiaire....

Je vous remercie infiniment pour votre aide!
Bien à vous
-----

[geometrodynamics_of_QFT]

Je reprécise pour la clarté qu'il y a donc un axe privilégié dans la transformation, dans ce cas l'axe vertical.

- la courbe est toujours localement perpendiculaire à l'axe horizontal au cours de la transformation, au point où elle le croise ;
- la courbe passe continument entre être localement parallèle à l'axe vertical jusqu'à être perpendiculaire à l'axe vertical au cours de la transformation, aux points d'attache.

Ce sont des sortes de contraintes du problème que je considère.

En bref, je ne parviens pas à trouver l'expression de la courbe intermédiaire de telle manière qu'en faisant varier continûment un de ses paramètres entre 0 et 1, on passe d'un segment à un demi-cercle.

[geometrodynamics_of_QFT]

S'agit-il d'une spline dont les coefficients cubiques s'annulent pour l'état final?

[Médiat]

Bonjour,

Un arc d'ellipse dont l'excentricité varie, il "suffit" de choisir une représentation paramétrique dépendant d'un paramètre entre 0 et 1 par exemple.

[A voir en vidéo sur Futura]

[invite57a1e779]

Bonjour,

On peut aussi prendre considérer que l'on a en permanence un arc de cercle, dont le centre vient "de l'infini" pour se finir sa course au milieu des extrémités immobiles de l'arc.

[CM63]

Bonjour,

Je prendrais tout simplement deux arcs de cercles. Au départ ils sont confondus et ont un rayon infini (une courbure nulle) : c'est le segment (0,-1) (0,1). Oups!!!

[geometrodynamics_of_QFT]

Bonjour,

On peut aussi prendre considérer que l'on a en permanence un arc de cercle, dont le centre vient "de l'infini" pour se finir sa course au milieu des extrémités immobiles de l'arc.

Merci, oui je vois bien ce que vous voulez dire.

Mais dans ce cas, si le centre est en (moins) l'infini et qu'on y fait correspondre le parametre q=0, et le cercle final en q=1, comment passe-t-on continûment d'un rayon infini en q=0 à un rayon fini en 0<q<<1?
Quel est le rayon R(q) de ce cercle pour un q donné entre 0 e t 1? (avec R(q=1)=1)

[geometrodynamics_of_QFT]

R(q) = 1/q remplit ces conditions, mais pourquoi pas 1/q² ou 1/q^18?

[invite57a1e779]

Soit l'abscisse du centre du cercle (l'ordonnée est nulle), on veut obtenir:



Il suffit de prendre:

ou :

si l'on veut des calculs rationnels.

Le rayon du cercle est dans tous les cas : .

[CM63]

Bonjour,

Je ne vais faire qu'une partie du raisonnement car je dois partir: l'équation du cercle est : , il n'y a pas de terme en car le centre du cercle est sur l'axe des x. On peut donc exprimer y en fonction de x(avec + et -) . L'abscisse du centre est alors égale à a. Désolé je dois partir.

A plus.

[invite57a1e779]

En fait, dans mon dernier message, il y a confusion : j'ai pris pour un paramètre variant de 0 à 1, mais ce paramètre n'est pas forcément l'abscisse du milieu de l'arc de cercle...

Le plus simple : les cercles passant par les deux points de coordonnées (0,1) et (0,-1), ont une équation de la forme:



et il suffit de déterminer k pour que le cercle passe par le point de coordonnées (q,0).

La valeur k=0 correspond au segment initial, le cercle étant alors dégénéré en une droite.

[geometrodynamics_of_QFT]

Merci pour vos réponses à tous les deux.

Je vais donc combiner les deux méthodes pour vérifier la forme de omega....et essayer de l'exprimer en fonction de a...
Car elle doit forcément être unique cette forme j'imagine??!!
Je ne comprends pas qu'on puisse avoir le choix de choisir entre un logarithme et une expression rationnelle...
Merci.

[geometrodynamics_of_QFT]

J'ai envie de ovir cela comme une sorte de transition de phase :

pour une longueur de segment initiale nulle, on a une transition du premier ordre en quelque sorte, tandis que pour une longueur de segment initiale finie, le passage du cercle dégénéré à un arc de cercle serait une transition du second ordre...
Enfin ce n'est qu'une vision imagée...
Mais quelque chose me turlupine dans ce problème, j'ai l'impression que c'est lié à un espace à géométrie hyperbolique...l'infini est à une distance finie (q=0)...Je vais chipoter avec tout ça...

Car comme le segment mesure 2 unités, le moindre arc de cercle, aussi grand soit-il, qui passe par ces 2 points a (forcément) son centre à une distance finie...
Ce n'est pas comme si on partait de deux points infinitésimalement proche l'un de l'autre : ici les deux points d'attache sont à une distance finie dès le début lorsque q est "encore" infinitésimal!

[invite57a1e779]

Voir le message #11...

[Tryss2]

En bref, je ne parviens pas à trouver l'expression de la courbe intermédiaire....

Il existe une infinité de façons de passer de la première à la dernière courbe. Si tu ne spécifie pas un plus, tu as l'embarras du choix

[geometrodynamics_of_QFT]

Bonjour,

Il existe une infinité de façons de passer de la première à la dernière courbe. Si tu ne spécifie pas un plus, tu as l'embarras du choix

C'est notament sur cet aspect-là que j'aimerais que s'oriente la discussion autour de ce problème qui se déroule ici, si cela est possible...

Car en effet dès le début de la discussion, l'un a mentionné un arc d'ellipse dont l'eccentricité varie le long du trajet, et un autre un arc de cercle dont le rayon diminue le long du trajet....

Je conçois donc qu'il y ait une infinité de solutions si on n'introduit pas de contrainte supplémentaire, et c'est un problème qui est perturbant
Quelle serait une contrainte naturelle qui briserait le moins de symmétries et rendrait la solution unique?

Je pense qu'une autre façon de poser la question serait : "Quelles sont les expression algébriques qui tendent vers un cercle lorsqu'un de ses paramètres (autre que les variables quadratiques) varie continûment (entre par exemple 0 et 1)". Est-ce correct?

Je vous remercie pour toute remarque, suggestion, idée, précision, réponse, etc..merci beaucoup.

[ansset]

Je pense qu'une autre façon de poser la question serait : "Quelles sont les expression algébriques qui tendent vers un cercle lorsqu'un de ses paramètres (autre que les variables quadratiques) varie continûment (entre par exemple 0 et 1)". Est-ce correct?
.

je propose deux critères, par exemple ( on peut en prendre d'autres )
que l'équation soit quadratique , et que la longueur soit minimale.

ou un autre unique :
que la courbe intermédiaire soit un arc de cercle passant par les 3 points..

[CM63]

Bonsoir,

Mille excuses je vais encore être approximatif car je ne reste pas longtemps. Dans l'équation du cercle que nous avons donnée, l'abscisse du centre varie entre - l'infini et 0 (demi-cercle de droite). Il suffit peut-être de faire un changement de variable pour obtenir un paramètre qui varie entre 0 et 1?

[ansset]

dans le second cas , on peut choisir la vitesse d'évolution en posant que la vitesse de hauteur la courbe soit linéaire
avec H(0)=0 et H(1)=1
( une petite singularité en 0 quand même )

[geometrodynamics_of_QFT]

je propose deux critères, par exemple ( on peut en prendre d'autres )
que l'équation soit quadratique , et que la longueur soit minimale.

ou un autre unique :
que la courbe intermédiaire soit un arc de cercle passant par les 3 points..

Merci beaucoup.
Je continue à réfléchir tout haut en rebondissant sur vos propos:

-Si l'on impose que l'équation soit quadratique et que la longueur soit minimale, l'arc de cercle final doit aussi avoir sa longueur minimisée, mais par rapport à quoi? Uniquement sur base du fait que la courbe doit passer par 3 points (2 points d'attache et le point (q,0))?

-si la courbe intermédiaire est un arc de cercle, ce que je comprends pas est que lorsque le paramètre q est infinitésimal q>0, le rayon de courbure est fini. Il n'est infini que pour q=0 exactement (car le segment initial a une longueur finie et non nulle). Comment se produit la transition infini-> fini lorsque q passe de 0 à espilon>0?

[geometrodynamics_of_QFT]

dans le second cas , on peut choisir la vitesse d'évolution en posant que la vitesse de hauteur la courbe soit linéaire
avec H(0)=0 et H(1)=1
( une petite singularité en 0 quand même )

Oui merci exactement, comme si l'on assimilait q à t, entre 0 et 1 unité de temps (le temps s'écoule linéairement).
Ca me rassure d'arriver à raccroches mes bribes d'idées à vos remarques.

Concernant celle-ci, est-ce que contraindre la vitesse aboutit à une forme algébrique différente pour la courbe?

Quel est le type de singularité qui se produit en 0? Dans quels autres domaines des mathématiques ce type de singularité se produit-il?

CM63 : Merci. Oui j'imagine que l'on peut chosir le paramètre arbitraire que l'on veut, du moment qu'il varie de manière continue durant la transformation, et qu'il existe des transformations pour passer de l'un à l'autre.

Concernant ma réflexion plus générale, je réfléchis autour du problème des dimensions, comme ici passer continûment de la 1D (segment) à la 2D (cercle).
Le même type d'opération peut être imaginée pour passer du - disque cette fois-ci - à la sphère en "étirant des 2 côtés du disque une matière plastique type ballon gonflable en constraignant sa forme de manière à aboutir à 2 hemisphères de chaque côté", càd faire la même opération qu'actuellement, mais avec une dimension spatiale en +.

Bref, je me pose ces questions en étudiant de loin les fractales, ensembles de Mandelbrot etc en hobby.
C'est alors que je me suis retrouvé à me questionner sur des possibilités de passer de manière continue d'un certain nombre entier de dimensions à un autre...
Mais il est certain que la singularité en question en x=0 coïncide avec la transition 1D-2D...

En espérant que cela puisse vous guider à me diriger vers les sujets traitant de ces questions et en lien avec ce domaine.
Merci, bien à vous!

[geometrodynamics_of_QFT]

la singularité en 0 n'a-t-elle pas aussi un lien avec le fait que l'on passe d'un segment de longueur entière, à un arc de cercle de longueur irrationnelle (et transcendentale)? (puisqu'au cours de la transformation, on passe d'une longueur de 2 à une longueur de Pi)

Une nouvelle contrainte aussi pourrait être que la déformation élastique (si l'on assimile la courbe à un ruban élastique) soit linéaire au cours de la transformation? Qu'en dites-vous?
Dans ce cas-là, peut-être que la hauteur q(t) ne se déplacerait pas à vitesse constante??

Il y a-t-il un lien avec la géométrie hyperbolique?

[geometrodynamics_of_QFT]

Je pense ici à une analogie avec le dessin d'Escher des anges et diables.

Au centre (en r=0), le cercle de rayon 1, et en la coordonnées radiale "euclidienne" r=1, le segment (ou cercle de rayon infini), dont nous parlons.

Or il se trouve que cette zone frontière est chaotique juste à l'intérieur de la circonférence, ou fractale...Donc de dimension fractionnaire...un état entre 2 dimensions entières, comme le passage de q=0 à q>0 dans la problématique de départ...
Je trouve tout cela très intéressant et j'ai envie de découvrir les liens qu'il existe entre toutes ces choses...

[geometrodynamics_of_QFT]

Tout dernier message avant d'attendre les feedback :

Si l'on considère le cas où la courbe est un arc de cercle dont le centre part de -l'infini et arrive à 0.
Imaginons que l'on veuille faire la transformation inverse, donc simplement partir de l'état où la courbe est le demi-cercle unité et arriver au segment. Comme partir du centre du dessin de Herschel et arriver au bord.
Si l'on impose par exemple que la tangeante de la courbe aux 2 points d'attache varie linéairement entre 0 et pi/2 (donc de manière uniforme), alors:

On ne pourra jamais observer une simulation de la transformation : le point O du centre du cercle va accélérer dans la direction -x, il va dépasser la vitesse de la lumière (lol), dépasser la vitesse de 1 nombre de Graham de km/s sans jamais arrêter d'accélérer (car il n'atteindra jamais -l'infini..du moins pas dans une géométrie euclidienne à mon sens)...

Est-ce moi qui délire, ou bien quelque chose de particulier se passe inaperçu lorsque la tangeante tourne d'un quart de tour?
Pendant ce temps-là, un centre de cercle revient de l'infini et arrive en 0...en un temps fini!

[ansset]

pour info avec le cercle.
l'équation toute simple de la distance du centre du centre en fonction de la hauteur h de la courbe est:
y=(1-h²)/h
on peut écrire h=t/k pour avoir une montée continue en une durée k
avec donc une singularité en h=0 si on part du segment pour aller vers le demi cercle ( h=1 et y=0 )
on peut inverser évidemment l'équation en fct du temps h=1-t/k
et la singularité se retrouve en t=k.

ça doit marcher avec les b-splines, mais je n'ai plus les équations en tête ( shame on me ! )

[minushabens]

On ne pourra jamais observer une simulation de la transformation : le point O du centre du cercle va accélérer dans la direction -x, il va dépasser la vitesse de la lumière (lol), dépasser la vitesse de 1 nombre de Graham de km/s sans jamais arrêter d'accélérer (car il n'atteindra jamais -l'infini..du moins pas dans une géométrie euclidienne à mon sens)...

dans le problème tel que tu le posais il n'y avait pas de notion de vitesse, mais si tu veux préciser que la tangente tourne à vitesse angulaire constante alors oui, le centre du cercle se déplace à une vitesse qui tend vers l'infini, mais ce n'est nullement un problème: la géométrie ne connaît pas les limitations de la physique.

Est-ce moi qui délire, ou bien quelque chose de particulier se passe inaperçu lorsque la tangeante tourne d'un quart de tour?
Pendant ce temps-là, un centre de cercle revient de l'infini et arrive en 0...en un temps fini!

si tu aimes te référer à une situation physique, tu peux imaginer une lampe éclairant un mur infini. Si la lampe tourne le point éclairé se déplace sur le mur et si la lampe finit par éclairer parallèlement au mur, le point éclairé s'est déplacé "vers l'infini" à une vitesse croissante (sauf que dans la réalité les murs infinis n'existent pas).

[ansset]

pour info avec le cercle.
l'équation toute simple de la distance du centre du centre en fonction de la hauteur h de la courbe est:
y=(1-h²)/h

j'ai dit 2 bétises.
déjà c'est :
y=(1-h²)/(2h) faute de frappe.
mais la singularité est celle de la distance du centre à la droite que j'ai appelé y à tord.
si on parle de la fonction f(x) centrée en 0 et qui satisfasse les conditions
en reprenant l'équation du cercle.
je vous passe les petits calculs.
la fonction est


et quand h->0
la fonction converge de manière uniforme vers 0 sur l'intervalle [-1;1]

et pour les tangentes en -1 et 1

[Médiat]

Bonjour,

Une solution très simple :

X = rsin(t)
Y = cos(t)

pour 0 <= t <= pi

et 0 <= r <= 1

[ansset]

cela ne satisfait pas l'évolution entre 0 et l'inf des tangentes aux extrémités.

[ansset]

dans ma fonction , j'ai bien sur remis la courbe à l'horizontal.