Somme vectorielle

[azizovsky]

Donc pour terminer le raisonnement:



et

...

Un erreur quelque part??

-----

[geometrodynamics_of_QFT]

Justement :



jusque là t'es d'accord? (ce sont les 3 premiers termes n=0, n=1 et n=2) )
je poursuis:



toujours d'accord ?
on continue :



et enfin :



est-ce qu'on est d'accord?

[geometrodynamics_of_QFT]

RECAPITULATIF POUR ET L=2
============================== ======

Soit le point de convergence, fonction de , défini par:



où

• ,
  
• ,
  
• 
  
• et et .

Alors pour , on a:



et



Donc



et


où



Est-ce que pour l'amour du ciel, quelqu'un pourrait confirmer ces résultats s'il vous plait? Azinovski? God's brearth? Mediat? ggo? ansset?

[azizovsky]

j'en ai que ça à ma disposition:

[geometrodynamics_of_QFT]

j'en ai que ça à ma disposition:

ici, ce sont des puissances de 2 aux dénominateurs...comment faire?



donc ? noon, si proche de et pourtant si loin

[geometrodynamics_of_QFT]

ici, ce sont des puissances de 2 aux dénominateurs...

et non des dénominateurs à la puissance 2...

[azizovsky]

la condition est : càd

[geometrodynamics_of_QFT]

la condition est : càd

Salut,



pour moi c'est faux : en , , donc comme on le devine ci-dessous :


On est d'accord?

[azizovsky]

on'a : avec la condition:

converge, soyez le bien venu dans l'espace de Hilbert.

[geometrodynamics_of_QFT]

azizovsky,

je capte pas.
Pourtant je sens qu'il y a un lien, mais je capte pas ce qu'est ton S et on A...

car un autre truc :
...

on est ok sur ça?

[azizovsky]

azizovsky,

je capte pas.
Pourtant je sens qu'il y a un lien, mais je capte pas ce qu'est ton S...

car un autre truc :
...

on est ok sur ça?

on'ai au croisement de plusieurs domaines du maths, donc.....

on ' quantifié le support ( ensemble de ses points) de certaines courbes....

[geometrodynamics_of_QFT]

============================== ==============
On peut écrire que :


car, si alors

Donc et
Et, en particulier, pour , ça donne et

============================== ==============

autre méthode, même résultat : ok?

[azizovsky]

Ma méthode ad hoc pour est la suivante :












.............................. .............................. ........................







.......

[azizovsky]

[QUOTE=azizovsky;5522267] rectification :

[geometrodynamics_of_QFT]

haha excellent!

mais comme on voit que expérimentalement (le vecteur (1,2), pas le scalaire 6/5)

tu peux continuer

par


....

non?

le passage de la ligne 2 à la ligne 3 étant prouvé dans mon post #62

[azizovsky]

la dernière équation, je ne sais pas car j'ai mélangé les coordonnées avec la longueur de la 'courbe' qui est de L=2.

[azizovsky]

tu peux la mettre sous forme:

, avec

[geometrodynamics_of_QFT]

oui donc pour que les choses soient bien claires lol

N'est PAS un "trajet" anguleux qui suit les vecteurs, et sa norme n'est pas la longueur du parcours, donc la somme des longueurs des semgents.
Donc non, on est bien d'accord

est un vecteur allant de l'origine au point de convergence, et sa norme n'a rien de particulier, si ce n'est qu'elle est proportionnelle à en .

Mais je propose qu'on commence, en parallèle à cette discussion autours de cette valeur particulière de la construction (n'oublions pas son origine), une discussion sur le comportement général de pour , obtenir le lieu pour le domaine de variation de cet angle, et dans une formulation qui permette d'étudier son comportement pour des valeurs de , et imposer la continuité avec le cas particulier dont nous continuons la discussion.

Car on n'a pas isolé ce paramètre pour rien, exploitons maintenant notre formulation puissante valable pour n'importe quel !!
Je suis certain que nous découvrirons de nombreuses surprises

[geometrodynamics_of_QFT]

tu peux la mettre sous forme:

, avec

Yep ok, donc ça je vois bien maintenant! Le lien est clair nikel...

et donc, c'est bien ça? (avec un facteur 2 qui traîne j'sais pas où)

[geometrodynamics_of_QFT]

la dernière équation, je ne sais pas car j'ai mélangé les coordonnées avec la longueur de la 'courbe' qui est de L=2.

Ok pour la longueur=2, et celle-ci est constante et ne dépend pas de ...

En fait , si je ne me trompe...

[geometrodynamics_of_QFT]

donc PAS ok avec L=2 lol, le segment 0 a déjà une longueur de 2 ^^

L = 2+1+1/2+1/4+.... = 3+2/3=11/3?

[azizovsky]

donc PAS ok avec L=2 lol, le segment 0 a déjà une longueur de 2 ^^

L = 2+1+1/2+1/4+.... = 3+2/3=11/3?

la longueur est: fixe( invariant de geometrodynamics_of_QFT ) maintenant un problème:

comment varie le point limite de la 'courbe' avec l'angle ???

[geometrodynamics_of_QFT]

la longueur est: fixe( invariant de geometrodynamics_of_QFT ) maintenant un problème:

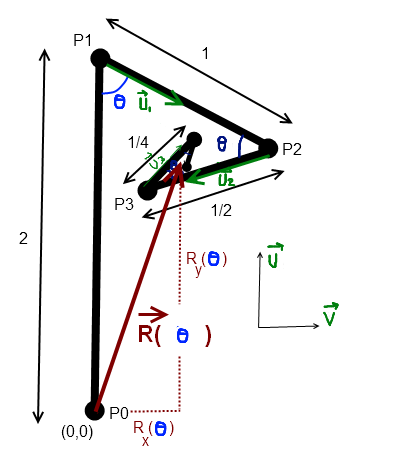
Je me base simplement sur l'illustration lol: (et je suis vraiment taré si je me plante sur ce coup )

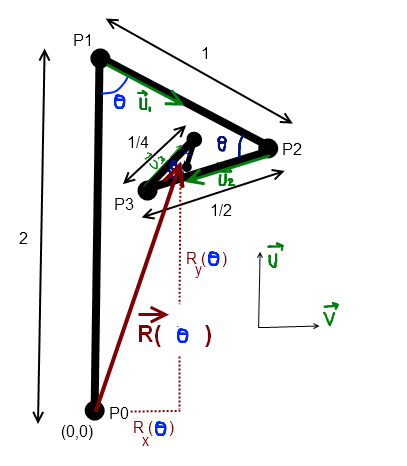
Pour moi, la longueur est si ton résultat est juste.
2*2 vis-à-vis de la factorisation d'un 2 par rapport à ta longueur,
et 2+2 car on ajoute simplement un segment de longueur 2 à ce que tu pensais.

comment varie le point limite de la 'courbe' avec l'angle ???

That's the question!

Mais je propose qu'on commence, en parallèle à cette discussion (...) , une discussion sur le comportement général de pour , obtenir le lieu pour le domaine de variation de cet angle (...)

Je m'y atèle et je compte sur ta participation :-p

[azizovsky]

tous dépend de la longueur initiale (l'invariant qui est donné d'avance) de la corde , si tu prend ou ou comme variable qu'on fixe d'avance pour l'instant .

[geometrodynamics_of_QFT]

RECAPITULATIF
==========

Soit le point de convergence, fonction de , défini par:



où

• ,
  
• ,
  
• , . (homothétie...)

============================== =======================
a) pour et

où

============================== =======================
b) pour

On construit (comme dit plus haut...)


Mais si (càd ) alors



Donc
et

et pour et , ça donne et

y'a un facteur 2 quelque part, le jeu est de le trouver...mais sinon c'est cohérent?

============================== =================
avec 'ta notation' Azivoski, on aurait un truc du genre:



où , , etc...truc du genre? dans l'idée?

[geometrodynamics_of_QFT]

pas de singularité en ? wtf?

[geometrodynamics_of_QFT]

On se disperse...
Il faut repenser à la construction initiale et à la singularité:
les centres de cercles émanant des extrémités des segments, et sur la médiatrice de ceux-ci, passent d'une distance finie à une distance infinie quand passe de à
Or, l'arc défini par deux rayons, et définissant le segment en question, garde une longueur finie en passant la singularité!
J'y vois un ajustement fin menant au point de convergence fini...

good night!

[geometrodynamics_of_QFT]

on peut en tout cas toujours s'amuser à voir ce que ça donne pour le nombre d'or lol, les coudes des segments correspondraient aux intersections des coins des carrés sur ton dessin de spirale d'or, et le et pour sont peut-être une invitation pour nous attirer dans ce coin-là...mais bon...LOL c'est un peu faire joujou à l'aveuglette haha

[geometrodynamics_of_QFT]

Y'a pourtant bien un truc à aller chercher...

les analogies sont si nombreuses (oscillateur harmonique, etc...), le problème est si trivial : des 2, des cos+sin..fin je veux dire que du classique quoi, c'est pas une expression tordue, c'est même plutôt un cas d'école, bien pur, éminament simple.
Il se cache forcément quelque chose, il faut continuer à chercher. Il faut fouiller ce bras articulé de fond en comble.

[azizovsky]

Bonjour, on va utiliser la méthode du simple au générale, soit qu'on a que un point dans le premier cercle :

avec et après on va faire pour tous

on va faire éclater cette expression:

pour un deuxième observateur au bout du segment, lui aussi, il a dans sont référentiel un point qui va bougé à la même vitesse angulaire au bout du segment de rayon

avec :



on'a

un 3 ème observateur au bout du segment du deuxième.....

avec toujours



.....n changement de référentiels, c'est le matin, après