
- Forum
- Futura-Sciences : les forums de la science
- MATHEMATIQUES
- Mathématiques du supérieur
- Somme vectorielle
Somme vectorielle
- 02/03/2016, 23h21 #31azizovsky
- Date d'inscription
- septembre 2010
- Messages
- 5 348
Re : Somme vectorielle
------
Dernière modification par azizovsky ; 02/03/2016 à 23h24.

- 02/03/2016, 23h48 #32invite57a1e779
- Date d'inscription
- janvier 1970
- Messages
- 9 645
Re : Somme vectorielle
Je donne des éléments de réponse à ce message
Les notations étant par trop horribles, je modifie :
 en
en 
 en
en 
 en
en 
 en
en 
 en
en  .
.
Les expressions

deviennent

J'exprime et
et  en fonction de
en fonction de  et
et  sous la forme
sous la forme

La formule est satisfaite pour avec :
avec :  .
.
Si elle est satisfaite au rang , alors
, alors

donc elle est satisfaite au rang avec :
avec :  , c'est-à-dire que
, c'est-à-dire que  est la somme partielle de la série de terme général
est la somme partielle de la série de terme général  :
:

et je souhaite bon courage à ceux qui veulent essayer de s'attaquer à la série


- 03/03/2016, 00h35 #33geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
Mille merci God's breath!
Je ne m'attendais plus à un si beau geste de votre part, je vous en remercie majestueusement.
adoptons vos notations en effet un peu plus claires...
J'ai tout compris, jusqu'à l'avant dernière ligne.
- Tout d'abord, je suppose que vous vouliez écire :

et non
Ce qui fournit donc

et non
- A partir de là, je ne comprends pas bien la construction et la déduction de la "somme partielle", mais je vois qu'elle semble liée à la formulation matricielle que j'avais entreprise, où pour rappel j'avais obtenu dans votre notation:

où
 et
et 
- Je cherche donc à relier cela (si c'est juste) à votre formulation par somme partielle.
Mais ayant reformulé votre comme ci-dessus, je ne comprends pas bien comment vous obtenez
comme ci-dessus, je ne comprends pas bien comment vous obtenez
edit :
Encore merci pour votre soutien!
A bientôtDernière modification par geometrodynamics_of_QFT ; 03/03/2016 à 00h38.

- 03/03/2016, 00h41 #34geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
Donc ben tout est clair finalement...sauf qu'il reste à vérifier :
-si les deux formulations sont équivalentes;
-si la relation de récursion pour les tangentes est bien celle-là sur base de la construction géométrique considérée au départ;
-s'il n'y a pas d'autres méthodes pour résoudre analytiquement cette somme...
bref, y'a du boulot
Dernière modification par geometrodynamics_of_QFT ; 03/03/2016 à 00h43.

- 03/03/2016, 01h16 #35geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
Wopopop!!!
J'ai du nouveau:
- Ecrivons-donc le vecteur final qu'on veut obtenir.
En utilisant

On a

La première ligne via ma formulation, et la seconde via la vôtre, God breath.
où
 (à vérifier car je ne suis pas sûr)
(à vérifier car je ne suis pas sûr)
et

N'existe-t-il pas un moyen pour relier ces équations? Et ainsi obtenir une autre méthode que la somme des ?
?
Vous avez une double somme, j'ai une somme et un produit...
Dernière modification par geometrodynamics_of_QFT ; 03/03/2016 à 01h20.

- 03/03/2016, 01h32 #36geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
Car si on reprend l'autre écriture (du post 3, le jeu avec les asin(tan x) etc) :
 où
où

et
 ,
,
la matrice M n'est plus vraiment une matrice de rotation classique, dans le sens où ...si?
...si?
PS : dans mon post précédent, la seule raison pour laquelle je garde l'expression (n+1-k) est parce qu'on ne peut pas inverser l'ordre de la multiplication, donc je ne peux pas simplement écrire .
.
Dernière modification par geometrodynamics_of_QFT ; 03/03/2016 à 01h36.

- 03/03/2016, 02h00 #37geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
dernier truc:
petit interlude pour éviter la propagation des erreurs : (car si ça tombe on calcule pour rien, OU l'expression correcte sera plus facile à manipuler, qu'en sait-on!)
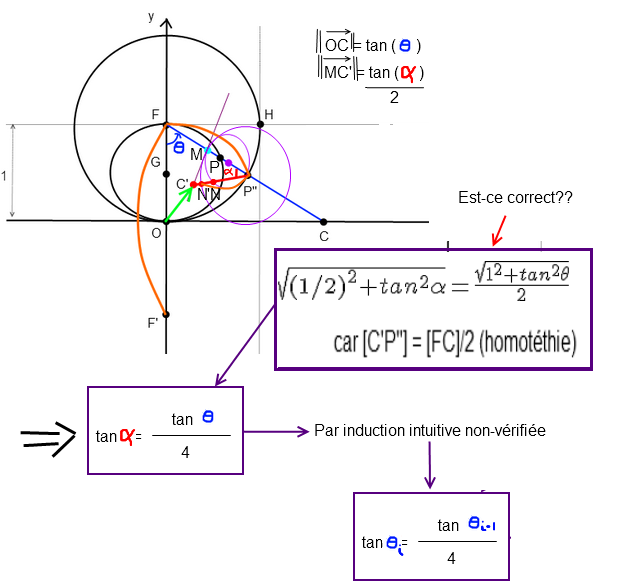
quid pour la relation de récursion des angles?
PS : les petits cercles (le noir centré en G et le mauve centré au point mauve) sont inutiles, vous pouvez en faire abstraction.Dernière modification par geometrodynamics_of_QFT ; 03/03/2016 à 02h02.

- 03/03/2016, 15h51 #38geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
Aaaaaand..that's a fail!
En effet, après vérification, la relation de récurence correcte pour les angles est : et non
et non 
Donc partout où il y a des 4, on les remplace par , de manière à ce que tous les résultats restent corrects.
, de manière à ce que tous les résultats restent corrects.
Et maintenant, c'est comme si on venait de découvrir que , mais peu importe, on peut même continuer avec
, mais peu importe, on peut même continuer avec  arbitraire si on veut généraliser...et pouvoir l'utiliser un jour comme variable... (vu qu'il s'agit du rapport d'homotétie des longueurs et des tangentes)
arbitraire si on veut généraliser...et pouvoir l'utiliser un jour comme variable... (vu qu'il s'agit du rapport d'homotétie des longueurs et des tangentes)
J'arrive avec quelques nouveaux résultats...Dernière modification par geometrodynamics_of_QFT ; 03/03/2016 à 15h55.

- 03/03/2016, 20h08 #39geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
============================== =======================
POST CHECK_POINT
Reformulation claire et self-contained du problème dans l'état actuel d'avancement
============================== =======================
On cherche les composantes du vecteur :

où et
et 
 pour
pour  ,
,  ,
, 

 .
.
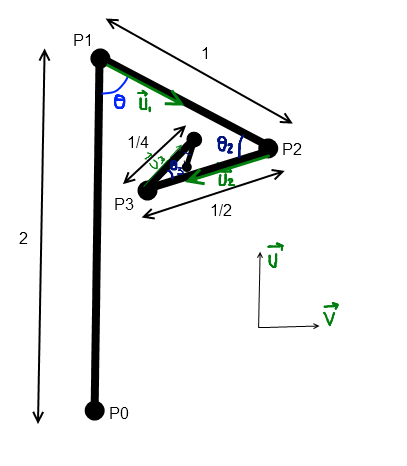
============================== =======================
- [#39.a]
Si les deux formulations (2ème ligne et 3ème ligne) sont correctes, alors on doit avoir en effectuant le produit des matrices M:

Or,

J'imagine que cela provient du fait que j'ai sorti de la somme, à cause de son insertion dans le produit de matrice impossible?
de la somme, à cause de son insertion dans le produit de matrice impossible?
Si je ne me trompe pas, God's breath a démontré par induction que
Donc pour boucler la boucle:
 Correct?
Correct?
- [#39.b]
Puisque et que
et que  et
et 
On a

où
 et
et 
et

Voilà ma question : Il y a-t-il de l'avenir dans la méthode ci-dessous? (qui est lourde, donc je le demande avant)
On voit que l'élément (1,1) du produit des matrices
des matrices  contiendra un terme
contiendra un terme 
Et on observe aussi que et
et  .
.
Donc on voit que

Pourrait-on, pour les 4 catégories de termes (AA, BB, AB, BA) intervenant dans le produit, essayer de "factoriser" des éléments définis par récursion, de la même manière qu'avec les tangentes des angles?
Dernière modification par geometrodynamics_of_QFT ; 03/03/2016 à 20h13.

- 03/03/2016, 20h39 #40azizovsky
- Date d'inscription
- septembre 2010
- Messages
- 5 348
Re : Somme vectorielle
Bonsoir, une représentation pour avoir
 :
:
on pose qu'on peut transformer pour simplifier:
qu'on peut transformer pour simplifier:
 avec
avec  avec x>0
avec x>0
 avec
avec 
.............................. ...................
 avec
avec 
.............................. ...................
 avec
avec 

c'est lourd pour l'écriture, mais une idée....Dernière modification par azizovsky ; 03/03/2016 à 20h41.

- 03/03/2016, 21h15 #41geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
Salut azizovsky,
je viens d'apprendre une terrible nouvelle juste avant de lire ton message.
Mais je le garde dans un coin car ça peu en effet s'avérer utile! tout ce qui peu transformer des produits en sommes ici sera d'un grand secours.
Mais voilà...
La nouvelle est en même temps dramatique et joyeuse, en même temps bonne et mauvaise:
J'ai revérifié les relations de récurences pour les angles sur base de la construction géométrique et...
Tous les angles sont égaux!!!! !!!!
!!!! 
donc c'est BAD car tous les calculs sont faux,
mais c'est COOOOL car ça simplifie TOUT
back form scratch, update coming...
PS : Quand j'vous dit de vérifier ems calculs...j'lai demandé 100x de vérifier la récurence des angles...Dernière modification par geometrodynamics_of_QFT ; 03/03/2016 à 21h20.

- 03/03/2016, 21h24 #42azizovsky
- Date d'inscription
- septembre 2010
- Messages
- 5 348
Re : Somme vectorielle
Ce n'est pas grave, un peu de sport cognitif pour l'entretient des neurones de temps en temps .(les miens sont bouché par la colle ...)
.(les miens sont bouché par la colle ...)
Dernière modification par azizovsky ; 03/03/2016 à 21h27.

- 03/03/2016, 21h25 #43geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
Azizovki, premier qui trouve
 a gagné.
a gagné.
le seul truc qui change par rapport au post #39, c'est que , et ça simplifie de dingue...
, et ça simplifie de dingue...
c'est parti!
- 03/03/2016, 21h37 #44azizovsky
- Date d'inscription
- septembre 2010
- Messages
- 5 348
Re : Somme vectorielle
sans trop réfléchir les vecteurs sous forme
 avec
avec  dans le plan de Gauss ???(je suis saturé)
dans le plan de Gauss ???(je suis saturé)
Dernière modification par azizovsky ; 03/03/2016 à 21h39.

- 03/03/2016, 21h54 #45geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
DONC:
============================== =======================
POST CHECK_POINT
Reformulation claire et self-contained du problème dans l'état actuel d'avancement
============================== =======================
On cherche les composantes du vecteur :

où et
et 
 pour
pour  ,
,  <------ !!!
<------ !!!
 .
.
============================== =======================
- [#44.a]
Partant de cette nouvelle formulation beaucoup plus simple à manipuler, il vient directement:

Voilà qui est fait
On trouve donc


Et s'en suit

IS THAT RIGHT?
Dernière modification par geometrodynamics_of_QFT ; 03/03/2016 à 21h56.

- 03/03/2016, 22h01 #46geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217

- 03/03/2016, 22h03 #47invite57a1e779
- Date d'inscription
- janvier 1970
- Messages
- 9 645
Re : Somme vectorielle
Rectification des fautes de frappe :

donc elle est satisfaite au rang avec :
avec :  .
.

- 03/03/2016, 22h20 #48geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217

- 03/03/2016, 22h29 #49azizovsky
- Date d'inscription
- septembre 2010
- Messages
- 5 348
Re : Somme vectorielle
mon calcul, c'est une idée qui ma'a chiffonné, pas plus, en plus à toi l'honneur dans tous las cas ...., c'est ton problème et c'est eux qui font avancer .....
ps: dans les détails se cache le .
. , bonne soirée ....
, bonne soirée ....
Dernière modification par azizovsky ; 03/03/2016 à 22h31.

- 03/03/2016, 22h49 #50geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
Zut, j'aurais dû tout réexprimer en fonction de L...
Si on veut vraiment pouvoir garder le paramètre L, on peut écrire:
 pour
pour  ,
,  ,
, 
et

et qu'on a "résolu" (plutôt simplifié) le cas :
:


- 03/03/2016, 23h06 #51azizovsky
- Date d'inscription
- septembre 2010
- Messages
- 5 348
Re : Somme vectorielle
l'origine des vecteurs n'est pas 'l'intersection' de la spirale d'or comme cas particulier avec les carreaux ...comme ici : https://fr.wikipedia.org/wiki/Nombre..._spiral_34.svg
Dernière modification par azizovsky ; 03/03/2016 à 23h11.

- 03/03/2016, 23h44 #52azizovsky
- Date d'inscription
- septembre 2010
- Messages
- 5 348
Re : Somme vectorielle
oui j'ai oublier de dire (d'après les schèmas) que


- 04/03/2016, 00h06 #53geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
@azizovsky:
ça pourrait être flachant qu'il y ait un lien avec la spiralo d'or mais je ne crois aps que ça soit le cas ici :
déjà, le rapport des longueurs des segments n'est pas le même (or is it?)
et puis, ça ne correspondrait qu'au cas particulier .
.
En cette valeur de , aucune courbe n'est présente dans le problème.
, aucune courbe n'est présente dans le problème.
Et si on parle éventuellement des arcs de cercle orange, a) ils ont une dérivée discontinue aux coudes (car issus de cercles de rayons décrémentant discrètement et dont les centres ne sont pas alignés sur le rayon du précédent (cfr F(x)) b) ils tendent vers des segments de droites pour , donc ne forment pas une spirale continue...
, donc ne forment pas une spirale continue...
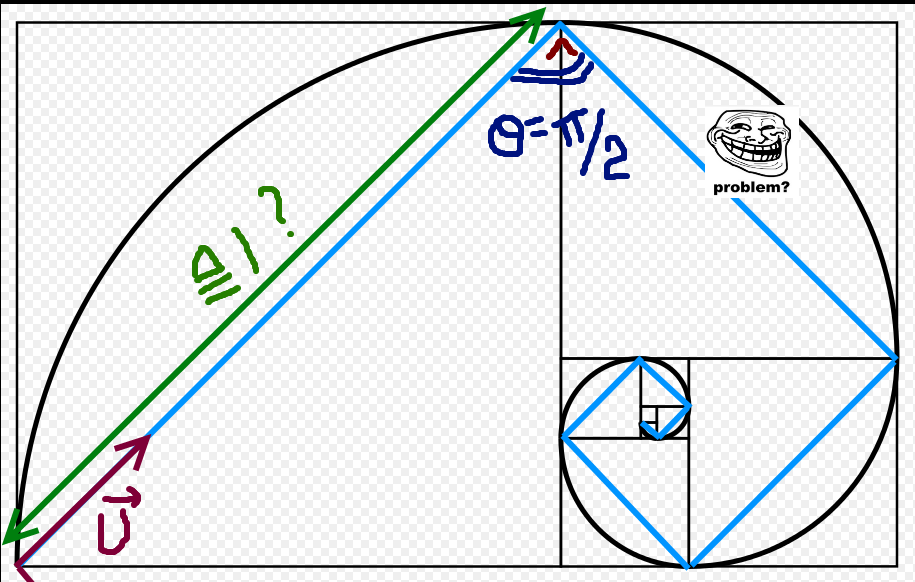
Dernière modification par geometrodynamics_of_QFT ; 04/03/2016 à 00h09.

- 04/03/2016, 01h24 #54geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
Haha excellent :
pour , on a
, on a

Et là, la devient marrant :
- si
 alors:
alors:

- si
 est pair alors
est pair alors 
- si
 est impair alors
est impair alors 
- si
- si
 alors:
alors:

- si
 est pair alors
est pair alors  (n=1,5,9, ...)
(n=1,5,9, ...) - si
 est impair alors
est impair alors  (n=3,7,11, ...)
(n=3,7,11, ...)
- si
Il faudrait vérifier tout ça, mais dans ce cas, après beaucoup de chipotage, j'ai finalement joyeusement trouvé :

De manière incroyable et magique, AUCUNE composante imaginaire ne surgit, elles s'annulent toute au sein de leur propre terme, et c'est normal, car on travaille dans le plan réel lol.
Mais c'est dingue de voir ça en vrai...
Enfin..toujours à vérifier...
quelqu'un pour confirmer?
prochaine étape: séparer les composantes u et v, et travailler explicitement sur les 2 suites en parallèle, j'imagine...
Par exemple

Dernière modification par geometrodynamics_of_QFT ; 04/03/2016 à 01h29.

- 04/03/2016, 02h12 #55geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
Donc pour terminer le raisonnement:

et
 ...
...
Un erreur quelque part??Dernière modification par geometrodynamics_of_QFT ; 04/03/2016 à 02h14.

- 04/03/2016, 09h40 #56azizovsky
- Date d'inscription
- septembre 2010
- Messages
- 5 348
Re : Somme vectorielle
pour



pour


Dernière modification par azizovsky ; 04/03/2016 à 09h44.

- 04/03/2016, 09h46 #57gg0Animateur Mathématiques
- Date d'inscription
- avril 2012
- Âge
- 76
- Messages
- 31 351
Re : Somme vectorielle
Heu ... Azizivsky,
ta série géométrique a une valeur facile à calculer ... 2/3.
Cordialement.
- 04/03/2016, 09h49 #58azizovsky
- Date d'inscription
- septembre 2010
- Messages
- 5 348

- 04/03/2016, 13h29 #59geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217
Re : Somme vectorielle
 ??????
??????
quid en pi/2, où on voit que le point converge dans l'intervalle ( [0,1], [1,2] ) ????
sinon, azizovsky et gg0 : (message #9 de ce fil)
où je parlais en fait de ...
...
Dernière modification par geometrodynamics_of_QFT ; 04/03/2016 à 13h33.

- 04/03/2016, 13h35 #60geometrodynamics_of_QFT
- Date d'inscription
- décembre 2014
- Messages
- 1 217

Discussions similaires
-
Module d'une somme vectorielle.
Par invite92fdbd33 dans le forum Mathématiques du collège et du lycéeRéponses: 12Dernier message: 10/10/2014, 20h53 -
Convergence et limite de la somme d'une somme [séries]
Par invite3acfbda2 dans le forum Mathématiques du supérieurRéponses: 17Dernier message: 16/10/2009, 10h17 -
Déterminer le taux d'intérêt à partir de la somme investie et de la somme de fin de placement ?
Par Myr dans le forum Mathématiques du supérieurRéponses: 1Dernier message: 11/07/2009, 17h39 -
Projection de somme vectorielle sur deux axes
Par invite03c3d1e5 dans le forum PhysiqueRéponses: 11Dernier message: 04/01/2008, 22h55 -
projection de somme vectorielle
Par invite56269a05 dans le forum PhysiqueRéponses: 2Dernier message: 01/01/2008, 15h32
Fuseau horaire GMT +1. Il est actuellement 05h18.

