un petit problème pour les vacances

[Liet Kynes]

Les résultats sont totalement pertinents puisqu'ils répondent à la question de MissJenny.
Tu peux poser une autre question,mais alors il faut que tu commences à compter les pavages à demi-tour près. Et ça, ça n'a pas l'air coton. Peut-être en examinant attentivement la démonstration de la formule de comptage de pavages ?

En fait regardant bien mes deux tableaux je trouve que c'est pas si idiot ce que j'ai fait.
-----

[Biname]

@GBZM : #49 mon deuxième message, juste après l'annonce du résultat :
fichier modifié pour la postérité

• GBZM #49 13-20:48 difficile dénombrement, après yakade, code SageMath OK (traduction en python #53 13-21:52)

Biname : 201292564878142083 moi: 201292564878142304 ...083 >> ...304 +221 18 chiffres significatifs. ???
Je compte simplement les chiffres significatifs. Il suffit probablement de demander à GPT d'augmenter la précision !(1)

Merci pour le code python. J'ai dû le modifier pour qu'il marche :
Oui, il ne 'compilait' pas ici non plus(omega), correction GPT:

 Cliquez pour afficher

from sympy import symbols, sqrt, chebyshevt, I
from sympy.polys.polytools import resultant

def Pavbis(n):
    x = symbols('x')
    chebyshev_8 = chebyshevt(8, I * x / 2)
    chebyshev_n = chebyshevt(n, x / 2)
    result = sqrt(abs(resultant(chebyshev_8, chebyshev_n)))
    return result

compilait, mais les résultats n'étaient pas bons ? Faudrait que j'aille lire Tchebychev ... pfff (1).
Mes souvenirs le prénommait Binamé, faut se méfier des souvenirs : inégalité de Bienaymé-Tchebychev ? Pafnouti Tchebychev.
C'est piégé comme Stefan Boltzmann Ludwig et la loi de Stefan-Boltzmann .

GBZM : Ça déconne à partir de 17 lignes, et de plus en plus après.
OSEF un peu, c'est juste une question de précision, j'ai récemment joué avec des entiers de 2000 chiffres ? Oui, les fonctions H, SHA ... et la crypto.

As tu remarqué la magnifique demi pyramide que font les resultats notre_pb(0 à 19L, 8C)

 Cliquez pour afficher

''' GBZM
P(8,7) = 463733/1292697
n lignes et 8 colonnes, où n varie de 0 à 19 :
0,
1,
1,
67,
272,
5426,
34168,
463733,
3558245,
40423745,
341774922,
3543203530,
31430594248,
310092581147,
2815096255711,
27009936374613,
247773142270344,
2338769967876768,       moi:   2338769967876770  ...768 >> ...770    +2
21540614004729318,      moi:  21540614004729320  ...318 >> ...320    +2
201292564878142083      moi: 201292564878142304  ...083 >> ...304  +221
Ça te permettra de vérifier tes calculs. 
Format csv
  i,         sans_routes,         avec_routes,   proba,       pav possibles
  0,                   0,                   0,  1.0000,                   1
  1,                   0,                   1,  1.0000,                   1
  2,                  33,                   1,  0.0294,                  34
  3,                  86,                  67,  0.4379,                 153
  4,                1973,                 272,  0.1212,                2245
  5,                9398,                5426,  0.3660,               14824
  6,              132921,               34168,  0.2045,              167089
  7,              828964,              463733,  0.3587,             1292697
  8,             9430571,             3558245,  0.2739,            12988816
  9,            68012000,            40423745,  0.3728,           108435745
 10,           689376319,           341774922,  0.3314,          1031151241
 11,          5397536294,          3543203530,  0.3963,          8940739824
 12,         51310411581,         31430594248,  0.3799,         82741005829
 13,        421071672686,        310092581147,  0.4241,        731164253833
 14,       3860401981419,       2815096255711,  0.4217,       6675498237130
 15,      32544264094500,      27009936374613,  0.4535,      59554200469113
 16,     292288144266578,     247773142270344,  0.4588,     540061286536922
 17,    2502340065789280,    2338769967876770,  0.4831,    4841110033666050
 18,   22212118568369040,   21540614004729320,  0.4923,   43752732573098360
 19,  191846580248680992,  201292564878142304,  0.5120,  393139145126823296
'''

pour C=8

Biname

[Biname]

En fait regardant bien mes deux tableaux je trouve que c'est pas si idiot ce que j'ai fait.

Ton tableau OK, procède exactement de la même façon que ma méthode. Sans utiliser la récurrence ????
Pourrais-tu l'expliquer ? Lire les formules dans Excel est lourd
Biname

[GBZM]

Où l'on voit que ChatGPT n'est pas éduqué à faire la différence entre polynôme de Thchebychev de 1e espèce et de 2nde espèce. Même pour la traduction de code,, il vaut mieux se méfier !

[Biname]

GPT une minute :
python mpmath, nombre de décimales variables, ici 100
mpmath.sqrt(2) = 1.4142135623730950488016887242 096980785696718753769480731766 797379907324784621070388503875 34327641573
ici 200
1.4142135623730950488016887242 096980785696718753769480731766 797379907324784621070388503875 343276415727350138462309122970 249248360558507372126441214970 999358314132226659275055927557 999505011527820605715

import mpmath

mpmath.mp.dps = 100  # Changer la précision (nombre de décimales)

result = mpmath.sqrt(2)
print(result)

Réponse GPT

 Cliquez pour afficher

mpmath_128.jpg
Listes des opération mpmath npn basiques :
mpmath_op.jpg

Biname

[Liet Kynes]

Ton tableau OK, procède exactement de la même façon que ma méthode. Sans utiliser la récurrence ????
Pourrais-tu l'expliquer ? Lire les formules dans Excel est lourd
Biname

Pour chaque rectangle avec un nombre de lignes de n=2 à n=7 je cherche les combinaisons avec ligne traversantes possibles.

Initialisation: Pour n=2, il y en a qu'une car si une ligne est traversante l'autre aussi.

Pour n=3 il y a 3 combinaisons qui peuvent contenir des lignes traversantes:

- ligne 1 traversantes, 2 et 3 non traversantes (T),
- ligne 3 traversantes, 1 et 2 non traversantes,
- lignes 1,2 et 3 traversantes.

Si 1 et 2 sont non T, comme je sais que dans le rectangle de 2*8 il n'y a qu'un cas de traversante parmi 34 pavages, il reste logiquement 34-1=33 pavages sans traversantes qui se combinent avec un cas T=33*1=33
Si 2 et 3 sont non T, comme je sais que dans le rectangle de 2*8 il n'y a qu'un cas de traversante parmi 34 pavages, il reste logiquement 34-1=33 pavages sans traversantes qui se combinent avec un cas T=33*1=33
Si 1,2 et 3 sont T alors il n'y a qu'un cas qui ne se combine pas avec des non T
-> 33+33+1=67 pavages possibles avec traversante dans le rectangle n=3 (ce que je discute car pour moi les deux cas symétriques sont un et un seul)

Pour le rectangle n=4

- Ligne 1 T et 2,3,4 non T, comme je sais d'avec le calcul précédent que le rectangle 3*8 il y a 67 T parmi 153 pavages il reste logiquement 153-67=86pavages sans traversantes qui se combinent avec un cas T=86*1=86
- Ligne 4 T et 1,2,3 non T,comme je sais d'avec le calcul précédent que le rectangle 3*8 il y a 67 T parmi 153 pavages il reste logiquement 153-67=86pavages sans traversantes qui se combinent avec un cas T=86*1=86
- Lignes 1 et 2 T, 3,4 non T, comme je sais que dans le rectangle de 2*8 il n'y a qu'un cas de traversante parmi 34 pavages, il reste logiquement 34-1=33 pavages sans traversantes qui se combinent avec un cas T=33*1=33
- Lignes 3 et 4 T, 1,2 non T, comme je sais que dans le rectangle de 2*8 il n'y a qu'un cas de traversante parmi 34 pavages, il reste logiquement 34-1=33 pavages sans traversantes qui se combinent avec un cas T=33*1=33, comme je sais que dans le rectangle de 2*8 il n'y a qu'un cas de traversante parmi 34 pavages, il reste logiquement 34-1=33 pavages sans traversantes qui se combinent avec un cas T=33*1=33
- Lignes 1 et 4 T et 2,3 non T,
- Lignes 1,2,3 et 4 T, Si 1,2,3 et 4 sont T alors il n'y a qu'un cas qui ne se combine pas avec des non T.

(86*2)+(33*3)+1= 272

Et ainsi de suite jusqu'à n=7, pour les cas duals (ex : 1T,2 et 3 non T avec 3T, 1 et 2 non T) j'ai mis un coefficient de 2.
Les reports des valeurs trouvées en cours de route permettent de calculer les nouveaux rectangles.

[Biname]

Mon code python mpmath floats 32 décimales avec_routes[1 to 23, 8]
juste remplacé
import numpy as np par import mpmath as np et ajouté
np.mp.dps = 32 # Changer la précision (nombre de décimales)

 Cliquez pour afficher

Grille(8,23)    pav_possibles=2589464895903294291968
   pav_sans_routes=1122872089237874802688  pav_avec_routes=1466592806665419489280
   probalilité au moins une route = 0.5664

Temps de calcul et print 59.039817333221436 secondes


 Format csv
  i,         sans_routes,         avec_routes,   proba,       pav possibles
  0,                   0,                   0,  1.0000,                   1
  1,                   0,                   1,  1.0000,                   1
  2,                  33,                   1,  0.0294,                  34
  3,                  86,                  67,  0.4379,                 153
  4,                1973,                 272,  0.1212,                2245
  5,                9398,                5426,  0.3660,               14824
  6,              132921,               34168,  0.2045,              167089
  7,              828964,              463733,  0.3587,             1292697
  8,             9430571,             3558245,  0.2739,            12988816
  9,            68012000,            40423745,  0.3728,           108435745
 10,           689376319,           341774922,  0.3314,          1031151241
 11,          5397536294,          3543203530,  0.3963,          8940739824
 12,         51310411581,         31430594248,  0.3799,         82741005829
 13,        421071672686,        310092581147,  0.4241,        731164253833
 14,       3860401981419,       2815096255711,  0.4217,       6675498237130
 15,      32544264094500,      27009936374613,  0.4535,      59554200469113
 16,     292288144266577,     247773142270344,  0.4588,     540061286536921
 17,    2502340065789280,    2338769967876768,  0.4831,    4841110033666048
 18,   22212118568368964,   21540614004729316,  0.4923,   43752732573098280
 19,  191846580248680896,  201292564878142080,  0.5120,  393139145126822976
 20,     1691579703538198784,     1855493875024049408,  0.5231,     3547073578562248192
 21,    14684045654338134016,    17226342589098684416,  0.5398,    31910388243436818432
 22,   128981026055615610880,   158684080870617219072,  0.5516,   287665106926232829952
 23,  1122872089237874802688,  1466592806665419489280,  0.5664,  2589464895903294291968

Le temps de calcul double lorsqu'on incrémente L max. Ici 59 secondes pour ce résultats
Sauf erreursss
Biname

[gg0]

Bonjour Biname.

"inégalité de Bienaymé-Tchebychev ?". Trouvée dans des contextes différents par Jules Bienaymé, inspecteur des finances français et son ami Panofti Tchebycheff dont Bienaymé a été le traducteur en français. Mais rien à voir avec les "polynômes de Tchebycheff".

Cordialement.

[Biname]

Liet #156,
C'est la solution par récurrence de mon msg #37.

Grille(7L, 8C)
            nombre de lignes  0  1   2    3     4      5       6        7
Nombre de pavages de 0 à 7 : [0, 1, 34, 153, 2245, 14824, 167089, 1292697]
sans_lignes_list  de 0 à 7 : [0, 0, 33,  86, 1973,  9398, 132921,  828964]
avec_lignes_list  de 0 à 7 : [0, 1,  1,  67,  272,  5426,  34168,  463733]
pavage[1] = sans[i] + avec[i]

Si on ne se trompe pas, par récursion ça fonctionne.
Biname

[Biname]

Bonjour Biname.
"inégalité de Bienaymé-Tchebychev ?". Trouvée dans des contextes différents par Jules Bienaymé, inspecteur des finances français et son ami Panofti Tchebycheff dont Bienaymé a été le traducteur en français. Mais rien à voir avec les "polynômes de Tchebycheff".
Cordialement.

Je m'étais z_a_p_l_i_k_é à recopier son prénom https://fr.wikipedia.org/wiki/Pafnouti_Tchebychev et avait pensé a la loi de Paf-Lechien à joindre aux deux précédentes.

Oui, j'ai vu passer ses filtres aussi.

Biname

[Liet Kynes]

Liet #156,
C'est la solution par récurrence de mon msg #37.

Grille(7L, 8C)
            nombre de lignes  0  1   2    3     4      5       6        7
Nombre de pavages de 0 à 7 : [0, 1, 34, 153, 2245, 14824, 167089, 1292697]
sans_lignes_list  de 0 à 7 : [0, 0, 33,  86, 1973,  9398, 132921,  828964]
avec_lignes_list  de 0 à 7 : [0, 1,  1,  67,  272,  5426,  34168,  463733]
pavage[1] = sans[i] + avec[i]

Si on ne se trompe pas, par récursion ça fonctionne.
Biname

La grande question est de savoir si le nombre total de pavages calculé par la formule comprend ou non des pavages réversibles, si ce n'est pas le cas alors il faut corriger le calcul du nombre de pavages avec lignes.

Pavages réversibles: par exemple le pavage avec uniquement ligne 1 traversante est compté mais aussi celui avec uniquement ligne 7 traversante

[Biname]

Liet msg 161,
Msg #72, mon essai de comptage des cas possibles pour une grille L=3 C=4 ne m'a présenté que 9 cas.
Avec de vrais grilles, on trouve les cas manquants :

 Cliquez pour afficher

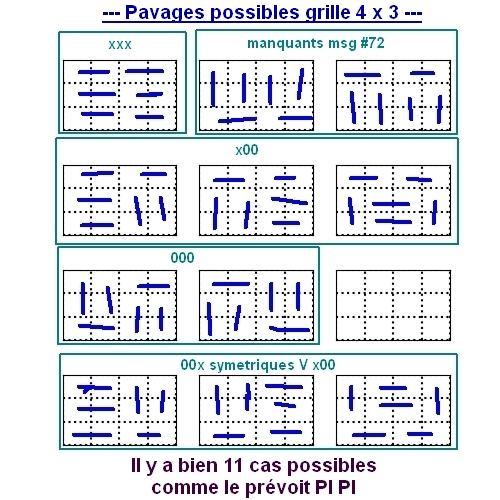
On a donc bien 11 cas possibles pour L3 * C4 ce que prévoit PI PI

Code python qui crée des grilles jpg, png et pdf

 Cliquez pour afficher

import matplotlib.pyplot as plt

def draw_dotted_grid(ax, rows, cols):
    for i in range(rows + 1):
        ax.plot([-0.5, cols - 0.5], [i - 0.5, i - 0.5], color='black', linestyle='dotted')
    for j in range(cols + 1):
        ax.plot([j - 0.5, j - 0.5], [-0.5, rows - 0.5], color='black', linestyle='dotted')
    ax.set_xticks([])
    ax.set_yticks([])
    ax.set_xlim(-0.5, cols - 0.5)
    ax.set_ylim(-0.5, rows - 0.5)

def tile_grid(rows, cols):
    grid = [[0] * cols for _ in range(rows)]
    for i in range(0, rows, 2):
        for j in range(0, cols, 2):
            grid[i][j] = 1
            grid[i+1][j] = 1
            grid[i][j+1] = 1
            grid[i+1][j+1] = 1
    return grid

rows = 3
cols = 4

fig, axs = plt.subplots(4, 3, figsize=(5, 5))   # 4 grilles H, 3 griles V  (5,5) taille de l'image
fig.subplots_adjust(hspace=0.5)

for ax in axs.flat:
    draw_dotted_grid(ax, rows, cols)

# Sauvegarder l'image aux formats JPG, PNG et PDF
plt.savefig('grid_image.jpg', format='jpg')
plt.savefig('grid_image.png', format='png')
plt.savefig('grid_image.pdf', format='pdf')

plt.show()

Biname

[Liet Kynes]

On obtiens donc des résultats variables en fonction de la manière de dénombrer les pavages.
On peut choisir de dénombrer sans tenir compte du sens du pavage -> ce que l'on a fait

Si on tiens compte du sens, les résultats sont différents:

[Liet Kynes]

Oups, 8/11=0.72 et pas 0.54

[GBZM]

On doit bien préciser ce que l'on compte. Les symétries du rectangle dépendent de si l'on demande la préservation ou non de l'orientation du plan.
Si on le demande, les seules symétries sont l'identité et le demi-tour (groupe isomorphe à Z/2Z)
Si on autorise les symétries qui renversent l'orientation, on a en plus le miroir horizontal et le miroir vertical (et le groupe des symétries est alors isomorphe à Z/2Z x Z/2Z).
Bien sûr avec un carré on a plus de symétries ; le groupe des symétries est le groupe diédral D_4 à huit éléments.

Ce que l'on compte dans tous les cas, ce sont les orbites de l'ensemble des pavages sous l'action du groupe des symétries. On a un outil classique pour ça qui est la formule de Burnside ; mais je doute qu'elle soit d'un usage facile ici.

[GBZM]

Euh, Liet Kynes, le pavage avec trois chemins traversants horizontaux n'est pas traversant ?

[Biname]

Tu nous pièges ? 9/11, tu as mal compté les cas.

Maintenant qu'on sait que nos cas peuvent se représenter par la chaine d'un nombre binaire allant de 0 à , en scannant ces nombres en commençant par 0, le symétrique de N_bin_str est mirror_V(N_bin_str), si mirror_V(N_bin_str)) != N_bin_str alors check(Mirror(N_bin_str) = false, ainsi, les symétriques non égaux à eux mêmes sont sortis de la liste.

C'est simple à implémenter ... surtout en assembleur.

Depuis quelques jours, je me pose cette question : est-ce que la théorie des ensembles ne pourrait pas être réécrite avec des opérations logiques ?
E={a_0, a_1, ... , a_n} peut toujours? être réécrit E = [a(0), a(1), ..., a(n)] en faisant a(n) = a_n
à partir de là on manipule les n ... ça a dû être fait, au moins en partie ?

Pour notre crible, le point de vue numérique est bien plus simple :
On scanne les éléments des ensembles, si l'élément n'a jamais été rencontré, on l'ajoute à la liste, le boulot terminé la liste est l'union des ensembles et sa longueur son cardinal ... pour n fini. Pratiquement, il n'y a pas d'autre solution.

Biname

[Liet Kynes]

Oula-oups, j'ai fait cela avant le café du matin..

Voilà la correction :

[GBZM]

Ton code couleur ne respecte pas les symétries pour ton pavages qui a quatre versions différentes par les symétries du rectangle.
Par ailleurs tu n'indiques pas les miroirs horizontaux (qui échangent la gauche et la droite). Ici ça va, mais pour le cas de quatre lignes tu en auras besoin.

[GBZM]

"est-ce que la théorie des ensembles ne pourrait pas être réécrite avec des opérations logiques ?"
Biname, ce que tu appelles théorie des ensembles, c'est les propriétés de l'union, de l'intersection, du passage au complémentaire ? Ce n'est pas la théorie des enesembles des matheux. Mais bien sûr ça a tout à voir avec les connecteurs logiques OU, ET et NON.

[Liet Kynes]

Les couleurs ne servent pas à grand-chose, pour la grille 4*3 il y a bien une rotation dans les deux axes pour une des figures: les petites flèches qui forment une croix sont mal disposées:
-> corrections effectuées :

[GBZM]

"les petites flèches qui forment une croix sont mal disposées:"
Non, puisqu'il y a bien une symétrie centrale (ou demi-tour). Remarque qu'il peut y avoir des pavages qui présentent une symétrie centrale, mais ni miroir horizontal ni miroir vertical.
"une rotation dans les deux axes" ???
Ni le miroir horizontal ni le miroir vertical ne sont des rotations

[Biname]

"est-ce que la théorie des ensembles ne pourrait pas être réécrite avec des opérations logiques ?"
Biname, ce que tu appelles théorie des ensembles, c'est les propriétés de l'union, de l'intersection, du passage au complémentaire ? Ce n'est pas la théorie des enesembles des matheux. Mais bien sûr ça a tout à voir avec les connecteurs logiques OU, ET et NON.

Dans mon " Pratiquement, il n'y a pas d'autre solution.", pour un matheux, il y a un mot de trop .

Biname

[Liet Kynes]

"les petites flèches qui forment une croix sont mal disposées:"
Non, puisqu'il y a bien une symétrie centrale (ou demi-tour). Remarque qu'il peut y avoir des pavages qui présentent une symétrie centrale, mais ni miroir horizontal ni miroir vertical.
"une rotation dans les deux axes" ???
Ni le miroir horizontal ni le miroir vertical ne sont des rotations

Je raisonne en imaginant que mon pavage est une feuille translucide que je tourne vers la droite ou la gauche ou ver le haut ou le bas, je peux la tourner une fois vers la droite puis vers le haut ou le bas.
Bref à un pavage correspond au plus 4 dispositions, non ?

[Biname]

"les petites flèches qui forment une croix sont mal disposées:"
Non, puisqu'il y a bien une symétrie centrale (ou demi-tour). Remarque qu'il peut y avoir des pavages qui présentent une symétrie centrale, mais ni miroir horizontal ni miroir vertical.
"une rotation dans les deux axes" ???
Ni le miroir horizontal ni le miroir vertical ne sont des rotations

En 3D oui.
Biname

[Liet Kynes]

Pour trouver que n pavages sont identiques dans un ensemble de pavages défini par une grille n*m, j'ai mis au point un petit truc qui est, à confirmer, pas réalisable mais interessant à mes yeux:
On numérote chaque case de domino de la même façon et on les nombres sont attribués dans l'ordre de rencontre ds nouveaux dominos en commencant en haut à gauche à la ligne 1. Ensuite on effectue la somme des colonnes et la somme des lignes puis le produit des sommes de colonnes et le produit des sommes des lignes.

Hypothèse:
Si un pavage obtient un des produits "lignes" ou "colonne" identique à ceux d'un ou plusieurs autres, alors ces pavages sont miroirs.

[Merlin95]

Je viens de voir cette discussion.

Mais, je ne dois pas être bien malin car je n'ai pas compris le problème puisque les images restent incompréhensibles pour moi.

En effet, je pensais qu'aux dominos, si on en pose un avec le nombre , l'adversaire suivant doit mettre à coté aussi un domino avec le même nombre . Sinon il pioche.

Mais je ne vois pas cette règle appliquée dans les images des premiers messages (sauf erreur).

[Liet Kynes]

Je viens de voir cette discussion.

Mais, je ne dois pas être bien malin car je n'ai pas compris le problème puisque les images restent incompréhensibles pour moi.

En effet, je pensais qu'aux dominos, si on en pose un avec le nombre , l'adversaire suivant doit mettre à coté aussi un domino avec le même nombre . Sinon il pioche.

Mais je ne vois pas cette règle appliquée dans les images des premiers messages (sauf erreur).

Il s'agit du jeu dominosa https://fr.puzzle-dominosa.com/ (règles à gauche de la fenêtre)

[Biname]

@Merlin, msg #177
Miss Jenny :
msg #1 : "En supposant que toutes les configurations sont équiprobables, peut-on calculer la probabilité qu'il y ait au moins une traversée rectiligne?"
msg #5 : "on peut oublier les chiffres inscrits sur les dominos. Il s'agit de paver le tableau de 8*7 cases avec des rectangles qui couvrent deux cases, et qui peuvent être disposés verticalement ou horizontalement. Je ne sais pas combien il y a de configurations. Pas mal sans-doute..."

Biname msg #26
"si on ajoute :
- le nombre de colonnes doit être pair
- on parle de routes horizontales uniquement
- aucune case ne peut rester vide
- aucune autre règle de pavage que 'remplir' avec des dominos 1x2"

Biname

[Merlin95]

Ok si j'ai bien compris, il s'agit d'étudier les pavages d'une grille rectangulaire de 8x7, avec des rectangles de longueur 1x2.

Ensuite, on s'intéresse aux solutions où il y a au moins une ligne droite (toujours sans tenir compte de la régle habituelle principale du jeu de dominos).

C'est bien ça ?